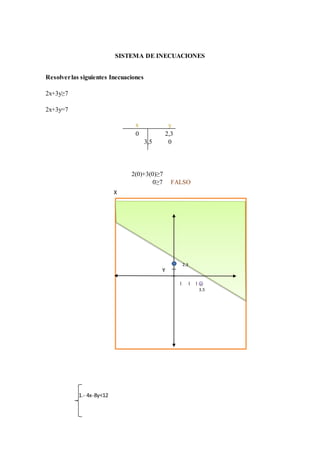
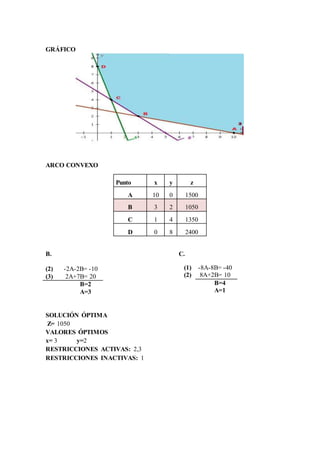
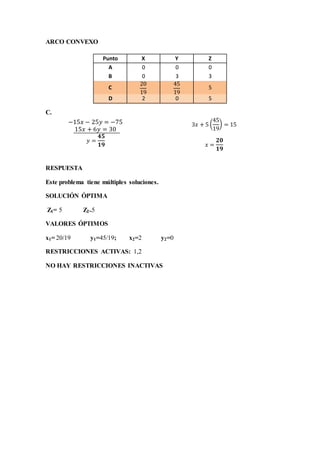
Este documento presenta 7 problemas de programación lineal resueltos. Cada problema describe una situación de optimización con restricciones y presenta tablas de datos, funciones objetivo, restricciones, sistemas de ecuaciones y gráficos para encontrar la solución óptima. Los problemas abarcan temas como maximización de beneficios, minimización de distancias y aprovechamiento de recursos bajo limitaciones.

1. SISTEMA DE INECUACIONES
Resolverlas siguientes Inecuaciones
2x+3y≥7
2x+3y=7
x y
0 2,3
3,5 0
2(0)+3(0)≥7
0≥7 FALSO
1.- 4x-8y<12
X
Y
3,5
2,3

2. 2.- 4x-8y=12
x y
0 -1,5
3 0
4(0)+8(0)<12
0<12 VERDADERO
3.-
2𝑥 − 𝑦 > 0
2𝑥 = 𝑦
x y
0 0
1 2
X
Y
3
-1,5
𝑃(2,0)
2(2) − 0 > 0
4 > 0 → Verdadero

3. 4.-
{
4𝑥2
+ 4𝑦2
≥ 36
𝑥 + 5𝑦 < 7
{
4𝑥2
+ 4𝑦2
= 36
𝑥 + 𝑦 = 7
𝑥2
+ 𝑦2
= 9
𝑃(0,0)
4(0)2
+ 4(0)2
≥ 36
0 ≥ 36 → Falso
5.-
𝟒𝒙 𝟐 + 𝟑𝒚 𝟐 < 12
𝑥 + 5𝑦 = 7
x Y
0 7
5⁄
7 0
𝑃(0,0)
0 < 7

4. 𝟐𝒙 + 𝟑 > y
𝟒𝒙 𝟐 + 𝟑𝒚 𝟐 = 12
𝑥2
3
𝑦2
4
= 1
X: √3 = 1,7
Y: √4 = 2
P(0,0)
4(02) + 3(02) <12
0 < 12 Verdadero
2x-y=-3
x y
0 3
-1,5 0
P(0,0)
2𝑥 − 𝑦 > -3
2(0)-(0) >-3
0>--3 Verdadero

5. 6. 3x2+y>6
2x2-y2<4
COMPROBACIÓN
P(0,0) P(0,0)
(1) (2)
3(0)2+(0)>6 2(0)2-(0)2<4
0>6 0<4
FALSO VERDAD
GRÁFICO
(1) (2)
3x2+y=6
y=6-3x2
2x2-y2=4
𝑥 = ±√
4 + 𝑦2
2
x y x y
-3 -21 ±2.6 -3
-2 -6 ±2 -2
-1
0
1
2
3
3
6
3
-6
-21
±1.6
±1.4
±1.6
±2
±2.6
-1
0
1
2
3

7. PROGRAMACIÓN LINEAL
1.- Una Compañía de Auditores se especialista en preparar liquidaciones y auditorías de
pequeñas empresas. Tiene interés en saber cuántas auditorías y liquidaciones pueden
realizarse mensualmente para maximizar sus ingresos? Se dispone de 600 horas de
trabajo directo y 220 horas para revisión, además aporta un ingreso de $250, una
liquidación de impuestos requiere de 6 horas de trabajo directo y 4 de revisión producen
un ingreso de $90, una auditoría requiere de 30 horas de trabajo directo y 8 de revisión,
aporta con un ingreso de $250. El máximo de liquidaciones posibles es de 50.
TABLA DE DATOS
DESCRIPCIÓN TRABAJO
DIRECTO
REVISIÓN INGRESOS MÁXIMO
LIQUIDACIONES 8 2 90 50
AUDITORÍAS 1 1 250
DISPONIBILIDAD 600 220
FUNCIÓN OBJETIVO.
Max. Z=90x+250y
RESTRICCIONES
(1) 6x+30y≤ 600
(2) 4x+8y≤ 200
(3) x≤50
RESTRICCIONES DE NO NEGATIVIDAD
(4) x,y0
SISTEMAS ECUACIONES
(1) (2) (3)
6x+30y=600 4x+8y=200 x=50
x y x y
100 0 0 27,5

8. COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) (2) (3)
6(0)+30(0)≤600 4(0)+8(0)≤ 200 0≤50
0≤600 0≤ 200
VERDAD VERDAD VERDAD
GRÁFICO
ARCO CONVEXO
0 20 55 0
Punto x y z
A 0 0 0
B 0 20 1050
C 25 15 6000
D 50 0 4500

9. C.
SOLUCIÓN ÓPTIMA
Z= 1050
VALORES ÓPTIMOS
x= 3 y=2
RESTRICCIONES ACTIVAS: 2,3
RESTRICCIONES INACTIVAS: 1
(1) -24x-120y= -2400
(2) 24x+48y= 1200
y=15
x=25

10. 2.- Un frutero necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzana. Dos
mayoristas pueden suministrarle para satisfacer sus necesidades pero solo venden la
fruta en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de
naranjas, 1 de plátanos y 2 de manzanas.
El mayorista B envía en cada contenedor 2 cajas de naranja, 1 de plátano y 7 de
manzanas si se sabe que el mayorista A se encuentra a 150 km de distancias y el
mayorista B a 30 km. Determine cuantos contenedores habrá que comparar a cada
mayorista con el objeto de ahorrar tiempo dinero y minimizar la distancia.
TABLA DE DATOS
DESCRIPCIÓN A B DISPONIBILIDAD
NARANJA 8 2 16
PLÁTANOS 1 1 5
MANZANAS 2 7 20
DISTANCIA 150 30
FUNCIÓN OBJETIVO.
Min. Z=150x+30y
RESTRICCIONES
(1) 8x+2y16
(2) x+y5
(3) 2x+7y20
RESTRICCIONES DE NO NEGATIVIDAD
(4) x,y0
SISTEMAS ECUACIONES
(1) 8x+2y=16 (2) x+y=5 (3) 2x+7y=20
COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) 8(0)+2(0)16 (2) 0+05 (3) 2(0)+7(0)20
016 05 020
FALSO FALSO FALSO
x y
0 8
2 0
x y
0 5
5 0
x y
0 2,9
10 0

11. GRÁFICO
ARCO CONVEXO
B. C.
(2) -2A-2B= -10
(3) 2A+7B= 20
B=2
A=3
SOLUCIÓN ÓPTIMA
Z= 1050
VALORES ÓPTIMOS
x= 3 y=2
RESTRICCIONES ACTIVAS: 2,3
RESTRICCIONES INACTIVAS: 1
Punto x y z
A 10 0 1500
B 3 2 1050
C 1 4 1350
D 0 8 2400
(1) -8A-8B= -40
(2) 8A+2B= 10
B=4
A=1

12. 3.- MAXIMIZAR
FUNCIÓN OBJETIVO
𝑍 =
5
2
𝑥 + 𝑦
SUJETO A
(1) 3𝑥 + 5𝑦 ≤ 15
(2) 5𝑥 + 2𝑦 ≤ 10
CONDICIONES TÉCNICAS
𝑥 ≥ 0 O 𝑗 = 1; 2
GRÁFICO
(1) (2)
3x+5y=15 5x+2y=10
x y
0 3
5 0
0 ≤ 15
x y
0 5
2 0
0 ≤ 10

13. ARCO CONVEXO
C.
RESPUESTA
Este problema tiene múltiples soluciones.
SOLUCIÓN ÓPTIMA
Z1= 5 Z2=5
VALORES ÓPTIMOS
x1= 20/19 y1=45/19; x2=2 y2=0
RESTRICCIONES ACTIVAS: 1,2
NO HAY RESTRICCIONES INACTIVAS
Punto X Y Z
A 0 0 0
B 0 3 3
C
20
19
45
19
5
D 2 0 5
−15𝑥 − 25𝑦 = −75
15𝑥 + 6𝑦 = 30
𝑦 =
𝟒𝟓
𝟏𝟗
3𝑥 + 5 (
45
19
) = 15
𝑥 =
𝟐𝟎
𝟏𝟗

14. 4.- MAXIMIZAR
FUNCIÓN OBJETIVO
Z= 2x+3y
SUJETO A
(1) x≤2
(2) y≥4
(3) 2x+y≥5
CONDICIÓN TÉCNICA
(4) x,y 0
SISTEMA DE ECUACIONES
COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) (2) (3)
x≤2 y≥4 2x+y≥5
0≤2 04 05
VERDAD FALSO FALSO
GRÁFICO
(1) (2) (3)
x=2 y=4 2x+y=5 x y
0 5
5/2 0

15. ARCO CONVEXO
PUNTOS x y z
A 2 4 16
B 1/2 4 13
C 0 5 15
B.
SOLUCIÓN ÓPTIMA
Z= 16
VALORES ÓPTIMOS
x= 2 y=4
RESTRICCIONES ACTIVAS: 1,2
RESTRICCIONES INACTIVAS: 3
(3) -2x-y= -5
(2) y= 4
x=1/2
y=4

16. 5.- MAXIMIZAR
FUNCIÓN OBJETIVO
Z= 2x+3y
RESTRICCIONES
(1) x≤2
(2) y≤3
(3) 2x+y≥18
RESTICCIONES DE NO NEGATIVIDAD
(4) x+y≥0
SISTEMAS DE ECUACIONES
COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) (2) (3)
x≤2 y≤3 2x+y≥18
0≤2 0≤3 018
VERDAD VERDAD FALSO
GRÁFICO
RESPUESTA: El problema no tiene solución
x y
0 18
9 0
(1) (2) (3)
x=2 y=3 2x+y=18

17. 6.- Una compañía produce automóviles y camiones, cada vehículo tiene que pasar por
un taller de pintura y un taller de montaje de carrocería si el taller de pintura pinta
solamente camiones, se podría pintar 40 camiones al día y si pinta solo automóviles se
podrían pintar 60 automóviles si el taller de carrocerías ensamblara solo camiones
podría ensamblar 50 camiones al día y si ensamblaría solo automóviles podrían
ensamblar 50 automóviles al día cada camión aporta $300 a la utilidad y cada
automóvil $200. Maximice la utilidad.
Pintura PENDIENTE
P1(0,40) 𝑚 =
𝑦2−𝑦1
𝑥2−𝑥1
P2(60,0) 𝑚 =
40−0
0−60
𝒎 = −
𝟐
𝟑
Ensamblaje PENDIENTE ECUACIÓN DE LA RECTA
P(0,50) 𝑚 =
𝑦2−𝑦1
𝑥2−𝑥1
y-y1=m(x-x1)
P(50,0) 𝑚 =
50−0
0−50
y-50=-1 (x)
𝒎 = −𝟏 x+y=50
FUNCIÓN OBEJTIVO
Z= 200x+ 300y
RESTRICCIONES
(1) 2x+3y ≤ 120
(2) x+y ≤ 50
RESTRICCIONES DE NO NEGATIVIDAD
(3) x,y0
ECUACIÓN DE LA RECTA
y-y1=m(x-x1)
y-40=-2/3 (x)
3y-120=-2x
2x+3y=120

18. SISTEMAS DE ECUACIONES
COMPROBACIÓN
P(0,0) P(0,0)
(1) (2)
2(0)+3(0)≤120 (0)+(0)≤ 50
0≤120 0≤ 50
VERDAD VERDAD
GRÁFICO
(1) (2)
2x+3y=120 x+y=50
x y x y
60 0 0 50
0 40 50 0

19. ARCO CONVEXO
C.
RESPUESTA
El problema tiene múltiples soluciones.
SOLUCIÓN ÓPTIMA
Z1= 12000 Z2=12000
VALORES ÓPTIMOS
x1= 0 y1=40; x2=30 y2=20
RESTRICCIONES ACTIVAS: 1,2
NO HAY RESTRICCIONES INACTIVAS
Punto x y z
A 0 0 0
B 0 40 12000
C 30 20 12000
D 50 0 10000
(1) -2x-3y= -120
(2) 2x+2y= 100
y=20
x=30

20. 7.- En una pastelería se hace 2 tipos de torta. Vienesa y Real. Cada torta Vienesa
necesita ¼ de relleno por cada Kg de bizcocho y produce un beneficio de $250. Una
torta Real necesita ½ kg de relleno por cada kg de Bizcocho y produce $400 de
beneficio en la pastelería e pueden hacer diariamente hasta 150kg de bizcocho y 50kg
de relleno. Por problemas de la maquina o se pueden hacer más de 125 tortas de cada
tipo. Determine cuantas tortas de cada tipo deben venderse al día para maximizar el
beneficio.
FUNCIÓN OBJETIVO
MAX. Z= 250x + 400y
RESTRICCIONES
(1) x +y ≤ 150
(2) 0,250x + 0,500y ≤ 50
(3) X ≤ 125
(4) y ≤ 125
RESTRICCIONES DE NO NEGATIVIDAD
(5) x, y ≥ 0
SISTEMAS ECUACIONES
COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) (2) (3)
(0)+(0)≤150 0,250(0)+0,500(0)≤ 50 0≤125 VERDAD
0≤150 0≤ 50 (4)
VERDAD VERDAD 0≤125 VERDAD
(1) (2) (3) (4)
x+y=150 0,250x+0,500y=50 x=125 y=125
X y x Y
150 0 0 100
0 150 200 0

21. GRÁFICO
ARCO CONVEXO
C.
SOLUCIÓN ÓPTIMA
Z= 131200
VALORES ÓPTIMOS
x= 125 y=25
RESTRICCIONES ACTIVAS: 2,3 RESTRICCIONES INACTIVAS: 1
Punto x Y Z
A 0 0 0
B 0 100 40000
C 50 100 32500
D 125 25 131200
E 125 0 31250
(1) -0,250 x -0,250y ≤ -37,5
(2) 0,250x + 0,500y ≤ 50
y=50
x=100

22. 8.- Una joyería elaboro 2 modelos de joyas el primer modelo es 5, 5,20 y el segundo
modelo es 5, 10,5, los números que se indican representan en porcentaje oro, plata,
cobre la joyería dispone de 10kg de oro, 180 de plata y 200 kg de cobre por cada tipo de
modelo 5, 5, 10 se obtiene una utilidad de $18,50 y por el otro modelo una utilidad de
$20,00 maximice la utilidad establezca restricciones activas e inactivas y verifica si hay
holgura o excedente.
FUNCIÓN OBJETIVO
Max Z= 8,50x + 20Y
SUJETO A
(1) 0,05X + 0,05y ≤ 110
(2) 0,05x + 0,10y ≤ 180
(3) 0,10x + 0,05y ≤ 200
RESTRICCIONES DE NO NEGATIVIDAD
(4) x, y ≥ 0
SISTEMAS DE ECUACIONES
COMPROBACIÓN
P(0,0) P(0,0) P(0,0)
(1) (2) (3)
0,05(0)+0,05(0)≤110 0,05(0)+0,10(0)≤ 180 0,10(0)+0,05(0)≤200
0≤110 0≤ 180 0≤200
VERDAD VERDAD VERDAD
(1) (2) (3)
0,05X + 0,05y = 110 0,05x + 0,10y =180 0,10x + 0,05y = 200
x y x y x y
2200 0 0 1800 0 4000
0 2200 3600 0 2000 0

23. GRÁFICO
C D
(1) 0,05x + 0,05y = 110 (-1) (1) 0,05x + 0,05y = 110 (-1)
(2) 0,05x + 0,10y= 180 (2) 0,10x + 0,05y= 200
- 0,05x - 0,05y = -110 0,05x - 0,05y = -110
0,05x+ 0,10y = 180 0,10x+ 0,05y = 200
0,05 y= 70 0,05 X = 90
Y= 1400 y= 1800
0,05x + 0,10 y = 180 0,10x + 0,05 y = 200
x= 800 x= 400
Z= 18,50(800) + 20(1400) Z= 18,50(1800) + 20(400)
Z= 42800 Z= 41300
Arco Convexo Solución Óptima
X Y Z Z= 42800
C 800 1400 42800 Valores Óptimos
D 1800 400 41300 x= 800
Y= 1400
Cálculode la Holgura para el oro
0,05x + 0,05y ≤ 110
0,05(800) + 0,05(1400) + h1 ≤ 110
h1 ≤ 0 Disponibilid. Ocupados Holgura
Oro 110 110 0

24. Plata 180 180 0
Cálculode la Holgura para la plata Cobre 200 50 50
0,05x + 0,10y ≤ 180
0,05(800) + 0,10(1400) + h2 ≤ 180 Solución Óptima
h2 ≤ 0 Z= 42800
Valores Óptimos
x= 800
Cálculode la Holgura para el cobre Y= 1400
0,10x + 0,05y ≤ 200 h1= 0
0,10(800) + 0,05(1400) + h3 ≤ 200 h2= 0
h3 ≤ 50 h3= 50
Restricción Activa= 1,2
Restricción Inactiva= 3