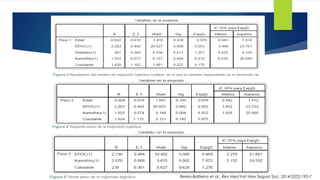
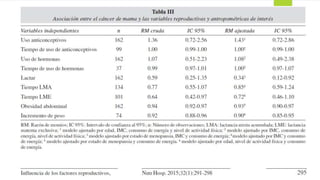
La regresión logística es un modelo utilizado en investigación clínica para predecir la probabilidad de que ocurra un evento, donde la variable dependiente es dicotómica. Las variables independientes pueden ser continuas, ordinales o dicotómicas, y la relación entre ellas debe ser clara para establecer factores de riesgo. Se recomienda realizar análisis bivariados iniciales y un modelo final que incluya variables con soporte estadístico, evitando la inclusión de variables cuya relación con la enfermedad no se conozca.






![Pasos
1er paso – hacer una análisis
bivariado con cada una de las
posibles variables involucradas
Las variables dicotómicas se
contrastan con Chi cuadrada
Las variables continuas se
contrastan con t de Student
La medida de asociación es
OR (Exp[β])
IC 95% (valor mínimo y
máximo)
Una vez identificadas las
variables que se asocian,
haremos el modelo
multivariado (preselección)
Eliminando las variables sin
relación
Eliminando las variables con
mayor p-valor
Se recomienda no eliminar
variables que tengan lógica
biológica (ej., edad) con el fin
de ajustar el modelo
Berea-Baltierra et al., Rev Med Inst Mex Seguro Soc. 2014;52(2):192-7](https://image.slidesharecdn.com/19-151010024918-lva1-app6891/85/19-Regresion-Logistica-7-320.jpg)