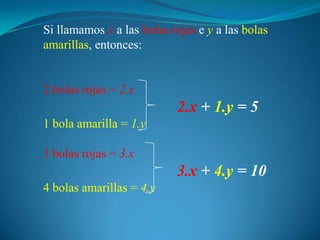
El documento describe cómo resolver un sistema de ecuaciones lineales con dos incógnitas (x e y) que representan bolas de colores. Siguiendo los pasos del método de igualación, se igualan las ecuaciones para despejar la misma incógnita, se igualan las expresiones resultantes para encontrar el valor de una incógnita, y luego se sustituye en la otra ecuación para encontrar el valor de la segunda incógnita. La solución al sistema es S=(2,1), por lo que hay 2 bolas rojas y 1 bola amarilla.

1. Sistemas de Ecuaciones lineales con dos incógnitas

2. Analiza la siguiente situación:

3. Si llamamos x a las bolas rojas e y a las bolas amarillas, entonces:2 bolas rojas = 2.x2.x+ 1.y = 51 bola amarilla = 1.y3 bolas rojas = 3.x3.x+ 4.y = 104 bolas amarillas = 4.y

4. El sistema de dos ecuaciones lineales con dos incógnitas será:2.x+ 1.y = 53.x+ 4.y = 10

5. Si resolvemos el sistema por el Método de Igualación debemos seguir los 4 pasos:1-Despejar de ambas ecuaciones la misma incógnita (a elección, preferentemente la y).2-Igualamos las expresiones que obtuvimos y resolvemos la ecuación que ahora tiene una sola incógnita.3-Se reemplaza el valor hallado (x)en una de las ecuaciones despejadas en el primer paso, obteniendo de este modo, el valor de la otra incógnita.4-La solución se escribe: S = (x ; y)

6. 2.x+ 1.y = 53.x+ 4.y = 101-Despejar de ambas ecuaciones la misma incógnita (a elección, preferentemente la y).2.x+ 1.y = 5y = 5 - 2.x3.x+ 4.y = 104.y = 10 - 3.x y = 10 - 3.x4

7. 2.x+ 1.y = 53.x+ 4.y = 102-Igualamos las expresiones que obtuvimos y resolvemos la ecuación que ahora tiene una sola incógnita. 5 - 2.x= 10 - 3.x4(5 – 2.x).4 = 10 - 3.x 20 – 8.x = 10 - 3.x – 8.x +3.x = 10 – 20 – 5.x = - 10x = - 10 : (-5) x = 2

8. 2.x+ 1.y = 53.x+ 4.y = 103-Se reemplaza el valor hallado (x)en una de las ecuaciones despejadas en el primer paso, obteniendo de este modo, el valor de la otra incógnita.y = 5 - 2.xy = 5 - 2.2y = 5 - 4y = 1

9. 2.x+ 1.y = 53.x+ 4.y = 104-La solución se escribe: S = (x ; y) S = (2 ; 1)

10. Respuesta:Las bolas rojas valen 2 puntos y las bolas amarillas valen 1 punto.

11. Fin