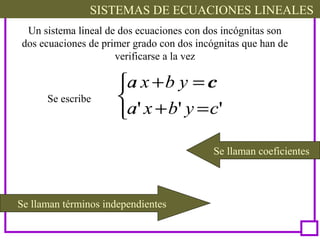
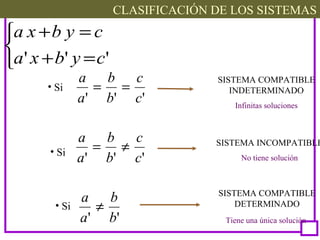
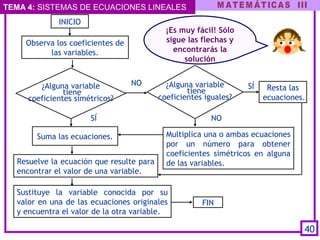
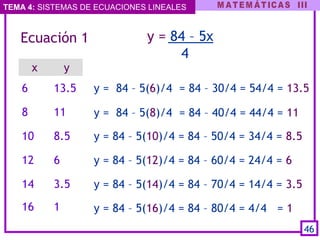
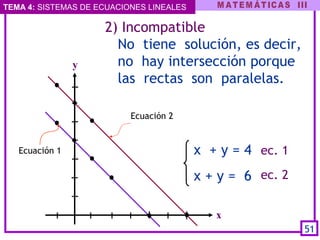
Este documento presenta el tema de los sistemas de ecuaciones lineales. Explica qué son los sistemas de ecuaciones lineales, cómo se escriben y clasifican. Luego, describe varios métodos para resolver sistemas de ecuaciones lineales, incluyendo sustitución, igualación y reducción. Finalmente, aplica estos métodos para resolver un problema de la vida real sobre los costos de cuadernos y plumones comprados.