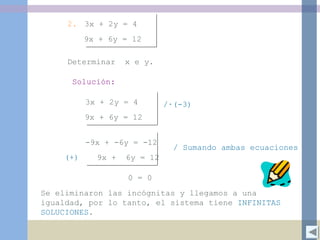
Este documento presenta conceptos sobre ecuaciones de primer grado y sistemas de ecuaciones. Explica cómo resolver ecuaciones numéricas, literales y fraccionarias, así como los métodos de igualación, sustitución y reducción para resolver sistemas de dos ecuaciones con dos incógnitas. También incluye ejemplos y ejercicios de aplicación de los temas.

1. UNIDAD 2
ÁLGEBRA
“Ecuaciones de primer grado y sistemas de ecuaciones”
Dr. Daniel Tapia Sánchez

2. • Resolver ecuaciones de primer grado con una incógnita, sean éstas numéricas,
literales o fraccionarias .
• Reconocer los métodos de resolución de sistemas de ecuaciones,
estableciendo las diferencias entre un procedimiento y otro.
• Aplicar los métodos de resolución de sistemas de ecuaciones en
problemas de planteo.
• Reconocer cuándo un sistema de ecuaciones tiene infinitas
soluciones y cuándo no tiene solución.
En esta actividad aprenderás a:

3. ContenidosContenidos
2.5 Ecuación de primer grado con una
incógnita
2.5.1 Ecuaciones numéricas
2.5.2 Ecuaciones literales
2.6 Sistemas de ecuaciones
2.6.1 Métodos de resolución
2.5.3 Ecuaciones fraccionarias
2.6.1.1 Igualación
2.6.1.1 Sustitución
2.6.1.1 Reducción

4. 2.7. Ecuación de primer grado
Es aquella, en que el mayor
exponente de la incógnita es 1 y,
por lo tanto, tiene una solución.

5. 2.7.1 Ecuaciones numéricas
Ejemplos:
a
)
5x + 10 = 2x + 22
5x - 2x +10 = 2x + 22 -2x
3x + 10 = 22
3x + 10 – 10 = 22 - 10
3x = 12
3x = 12
3 3
x = 4⇒
/ Restando 2x
/ Restando 10
/ Dividiendo por 3
4 es solución de la ecuación, es decir, al
reemplazar 4 en la ecuación, se cumple la igualdad.

6. b) 10x + 7 - 6x + 9 = 4x + 16 / Reduciendo
términos semejantes
4x + 16 = 4x + 16 / Restando 16
4x + 16 – 16 = 4x + 16 - 16
4x = 4x
Cuando en una ecuación, las incógnitas se eliminan y
se llega a una igualdad, la ecuación tiene
“INFINITAS SOLUCIONES”, es decir, para cualquier
valor de x se cumple la igualdad.
/ Restando 4x
4x – 4x = 4x – 4x
0 = 0

7. c) 8x + 2 + 3x = 9x + 12 +2x / Reduciendo
términos semejantes
11x + 2 = 11x + 12 / Restando 2
11x = 11x + 10 / Restando 11x
0 = 10
11x + 2 -2 = 11x + 12 -2
11x – 11x = 11x + 10 – 11x
Cuando en una ecuación, las incógnitas se
eliminan y
NO se llega a una igualdad, la ecuación “ NO
TIENE SOLUCIÓN”, es decir, no existe un valor
para x que cumpla la igualdad.

8. 2.7.2 Ecuaciones literales
Ejemplos:
a) px + q = qx + p / - qx
Determinar el valor de x en las siguientes
ecuaciones:
px + q – qx = qx + p - qx
px + q – qx =
p
/ - q
px + q – qx - q = p - q
px – qx = p - q / Factorizando por x
x(p– q) = p -
q
x = 1
/ Dividiendo por (p-q), con p = q.

9. b) a(x + b) = ac - ax / Multiplicando
ax + ab = ac - ax / Sumando ax
ax + ax + ab = ac - ax + ax
2ax + ab = ac / Restando ab
2ax + ab - ab = ac - ab
2ax = ac - ab / Factorizando por
a
2ax = a(c – b) / Dividiendo por 2a, con a =
0
x = (c – b)
2
2a
2ax = a(c – b)
2a

10. 2.7.3 Ecuaciones fraccionarias
Un método muy útil para resolverlas es eliminar
los denominadores y dejarlas lineales.
Ejemplo:
Determine el valor de x en la siguiente
ecuación:
.3
5
x + 3
15
= 3
10
x - 2
3
5
x + 1
5
3
10
x - 2=
3
5
x + 1
5
=
3
10
x – 10∙210∙ 10∙ 10∙
2∙3x + 2∙1 = 1∙3x - 20
6x + 2 = 3x - 20
/ Simplificando
/ Multiplicando por 10
/ Simplificando

11. 3x + 2= -20
3x = -22
3
3x = -22
3
x = -22
3
6x - 3x + 2= 3x – 3x - 20
/ Restando 2
3x + 2 - 2 = -20 - 2
/ Dividiendo por 3
6x + 2 = 3x -20 / Restando 3x

12. 2.8. Sistemas de Ecuaciones
Es un conjunto de ecuaciones donde
hay más de una incógnita.
Para determinar el valor numérico
de cada una de ellas, debe existir
la misma cantidad de ecuaciones
que de incógnitas, es decir, si
hay 3 incógnitas, debe haber 3
ecuaciones distintas.

13. 2.8.1. Métodos de resolución de un sistema
de ecuaciones de primer grado con
dos incógnitas
• Igualación:
Una vez despejada, se igualan los
resultados.
Consiste en despejar la misma incógnita
en ambas ecuaciones del sistema.
El resultado obtenido se reemplaza en
cualquiera de las ecuaciones originales del
sistema.

14. Ejemplo:
1) 2x + 3y = 7
2) x - 4y = -2
Despejando x en ambas ecuaciones:
1) 2x + 3y = 7
2x = 7 - 3y
x = 7 - 3y
2
2) x - 4y = -2
x = -2 + 4y
Igualando ambas ecuaciones:
7 - 3y
2
= -2 + 4y

15. 7 - 3y
2
= -2 + 4y
7 – 3y = -4 + 8y
7 – 3y + 3y = -4 + 8y + 3y
7 = -4 + 11y
7 + 4= -4 + 11y + 4
11= 11y
1= y
/ Multiplicando
por 2
/ + 3y
/ + 4
/ :11
Reemplazando en cualquiera de las dos
ecuaciones del sistema se determina el valor
de x.

16. x = -2 + 4y
Reemplazando y = 1 en la ecuación 2) :
x = -2 + 4 · (1)
x = -2 + 4
x = 2
La solución corresponde al punto de intersección
de 2 rectas.
Las rectas se intersectan en el punto (x,y), en
este caso,(2,1).
Si las rectas son paralelas, no existe solución.
Si las rectas son coincidentes, tiene infinitas
soluciones.

17. • Sustitución:
Consiste en despejar una incógnita de una de
las ecuaciones del sistema.
Una vez despejada, se reemplaza en la otra
ecuación, despejando la única variable que
queda.
El resultado que se obtiene se reemplaza en
cualquiera de las ecuaciones originales del
sistema.
Ejemplo:
1) 2x + 3y = 7
2) x - 4y = -2

18. Despejando x en la ecuación 2)
x = -2 + 4y
2) x - 4y = -2
Reemplazando x en la ecuación 1)
1) 2x + 3y = 7
2(-2 + 4y) + 3y = 7
-4 + 8y + 3y = 7
11y = 7 + 4
11y = 11
y = 1
Como x = -2 + 4y⇒ x = -2 + 4 ·(1)
⇒ x = 2
/ Multiplicando
/ Sumando 4
/ Dividiendo por 11

19. • Reducción:
Consiste en igualar los coeficientes de una
misma incógnita en ambas ecuaciones del
sistema
Luego, se suman o restan ambas ecuaciones, de
modo que se eliminen los términos cuyos
coeficientes se igualaron.
Ejemplo:
1) 2x + 3y = 7
2) x - 4y = -2

20. 1) 2x + 3y = 7
2) x - 4y = -2
Para eliminar x, multiplicaremos la ecuación 2) por
-2
/ · (-2)
1) 2x + 3y = 7
2)-2x + 8y = 4
/ Sumando ambas ecuaciones
(+)
11y = 11
y = 1 / Reemplazando y=1 en la ec. 2)
2) x - 4y = -2
x - 4 ·(1) = -2
x = 2
x = -2 + 4
/ Dividiendo por 11

21. Ejercicios de Aplicación
1. Se tienen canguros y koalas, si hay 55
cabezas y 170 patas, ¿cuántos canguros y
koalas hay?
Sea c: N° de canguros y k: N° de koalas
Solución:
Como los canguros tienen 2 patas y los
koalas 4, la cantidad total de patas de
canguro será 2c y el total de patas de
koala 4k.
1) c + k = 55⇒
2) 2c + 4k = 170⇒

22. Con estas dos ecuaciones se forma el siguiente
sistema de ecuaciones:
1) c + k = 55
2) 2c + 4k = 170
/·(-2)
1) -2c - 2k = -110
2) 2c + 4k = 170
/ Sumando ambas ecuaciones
(+)
2k = 60
k = 30⇒
/ Reemplazando K=30 en la ec.
1)
1) c + k = 55
c + 30 = 55 ⇒ c = 55 - 30⇒ c = 25
Por lo tanto, hay 25 canguros y 30 koalas.

23. 2. 3x + 2y = 4
9x + 6y = 12
Solución:
3x + 2y = 4
9x + 6y = 12
/·(-3)
-9x + -6y = -12
9x + 6y = 12
/ Sumando ambas ecuaciones
(+)
0 = 0
Se eliminaron las incógnitas y llegamos a una
igualdad, por lo tanto, el sistema tiene INFINITAS
SOLUCIONES.
Determinar x e y.

24. 3. Determinar: a + b + c.
a + 2b + 3c = 51
2a + 3b + c = 72
3a + b + 2c = 57 / Sumando las tres ecuaciones(+)
6a + 6b + 6c = 180
6(a + b + c) = 180
(a + b + c) = 180
6
(a + b + c) = 30
/ Factorizando por 6
/ Dividiendo por 6