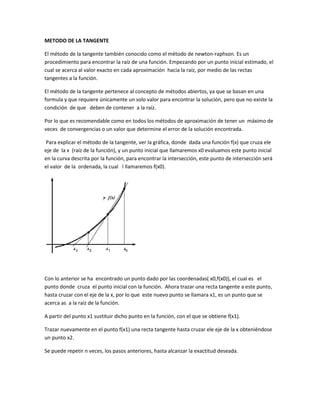
El método de la tangente, también conocido como el método de Newton-Raphson, es un procedimiento para encontrar la raíz de una función mediante el trazado de rectas tangentes. Comenzando con un punto inicial, cada aproximación se acerca más al valor real de la raíz. La fórmula generaliza este proceso para múltiples iteraciones hasta alcanzar la precisión deseada.