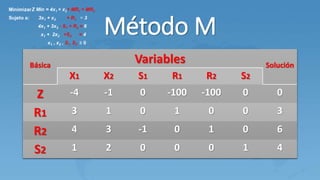
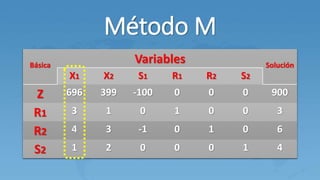
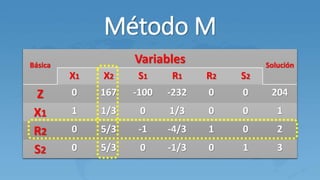
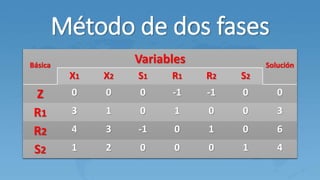
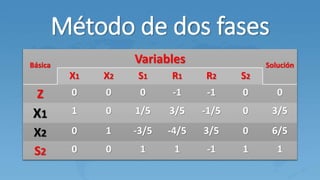
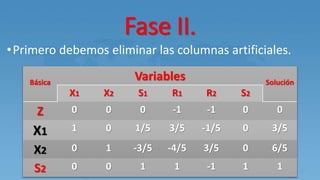
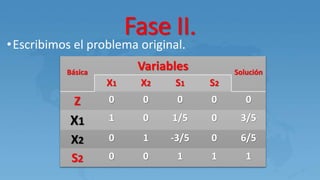
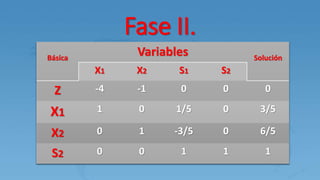
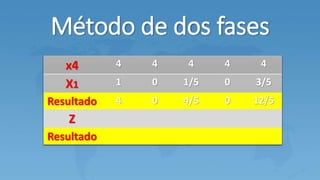
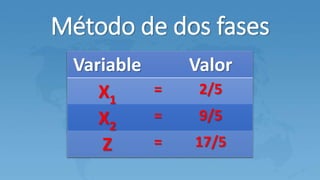
Este documento describe el método M para resolver problemas de programación lineal con variables artificiales. El método M agrega variables artificiales a las ecuaciones que no tienen holguras y penaliza estas variables en la función objetivo usando un valor M grande. Esto genera una solución básica inicial que luego se mejora a través de iteraciones del método simplex hasta eliminar las variables artificiales.

1. Unidad 2
2.3. Procedimiento para resolver problemas
con variables artificiales (M grande, doble
fase).

2. 2.3. Procedimiento para resolver problemas con
variables artificiales (M grande, doble fase).
• Las PL en las que todas las restricciones son (≤) con lados derechos
no negativos ofrecen una conveniente solución factible básica inicial
con todas las holguras. Los modelos que implican restricciones (≥) o
(=) no lo hacen. El procedimiento para iniciar PLs de “mal
comportamiento” con restricciones (≥) y (=) es utilizar variables
artificiales que desempeñan el papel de holguras en la primera
iteración, y que luego se desechan en una iteración posterior. Aquí se
presentan dos métodos estrechamente relacionados: el método M, y
el método de dos fases

3. Método M
• El método M se inicia con la PL en forma de ecuación. Si la ecuación i
no tiene una holgura (o una variable que pueda desempeñar el papel
de una), se agrega una variable artificial, Ri, para formar una
solución inicial parecida a la solución básica de total holgura. Sin
embargo, las variables artificiales no forman parte del problema
original, y se requiere un “artificio” de modelado para igualarlas a
cero en el momento en que se alcance la iteración óptima
(suponiendo que el problema tenga una solución factible). La meta
deseada se logra penalizando estas variables en la función objetivo
utilizando la siguiente regla:

4. Método M
• Regla de penalización para variables artificiales
• Dado M, un valor positivo suficientemente grande
(matemáticamente (M ∞), el coeficiente objetivo de una variable
artificial representa una penalización apropiada si:
Coeficiente objetivo de
la variable artificial
-M, en problemas de
maximización
M, en problemas de
minimización

5. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 ≥ 6
x1 + 2x2 ≤ 4
x1 , x2 ≥ 0

6. Método M
•Si utilizamos S1 como variable de superávit
en la segunda restricción y S2 como variable
de holgura en la tercera restricción, el
problema en forma de ecuación es:

7. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 ≥ 6
x1 + 2x2 ≤ 4
x1 , x2 ≥ 0

8. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 - S1 = 6
x1 + 2x2 ≤ 4
x1 , x2 ≥ 0

9. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 - S1 = 6
x1 + 2x2 +S2 = 4
x1 , x2 ≥ 0

10. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 - S1 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

11. Método M
•La tercera ecuación tiene su variable de holgura, S2,
pero la primera y segunda ecuaciones no. Por lo tanto,
agregamos las variables artificiales R1 y R2 en las
primeras dos ecuaciones y las penalizamos en la
función objetivo con MR1 + MR2 (porque estamos
minimizando). La PL resultante se da como

12. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 - S1 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

13. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

14. Método M
Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

15. Método M
Minimizar Z Min = 4x1 + x2+ R1 + R2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

16. Método M
MinimizarZ Min = 4x1 + x2+ MR1 + MR2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

17. Método M
MinimizarZ Min = 4x1 + x2+ MR1 + MR2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0
La solución básica inicial es (R1, R2, S2) = (3, 6, 4)

18. Método M
•Desde un punto de vista de cálculo, la solución del
problema con la computadora requiere que reemplace
M con un valor numérico (suficientemente grande). No
obstante, en todos los libros de texto, M se maneja
algebraicamente en la tabla simplex.

19. Método M
•El resultado es una dificultad agregada innecesaria la
cual puede evitarse sustituyendo un valor numérico
apropiado en lugar de M (lo que de cualquier modo
tenemos que hacer cuando usamos la computadora).
Nos apartamos de la larga tradición de manejar M
algebraicamente y utilizar una sustitución numérica en
su lugar. La intención es, desde luego, simplificar la
presentación sin perder la esencia.

20. Método M
•¿Qué valor de M debemos utilizar? La respuesta
depende de los datos de la programación original.
Recordemos que la penalización M debe ser lo
bastante grande con respecto a los coeficientes
objetivos originales para forzar a las variables originales
a ser cero en la solución óptima.

21. Método M
•Al mismo tiempo, como las computadoras son la
herramienta principal para resolver PLs, no es
conveniente que M sea innecesariamente grande ya
que ello nos puede conducir a un grave error de
redondeo.

22. Método M
•En este ejemplo, los coeficientes objetivo de X1 y X2
son 4 y 1, respectivamente, y parece razonable
establecer M=100.
•Utilizando M=100, la tabla simplex de inicio se da
como sigue (la columna z no cambia en todas las
iteraciones):

23. Método M
MinimizarZ Min = 4x1 + x2+ MR1 + MR2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 ≥ 0

24. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z
R1
R2
S2

25. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z -4 -1 0 -100 -100 0 0
R1
R2
S2

26. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z -4 -1 0 -100 -100 0 0
R1 3 1 0 1 0 0 3
R2
S2

27. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z -4 -1 0 -100 -100 0 0
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4

28. Método M
•Antes de proseguir con los cálculos del método
simplex, la fila Z debe hacerse consistente con el resto
de la tabla. El lado derecho de la fila Z en la tabla en
este momento muestra Z = 0. Sin embargo, dada la
solución no básica X1 = X2 = S1 = 0, la solución básica
actual (R1, R2, S2) = (3, 6, 4), la cual da Z = 100 X 3 +
100 X 6 + 4 X 0 = 900.

29. Método M
•Esta inconsistencia se deriva del hecho de que los
coeficientes de R1 y R2 no son cero (-100, -100) en la
fila Z (compare con la solución de inicio de total
holgura en los ejercicios anteriores, donde los
coeficientes en la fila z de las holguras son cero).

30. Método M
•Para eliminar la inconsistencia, tenemos que sustituir
R1 y R2 en la fila z por medio de la siguiente operación
de filas:
Nueva fila Z = Anterior fila Z + (100 x fila R1) +
(100 x fila R2)

31. Método M
x100 100 100 100 100 100 100 100
R1 3 1 0 1 0 0 3
Resultado
Z
Resultado

32. Método M
x100 100 100 100 100 100 100 100
R1 3 1 0 1 0 0 3
Resultado 300 100 0 100 0 0 300
Z
Resultado

33. Método M
x100 100 100 100 100 100 100 100
R1 3 1 0 1 0 0 3
Resultado 300 100 0 100 0 0 300
Z -4 -1 0 -100 -100 0 0
Resultado

34. Método M
x100 100 100 100 100 100 100 100
R1 3 1 0 1 0 0 3
Resultado 300 100 0 100 0 0 300
Z -4 -1 0 -100 -100 0 0
Resultado 296 99 0 0 -100 0 300

35. Método M
x100 100 100 100 100 100 100 100
R2 4 3 -1 0 1 0 6
Resultado 400 300 -100 0 100 0 600
Z 296 99 0 0 -100 0 300
Resultado 696 399 -100 0 0 0 900

36. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4

37. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Número más
positivo de “Z”
Dado que la función objetivo se
Minimiza, la variable X1 que tiene el
coeficiente más positivo

38. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4

39. Método M
Básica
Variables Solución Razón
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Razón

40. Método M
Básica
Variables Solución Razón
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3 3/3=1
R2 4 3 -1 0 1 0 6 6/4=3/2
S2 1 2 0 0 0 1 4 4/1=4

41. Método M
Básica
Variables Solución Razón
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3 3/3=1
R2 4 3 -1 0 1 0 6 6/4=3/2
S2 1 2 0 0 0 1 4 4/1=4
Seleccionamos el
Menor (positivo)

42. Método M
Básica
Variables Solución Razón
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3 3/3=1
R2 4 3 -1 0 1 0 6 6/4=3/2
S2 1 2 0 0 0 1 4 4/1=4

43. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 696 399 -100 0 0 0 900
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4

44. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 167 -100 -232 0 0 204
X1 1 1/3 0 1/3 0 0 1
R2 0 5/3 -1 -4/3 1 0 2
S2 0 5/3 0 -1/3 0 1 3

45. Método M
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 167 -100 -232 0 0 204
X1 1 1/3 0 1/3 0 0 1
R2 0 5/3 -1 -4/3 1 0 2
S2 0 5/3 0 -1/3 0 1 3

46. •Continuando con los cálculos
simplex, se requieren dos
iteraciones más para alcanzar el
óptimo.
Método M

47. Método M
Variable Valor
X1
= 2/5
X2
= 9/5
Z = 17/5

48. Método de dos fases
•En el método M, el uso de la penalización, M, puede
conducir a un error de redondeo.
•El método de dos fases elimina el uso de la constante
M. Como su nombre lo indica, el método resuelve la PL
en dos fases; en la fase I se trata de encontrar la
solución factible básica inicial y, si se halla una, se
invoca la fase II para resolver el problema original.

49. Fase I.
•Ponga el problema en forma de ecuación y agregue las
variables artificiales necesarias a las restricciones
(exactamente como en el método M), para tener la certeza
de una solución básica. A continuación, determine una
solución básica de la ecuación resultante que siempre
minimice la suma de las variables artificiales,
independientemente de si la PL es de maximización o
minimización. Si el valor mínimo de la suma es positivo, el
problema de PL no tiene una solución factible. De lo
contrario, si el valor mínimo es cero, prosiga con la fase II.

50. Fase II.
•Use la solución factible de la fase I como una solución
factible básica inicial para el problema original.

51. Minimizar Z Min = 4x1 + x2
Sujeto a: 3x1 + x2 = 3
4x1 + 3x2 ≥ 6
x1 + 2x2 ≤ 4
x1 , x2 ≥ 0
Método de dos fases

52. Minimizar Z Min = R1 + R2
Sujeto a: 3x1 + x2 + R1 = 3
4x1 + 3x2 - S1 + R2 = 6
x1 + 2x2 +S2 = 4
x1 , x2 , S1, S2 , R1. R2 ≥ 0
Fase I.

53. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z
R1
R2
S2
Método de dos fases

54. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 0 0 -1 -1 0 0
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Método de dos fases

55. Método de dos fases
•Como en el método M, R1 y R2 se sustituyen en la fila Z
mediante las siguientes operaciones de filas:
•Nueva fila Z = Anterior fila Z + (1 x fila R1) + (1 x fila R2)

56. x1 1 1 1 1 1 1 1
R1 3 1 0 1 0 0 3
Resultado
Z
Resultado
Método de dos fases

57. x1 1 1 1 1 1 1 1
R1 3 1 0 1 0 0 3
Resultado 3 1 0 1 0 0 3
Z
Resultado
Método de dos fases

58. x1 1 1 1 1 1 1 1
R1 3 1 0 1 0 0 3
Resultado 3 1 0 1 0 0 3
Z 0 0 0 -1 -1 0 0
Resultado
Método de dos fases

59. x1 1 1 1 1 1 1 1
R1 3 1 0 1 0 0 3
Resultado 3 1 0 1 0 0 3
Z 0 0 0 -1 -1 0 0
Resultado 3 1 0 0 -1 0 3
Método de dos fases

60. x1 1 1 1 1 1 1 1
R2 4 3 -1 0 1 0 6
Resultado
Z
Resultado
Método de dos fases

61. x1 1 1 1 1 1 1 1
R2 4 3 -1 0 1 0 6
Resultado 4 3 -1 0 1 0 6
Z
Resultado
Método de dos fases

62. x1 1 1 1 1 1 1 1
R2 4 3 -1 0 1 0 6
Resultado 4 3 -1 0 1 0 6
Z 3 1 0 0 -1 0 3
Resultado
Método de dos fases

63. x1 1 1 1 1 1 1 1
R2 4 3 -1 0 1 0 6
Resultado 4 3 -1 0 1 0 6
Z 3 1 0 0 -1 0 3
Resultado 7 4 -1 0 0 0 9
Método de dos fases

64. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 7 4 -1 0 0 0 9
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Método de dos fases

65. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 7 4 -1 0 0 0 9
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Método de dos fasesNúmero más
positivo de “Z”
Dado que la función objetivo se
Minimiza, la variable X1 que tiene el
coeficiente más positivo

66. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 7 4 -1 0 0 0 9
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Método de dos fases

67. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 7 4 -1 0 0 0 9
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
S2 1 2 0 0 0 1 4
Método de dos fases

68. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 5/3 -1 -7/3 0 0 2
X1 1 1/3 0 1/3 0 0 1
R2 0 5/3 -1 -4/3 1 0 2
S2 0 5/3 0 -1/3 0 1 3
Método de dos fases

69. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 5/3 -1 -7/3 0 0 2
X1 1 1/3 0 1/3 0 0 1
R2 0 5/3 -1 -4/3 1 0 2
S2 0 5/3 0 -1/3 0 1 3
Método de dos fases

70. Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
X2 0 1 -3/5 -4/5 3/5 0 6/5
S2 0 0 1 1 -1 1 1
Método de dos fases

71. Método de dos fases
•Como el mínimo Z = 0, la fase I produce la solución
factible básica
•En este punto, las variables artificiales ya completaron
su misión, y podemos eliminar sus columnas de la tabla
y continuar con la fase II.
Variable Valor
X1
= 3/5
X2
= 6/5

72. Fase II.
•Primero debemos eliminar las columnas artificiales.
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
X2 0 1 -3/5 -4/5 3/5 0 6/5
S2 0 0 1 1 -1 1 1

73. Fase II.
•Primero debemos eliminar las columnas artificiales.
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
X2 0 1 -3/5 -4/5 3/5 0 6/5
S2 0 0 1 1 -1 1 1

74. Fase II.
•Primero debemos eliminar las columnas artificiales.
Básica
Variables Solución
X1 X2 S1 R1 R2 S2
Z 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
X2 0 1 -3/5 -4/5 3/5 0 6/5
S2 0 0 1 1 -1 1 1

75. Fase II.
•Escribimos el problema original.
Básica
Variables Solución
X1 X2 S1 S2
Z 0 0 0 0 0
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2 0 0 1 1 1

76. Fase II.
•Escribimos el problema original.
Minimizar Z Min = 4x1 + x2
Sujeto a:

77. Fase II.
•Escribimos el problema original.
Minimizar Z Min = 4x1 + x2
Sujeto a: x1 + 1/5 S1 = 3/5

78. Fase II.
•Escribimos el problema original.
Minimizar Z Min = 4x1 + x2
Sujeto a: x1 + 1/5 S1 = 3/5
x2 - 3/5 S1 = 6/5

79. Fase II.
•Escribimos el problema original.
Minimizar Z Min = 4x1 + x2
Sujeto a: x1 + 1/5 S1 = 3/5
x2 - 3/5 S1 = 6/5
S1 + S2 = 1

80. Fase II.
•Escribimos el problema original.
Minimizar Z Min = 4x1 + x2
Sujeto a: x1 + 1/5 S1 = 3/5
x2 - 3/5 S1 = 6/5
S1 + S2 = 1
x1 , x2 , S1, S2 ≥ 0

81. Método de dos fases
•En esencia, la fase I ha transformado las ecuaciones de
restricciones originales de tal forma que proporciona
una solución factible básica inicial para el problema, si
es que existe una. La tabla asociada con la fase II del
problema es por consiguiente:

82. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z
X1
X2
S2

83. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z -4 -1 0 0 0
X1
X2
S2
Como en el simplex normal,
pasan negativos

84. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z -4 -1 0 0 0
X1 1 0 1/5 0 3/5
X2
S2

85. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z -4 -1 0 0 0
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2

86. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z -4 -1 0 0 0
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2 0 0 1 1 1

87. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z -4 -1 0 0 0
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2 0 0 1 1 1

88. Método de dos fases
•Una vez más, como las variables básicas X1 y X2 tienen
coeficientes diferentes a cero en la fila Z, deben ser
sustituidas, mediante las siguientes operaciones.
•Nueva fila Z = Anterior fila Z + (4 x fila X1) + (1 x fila X2)

89. x4 4 4 4 4 4
X1 1 0 1/5 0 3/5
Resultado
Z
Resultado
Método de dos fases

90. x4 4 4 4 4 4
X1 1 0 1/5 0 3/5
Resultado 4 0 4/5 0 12/5
Z
Resultado
Método de dos fases

91. x4 4 4 4 4 4
X1 1 0 1/5 0 3/5
Resultado 4 0 4/5 0 12/5
Z -4 -1 0 0 0
Resultado
Método de dos fases

92. x4 4 4 4 4 4
X1 1 0 1/5 0 3/5
Resultado 4 0 4/5 0 12/5
Z -4 -1 0 0 0
Resultado 0 -1 4/5 0 12/5
Método de dos fases

93. X1 1 1 1 1 1
X2 0 1 -3/5 0 6/5
Resultado
Z
Resultado
Método de dos fases

94. X1 1 1 1 1 1
X2 0 1 -3/5 0 6/5
Resultado 0 1 -3/5 0 6/5
Z
Resultado
Método de dos fases

95. X1 1 1 1 1 1
X2 0 1 -3/5 0 6/5
Resultado 0 1 -3/5 0 6/5
Z 0 -1 4/5 0 12/5
Resultado
Método de dos fases

96. X1 1 1 1 1 1
X2 0 1 -3/5 0 6/5
Resultado 0 1 -3/5 0 6/5
Z 0 -1 4/5 0 12/5
Resultado 0 0 1/5 0 18/5
Método de dos fases

97. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z 0 0 1/5 0 18/5
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2 0 0 1 1 1
•La tabla inicial de la fase II es por consiguiente

98. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z 0 0 1/5 0 18/5
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
S2 0 0 1 1 1
•La tabla inicial de la fase II es por consiguiente

99. Fase II.
Básica
Variables Solución
X1 X2 S1 S2
Z 0 0 0 -1/5 17/5
X1 1 0 0 -1/5 2/5
X2 0 1 0 3/5 9/5
S1 0 0 1 1 1

100. Variable Valor
X1
= 2/5
X2
= 9/5
Z = 17/5
Método de dos fases