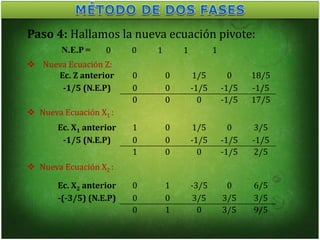
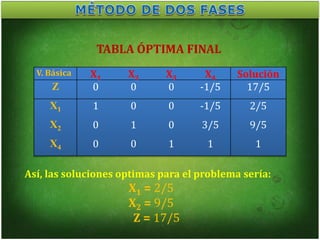
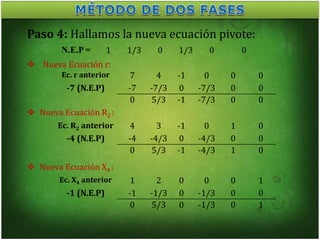
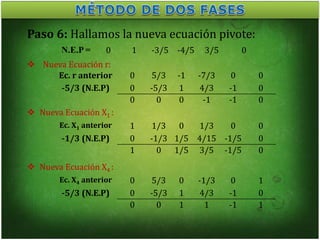
Este documento presenta la resolución de un problema de programación lineal mediante el método de las dos fases. En la primera fase se minimizan las variables holgura y exceso para obtener una solución factible al problema relajado. En la segunda fase se resuelve el problema original minimizando la función objetivo sujeta a las restricciones factibles.

1. “Año del Centenario de Machu Picchu para el Mundo”
CURSO: INVESTIGACIÓN DE OPERACIONES I
JOSÉ FAUSTINO SÁNCHEZ CARRIÓN
Facultad de Ingeniería - EAP INGENIERÍA INDUSTRIAL
ALUMNAS: BELLON PACHECO, GERALDINE MARLENI
RAMIREZ MONTALVO , AYDA MARIBEL

2. Minimizar: Z = 4 X1 + X2
s.a:
3 X1 + X2 = 3
4 X1 + 3X2 ≥ 6
X1 + 2X2 ≤ 4
X1, X2 ≥ 0
 EJEMPLO DE APLICACIÓN:

3. Min Z = 4 X1 + X2 + MR1 + MR2
s.a:
3 X1 + X2 + R1 + = 3
4 X1 + 3X2 - X3 + R2 + = 6
X1 + 2X2 + X4 = 4
SOLUCIÓN: Añadimos las variables de holgura
y exceso para aplicar el método de dos fases:

4. FASE I:
Minimizar r = R1 + R2
s.a:
3 X1 + X2 + R1 + = 3
4 X1 + 3X2 - X3 + R2 + = 6
X1 + 2X2 + X4 = 4
X1, X2, X3, X4, R1, R2 ≥ 0
Paso 1: Minimizar r:

5. V. Básica X1 X2 X3 R1 R2 X4 Solución
r 0 0 0 -1 -1 0 0
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
X4 1 2 0 0 0 1 4
V. Básica X1 X2 X3 R1 R2 X4 Solución
r 7 4 -1 0 0 0 9
R1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
X4 1 2 0 0 0 1 4
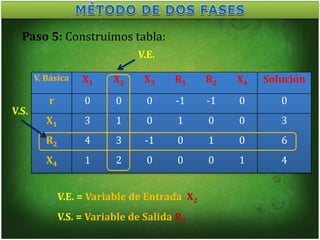
Paso 2: Construimos tabla:
Nuevo renglón r = Renglón r anterior + [1 x Renglón R1 + 1 x Renglón R2]
Paso 3: Construimos nueva tabla:
-

6. Paso 4: Hallamos la nueva ecuación pivote:
N.E.P = 1 1/3 0 1/3 0 0
Ec. r anterior 7 4 -1 0 0 0
-7 (N.E.P) -7 -7/3 0 -7/3 0 0
0 5/3 -1 -7/3 0 0
 Nueva Ecuación r:
 Nueva Ecuación R2 :
Ec. R2 anterior 4 3 -1 0 1 0
-4 (N.E.P) -4 -4/3 0 -4/3 0 0
0 5/3 -1 -4/3 1 0
 Nueva Ecuación X4 :
Ec. X4 anterior 1 2 0 0 0 1
-1 (N.E.P) -1 -1/3 0 -1/3 0 0
0 5/3 0 -1/3 0 1

7. V. Básica X1 X2 X3 R1 R2 X4 Solución
r 0 0 0 -1 -1 0 0
X1 3 1 0 1 0 0 3
R2 4 3 -1 0 1 0 6
X4 1 2 0 0 0 1 4
Paso 5: Construimos tabla:
V.E.
-
V.S.
V.E. = Variable de Entrada X2
V.S. = Variable de Salida R2

8. Paso 6: Hallamos la nueva ecuación pivote:
N.E.P = 0 1 -3/5 -4/5 3/5 0
Ec. r anterior 0 5/3 -1 -7/3 0 0
-5/3 (N.E.P) 0 -5/3 1 4/3 -1 0
0 0 0 -1 -1 0
 Nueva Ecuación r:
 Nueva Ecuación X1 :
Ec. X1 anterior 1 1/3 0 1/3 0 0
-1/3 (N.E.P) 0 -1/3 1/5 4/15 -1/5 0
1 0 1/5 3/5 -1/5 0
 Nueva Ecuación X4 :
Ec. X4 anterior 0 5/3 0 -1/3 0 1
-5/3 (N.E.P) 0 -5/3 1 4/3 -1 0
0 0 1 1 -1 1

9. V. Básica X1 X2 X3 R1 R2 X4 Solución
r 0 0 0 -1 -1 0 0
X1 1 0 1/5 3/5 -1/5 0 3/5
R2 0 1 -3/5 -4/5 3/5 0 6/5
X4 0 0 1 1 -1 1 1
TABLA ÓPTIMA

10. FASE II:
Minimizar = 4 X1 + X2
s.a:
X1 + 0X2 – X3 + X4 = 3/5
0X1 + X2 – X3 + X4 = 6/5
X3 + X4 = 1
X1, X2, X3, X4, ≥ 0
Paso 1: Después de eliminar las columnas
artificiales, se reescribe el problema original:

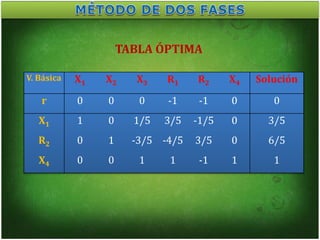
11. V. Básica X1 X2 X3 X4 Solución
r 0 0 1/5 0 18/5
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
X4 0 0 1 1 1
Paso 2: Construimos tabla:
Nuevo renglón Z = Renglón Z anterior + [4 x Renglón X1 + 1 x Renglón X2]
V. Básica X1 X2 X3 X4 Solución
r 0 0 1/5 0 18/5
X1 1 0 1/5 0 3/5
X2 0 1 -3/5 0 6/5
X4 0 0 1 1 1
Paso 3: Reemplazando:
-

12. Paso 4: Hallamos la nueva ecuación pivote:
N.E.P = 0 0 1 1 1
Ec. Z anterior 0 0 1/5 0 18/5
-1/5 (N.E.P) 0 0 -1/5 -1/5 -1/5
0 0 0 -1/5 17/5
 Nueva Ecuación Z:
 Nueva Ecuación X1 :
 Nueva Ecuación X2 :
Ec. X1 anterior 1 0 1/5 0 3/5
-1/5 (N.E.P) 0 0 -1/5 -1/5 -1/5
1 0 0 -1/5 2/5
Ec. X2 anterior 0 1 -3/5 0 6/5
-(-3/5) (N.E.P) 0 0 3/5 3/5 3/5
0 1 0 3/5 9/5

13. V. Básica X1 X2 X3 X4 Solución
Z 0 0 0 -1/5 17/5
X1 1 0 0 -1/5 2/5
X2 0 1 0 3/5 9/5
X4 0 0 1 1 1
TABLA ÓPTIMA FINAL
Así, las soluciones optimas para el problema sería:
X1 = 2/5
X2 = 9/5
Z = 17/5