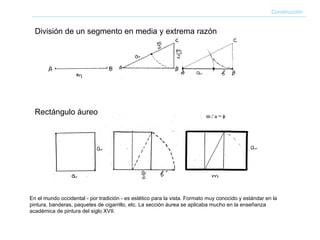
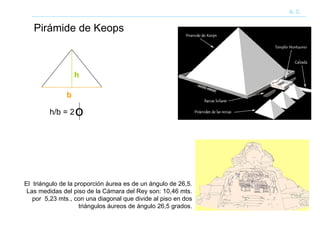
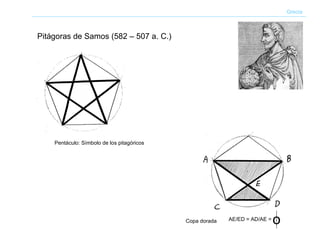
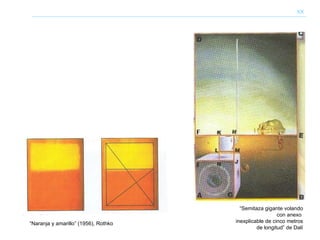
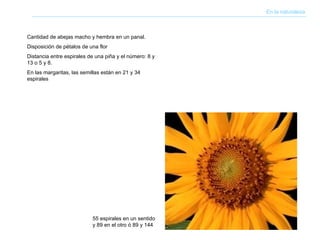
El documento describe brevemente la historia y aplicaciones del número áureo o sección áurea. Ha sido utilizado en la arquitectura de edificios antiguos como las Puertas de Ishtar y la Pirámide de Keops. También se aplicó en el arte del Renacimiento y en obras de arquitectos como Le Corbusier. El número áureo aparece con frecuencia en la naturaleza en la disposición de espirales, flores y conchas. También se ha relacionado con proporciones musicales.

1. EL Nº DE ORO Y LA SECCIÓN ÁUREA Presentación creada para el edublog http://espiralcromatica.wordpress.com

2. Nº de oro, razón áurea o nº de Fidias * Construcción. División de un segmento en media y extrema razón. Rectángulo áureo * a. C. Puertas de Ishtar Pirámide de Keops * GRECIA -Euclides Pitágoras * XIII: FIBONACCI * XV * Renacimiento: Boticelli y Brunelleschi * XVIII * XX: Mondrian, Puntos de oro, Le corbusier, Dalí, Rothko * Naturaleza * Música

3. Construcción División de un segmento en media y extrema razón En el mundo occidental - por tradición - es estético para la vista. Formato muy conocido y estándar en la pintura, banderas, paquetes de cigarrillo, etc. La sección áurea se aplicaba mucho en la enseñanza académica de pintura del siglo XVII. Rectángulo áureo

4. El menor es al mayor como el mayor es al total Construcción ¿De dónde sale phi? x 1 1 / x = x / x + 1 x + 1 = x x – x + 1 = 0 x = 1 + V 1 + 4 / 2 2 2

5. Puertas de Ishtar A. C. Están en el museo de Pérgamo (Berlín, 1930). Era una de las 8 puertas monumentales (14x10) de la muralla interior de Babilonia, por la que se accedía al templo de Bel donde se celebraban las fiestas del año nuevo.

6. Pirámide de Keops A. C. El triángulo de la proporción áurea es de un ángulo de 26,5. Las medidas del piso de la Cámara del Rey son: 10,46 mts. por 5,23 mts., con una diagonal que divide al piso en dos triángulos áureos de ángulo 26,5 grados. h/b = 2 o b h

7. Partenon Grecia Iniciado por Pericles y se desarrolló entre los años 447 y 432 a. C. Los arquitectos encargados de la obra fueron Ictino y Calícrates y estuvieron, en la mayoría de los casos, bajo las órdenes del famoso escultor ateniense Fidias.

8. Grecia éntasis Las cosas no son lo que parecen…

9. Pitágoras de Samos (582 – 507 a. C.) Copa dorada Pentáculo: Símbolo de los pitagóricos Grecia AE/ED = AD/AE = o

10. D-L/L = L/D R-L/L = L/R Grecia El lado del decágono es áureo del radio El lado del pentágono es áureo de su diagonal Propiedades del pentágono y del decágono

11. Fibonacci (Leonardo da Pisa) (1170-1250) filius Bonacci XIII Gráfica de la secuencia de Fibonacci extendida al campo de los números reales Cada término es la suma de los dos anteriores "Una pareja de conejos tarda un mes en alcanzar la edad fértil, a partir de ese momento cada vez engendra una pareja de conejos, que a su vez, tras ser fértiles engendrarán cada mes una pareja de conejos. ¿Cuántos conejos habrá al cabo de un determinado número de meses?." Parejas: 1 primer mes 2 segundo mes 3 tercer mes 5 cuarto mes 8 quinto mes 13 sexto mes 21 séptimo mes 34 octavo mes 55 noveno mes 89 décimo mes 144 undécimo mes 233 duodécimo mes 377

12. XIII Rectángulo basado en la serie de Fibonacci Si unimos los vértices de estos rectángulos se nos va formando una curva que ya nos resulta familiar. Es la espiral de Durero

13. Luca Pacioli y Leonardo da Vinci Isabella d´Este Hombre de Vitrubio (ilustración para La divina proporción , 1509) Renacimiento RELACIÓN: Altura total y ombligo Distancia hombros – dedos y codo – dedos Altura de la cadera y altura de la rodilla Divisiones vertebrales Aritculaciones manos y pies = lado de cuadrado/ radio de circunferencia o

14. Boticelli Renacimiento “ Nacimiento de Venus ” de Boticelli

15. “ Santa Mª Novella” con cúpula de Brunelleschi, fachada de León Battista Alberti Renacimiento

16. Retratos en el Renacimiento “ Enrique VIII” de Hans Holbein “El joven” “ Giovanna Tornabuoni” de Ghirlandaio Renacimiento

17. Goya “ Los fusilamientos del 2 de Mayo” XVIII

18. Siglo XX Puntos de oro “ El circo” de Seurat “ Composición I” de Piet Mondrian XX

19. Le Corbusier XX Ideó el Modulo r, sistema de medidas en que cada magnitud se relaciona con la anterior por el Número Áureo , para que sirviese de medida de las partes de arquitectura. Tomó como escala el francés medio de 1,70 m de estatura; más adelante añadió el policía británico de 6 pies (1,83 m), lo que dio el Modulor II.

20. “ Unidad de habitación” (Berlín) XX “ Unidad de habitación” (Marsella)

21. XX “ Semitaza gigante volando con anexo inexplicable de cinco metros de longitud” de Dalí “ Naranja y amarillo” (1956), Rothko

22. En la naturaleza 55 espirales en un sentido y 89 en el otro ó 89 y 144 Cantidad de abejas macho y hembra en un panal. Disposición de pétalos de una flor Distancia entre espirales de una piña y el número: 8 y 13 o 5 y 8. En las margaritas, las semillas están en 21 y 34 espirales

23. solarium perspectivum triton tritonis nautilius pompilius cardium pseudolima En la naturaleza

24. En la estructura formal de: Tema de la 5ª sinfonía de Beethoven ( Llamada del Destino ) Proporción entre el desarrollo del tema e introducción en sonatas de Mozart En obras de Shubert y Debussy Bela Bártok y Olivier Messiaen y Stockhausen lo utilizan para determinar la duración de notas y las unidades formales se relacionan (a propósito) con el número áureo Música La ubicación de las efes (los “oídos”, u orificios en la tapa) se relaciona con el número áureo.