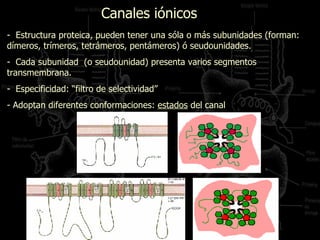
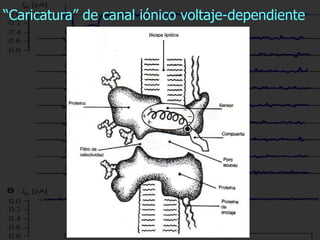
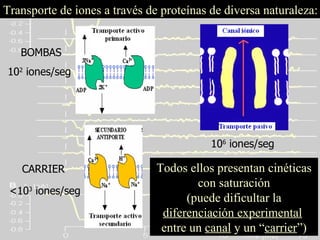
El documento describe los diferentes mecanismos de transporte iónico a través de la membrana celular, incluyendo la electrodifusión libre a través de canales iónicos. Explica que la electrodifusión ocurre de forma pasiva siguiendo el gradiente electroquímico, y que los canales iónicos confieren alta especificidad al transporte de iones como Na+, K+, Ca++ y Cl-. También presenta las ecuaciones que rigen este proceso, como la ley de Nernst y la ecuación de Goldman-Hodgkin-Katz para

1. Electrodifusión libre Canales iónicos

2. Electrodifusión libre Transporte pasivo (a favor de gradiente electroquímico Especie transportada: pequeños iones inorgánicos (Na + , K + , Ca ++ , Cl - ) A través de canales iónicos (gran mayoría: alta especificidad) Participan en múltiples funciones : Excitabilidad Proliferación celular Comunicación intercelular Fecundación Acoplamientos excito-contractor y excito-secretor Mantenimiento y regulación del volumen celular Transducción sensorial Aprendizaje y memoria Procesos de absorción y excreción Balance hidroelectrolítico Secreción de hormonas

3. Energía de un soluto en solución tiene dos componentes: químico y eléctrico: Energía potencial química: Epq = RTlnC Energía potencial eléctrica: Epe = zFV Energía potencial total: Ept = Epq + Epe Condición de equilibrio para un soluto (en célula): Ept i = Ept e Epq i + Epe i = Epq e + Epe e Leyes que rigen la Electrodifusión libre

4. V i -V e = RT/zF. ln (C e /C i ) = Ex Por propiedad logarítmica: LEY DE NERNST (Ex: Potencial de equilibrio del ion X) Epq i + Epe i = Epq e + Epe e Sustituyo por sus componentes: RTlnC i + zFV i = RTlnC e + zFV e Reordenando: zFV i - zFV e = RTlnC e - RTlnC i Sacando factor común: zF (V i -V e ) = RT (lnC e – lnC i ) Reordenando: V i -V e = RT/zF. (lnC e – lnC i )

5. Epq i + Epe i = Epq e + Epe e Sustituyendo por sus componentes: RTlnC i + zFV i = RTlnC e + zFV e Operando y reordenando: V i -V e = RT/zF. ln (C e /C i ) = E x LEY DE NERNST (Condición de equilibrio para un ion)

6. Dado que cada ion tiene sus propias condiciones de concentración y carga: (Datos para iones más relevantes en fibra muscular esquelética) (Utilizando: R = 8,3 J/mol.K; t = 25°C y F = 96500 C/mol) E Na+ = +64 mV E K+ = -94mV E Cl- = -89 mV Concentración extracelular Concentración intracelular Na + 145 mM 12 mM K + 4 mM 155 mM Cl - 120 mM 3,8 mM

7. Condición de equilibrio para un ion: Vm = E, ¿En qué situación el ión poseerá cierta energía potencial electroquímica que le dé “tendencia al escape”? I X z = g X z . (Vm – E X z ) LEY de OHM para canales iónicos I Na + = g Na + . (V m – E Na + ) I K + = g K + . (V m – E K + ) Ó ¿Cuál será la fuerza impulsora para un ión? I Cl - = g Cl - . (V m – E Cl - ) V m – E X z

8. ¿Cómo modifica al Vm, una corriente iónica transportada por...? un catión (+) que ingresa a la célula? que egresa de la célula? un anión (-) que ingresa a la célula? que egresa de la célula? En la gran mayoría de células, cuando la membrana está en reposo : - El Na + tiende a ingresar y depolarizar la membrana - El K + tiende a egresar e hipoerpolarizar la membrana - El Cl - está en equilibrio (no tiene tendencia al escape)

9. Vm 0 E Na E K Vr I entrante de Na+ I saliente de K+

10. Vm 0 E Na E K Vr (2) La técnica de fijación de voltaje permite modificar el Vm y eventualmente invertir las corrientes iónicas Vr (1) I saliente de Na+ I entrante de K+ Vr anterior

11. ¿De qué otra forma se podría experimentalmente invertir una corriente iónica? ¿En qué condiciones la corriente iónica será nula? Recordemos las ecuaciones de flujo pasivo que estudiamos y la ley general del transporte: I X z = g X z . (Vm – E X z ) Ley de Ohm para canales iónicos J/á = - L. dY/dx Ley general del transporte M = P. dC Primera ley de Fick  J = L. (  P  )  Ecuación de flujo de agua

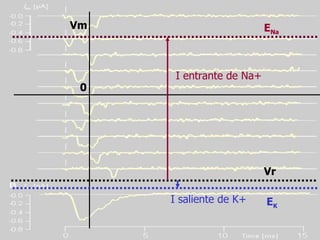
12. Ecuación de Goldmann-Hodking y Katz Retomamos ley de Ohm para canales iónicos: I X z = g X z . (Vm – E X z ) El voltaje de membrana es afectado por la conductancia (“permeabilidad”) a los diferentes iones y sus correspondientes potenciales de equilibrio V reposo = R.T zF ln P Na + . [Na] e + P K + . [K] e + P Cl - . [Cl - ] i P Na + . [Na] i + P K + . [K] i + P Cl - . [Cl - ] e

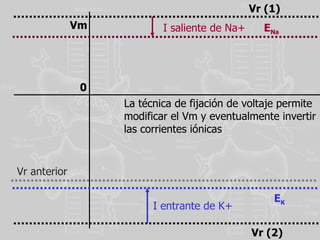
13. El voltaje de membrana de reposo se acerca al potencial de equilibrio del ión más permeante “ Caso extremo”: la membrana es permisiva a un solo ion Ej: al Na+: V reposo = R.T zF ln P Na + . [Na] e + P K + . [K] e + P Cl - . [Cl - ] i P Na + . [Na] i + P K + . [K] i + P Cl - . [Cl - ] e V reposo = R.T zF ln P Na + . [Na] e P Na + . [Na] i = E Na

14. La bomba de sodio y potasio sólo es relevante en la determinación del potencial de membrana de reposo indirectamente , manteniendo los gradientes electroquímicos de sodio y potasio En la mayoría de las células la ecuación de GHK es apropiada para calcular el Vm de reposo . (Hay excepciones, ej: células del órgano de Corti). El principal determinente del potencial de membrana de reposo es una alta permeabilidad al potasio, respecto al sodio: P K > P Na (cambios en K+e importantes efectos en Vm y actividad eléctrica de células excitables) También participa la diferente distribución iónica a ambos lados de la membrana celular

15. - Estructura proteica, pueden tener una sóla o más subunidades (forman: dímeros, trímeros, tetrámeros, pentámeros) ó seudounidades. Cada subunidad (o seudounidad) presenta varios segmentos transmembrana. Especificidad: “filtro de selectividad” Adoptan diferentes conformaciones: estados del canal Canales iónicos

16. Clasificación de canales : - voltaje-dependientes - ligando-dependientes (ionotrópicos y metabotrópicos) - mecanosensibles Algunas variantes estructurales dependiendo del tipo de canal : - Presencia de segmento S4 (sensor de voltaje): grupo aminoacídico cargado que se mueve dependiendo del voltaje de membrana. - Presencia de zonas de unión a ligandos. - Mecanosensibles: mecanismo no bien comprendido

17. Canales ligando-dependientes Ejemplo: canales dependientes de receptores de acetilcolina (permiten el paso de sodio y potasio) Nicotínicos: el receptor está en el propio canal (ionotrópico) Muscarínicos: el receptor está en otra molécula proteica distinta del canal (metabotrópico) Dentro de metabotrópicos hay: - dependientes de proteína G y - dependientes de tirosinquinasa

18. “ Caricatura” de canal iónico voltaje-dependiente

19. Proteínas “transportadoras” Acuaporinas (t. pasivo) (cinética lineal) Canales iónicos (t. pasivo) (cinética con saturación) Bombas (t. activo primario) (saturación) “ Carriers” o “proteínas transportadoras” propiamente dichas (diversos tipos): “ simple”: transporta un único soluto (t.pasivo) (saturación) ; o “ transportes acoplados”: simporte (cotransporte) o antiporte (contratransporte) (t. activo secundario) (saturación)

20. Transporte de iones a través de proteínas de diversa naturaleza: 10 2 iones/seg BOMBAS CARRIER < 10 3 iones/seg 10 6 iones/seg Todos ellos presentan cinéticas con saturación (puede dificultar la diferenciación experimental entre un canal y un “ carrier ”)

21. Parámetros: - J máx : flujo máximo - Km : relación inversa con la afinidad “aparente” del transportador por el soluto Función doble inversa permite estimación más precisa de parámetros. [ ] [ ] J J max 1 / J [soluto] 1 / [soluto] J max J max