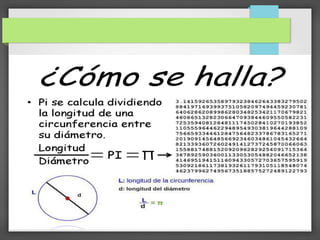
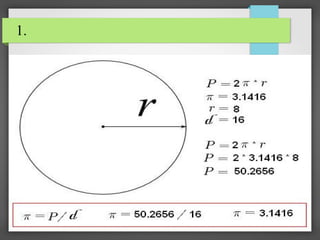
Este documento trata sobre el número pi. Explica que pi representa la relación entre la circunferencia y el diámetro de un círculo y que es un número irracional e importante en matemáticas, física e ingeniería. Detalla la historia del cálculo de pi por los antiguos egipcios, babilonios y griegos como Arquímedes, y cómo matemáticos posteriores como Fibonacci y van Roomen mejoraron las aproximaciones de pi. Finalmente, discute el uso del símbolo pi y cómo se popularizó su notación actual

1. INSTITUTO NACIONAL DE SAN RAFAEL
MAESTRO: JOSÉ RIGOBERTO GUARDADO.
ALUMNA: TATIANAABIGAIL REINA.
MATERIA: MATEMÁTICA
TEMA: EL NUMERO Pi.
GRADO: PRIMER AÑO DE BACHILLERATO GENERAL.
SECCIÓN: B.
AÑO: 2019.

2. OBJETIVOS
➢ANALIZAR LA IMPORTANCIA DEL NUMERO PI.
➢IDENTIFICAR QUE MEDIANTE EL SE PUEDE CALCULAR EL
PERÍMETRO DE U CIRCULO Y QUE ES LA PROPORCIÓN MAS EXACTA
AL ESTUDIAR LOS CÍRCULOS.

3. Historia del cálculo de pi
Los antiguos egipcios (hacia 1600 a. de C.) ya sabían que existía una
relación entre la longitud de la circunferencia y su diámetro; y entre el
área del círculo y el diámetro al cuadrado (seguramente de forma
intuitiva). En el Papiro de Rhind puede leerse lo siguiente: "Corta 1/9
del diámetro y construye un cuadrado sobre la longitud restante. Este
cuadrado tiene el mismo área que el circulo". Es decir, el área del
círculo (llamémosla A) es igual a 8/9 del diámetro al cuadrado (d=2r),
A = d2*64/81 = 4r2*64/81 = r2*256/81. Esto equivale a decir que
asignaban a π el valor 256/81, aproximadamente 3'16.
En Mesopotamia, más o menos por la misma época, los babilonios
utilizaban el valor 3'125 (3+1/8) según puede leerse en la Tablilla de
Susa.

4. Los geómetras de la Grecia clásica sabían que la razón entre la
longitud de una circunferencia cualquiera y su diámetro es
siempre una constante (el número al que ahora llamamos pi).
También conocían y habían conseguido demostrar que tanto la
razón entre el área de un círculo y su diámetro al cuadrado,
como la del volumen de una esfera y el cubo de su diámetro
eran constantes (desconocidas en aquel momento, libro XII de
"Los Elementos" de Euclides). Fue Arquímedes (siglo III a. de C.)
quien determinó que estas constantes estaban estrechamente
relacionadas con π. Además, utilizó el método de exhaución,
inscribiendo y circunscribiendo en una circunferencia polígonos
de hasta 96 lados y consiguiendo una magnífica aproximación
(si tenemos en cuenta los medios con los que contaba),
3+10/71 < π < 3+1/7; es decir, el número buscado está entre
3'1407 y 3'1428 (se puede ver en su obra "Sobre la medida del
circulo").

5. π (pi) es la relación entre la longitud de una circunferencia y su diámetro
en geometría euclidiana.1​ Es un número irracional2​ y una de las
constantes matemáticas más importantes. Se emplea frecuentemente en
matemáticas, física e ingeniería.
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la
historia, siendo una de las constantes matemáticas que más aparece en las
ecuaciones de la física, junto con el número e. Cabe destacar que el
cociente entre la longitud de cualquier circunferencia y la de su diámetro
no es constante en geometrías no euclidianas.
.

7. La notación con la letra griega π proviene de la inicial de las palabras de
origen griego περιφέρεια 'periferia' y περίμετρον 'perímetro' de un
círculo,5​ notación que fue utilizada primero por William Oughtred (1574-
1660) y cuyo uso fue propuesto por el matemático galés William Jones6​
(1675-1749); aunque fue el matemático Leonhard Euler, con su obra
Introducción al cálculo infinitesimal, de 1748, quien la popularizó. Fue
conocida anteriormente como constante de Ludolph (en honor al
matemático Ludolph van Ceulen) o como constante de Arquímedes (que
no se debe confundir con el número de Arquímedes). Jones plantea el
nombre y símbolo de este número en 1706 y Euler empieza a difundirlo
en 1736.7​

8. A partir del siglo XII, con el uso de cifras arábigas en los cálculos, se facilitó
mucho la posibilidad de obtener mejores cálculos para π. El matemático
Fibonacci (1170-1250), en su Practica Geometriae, amplifica el método de
Arquímedes, proporcionando un intervalo más estrecho. Algunos matemáticos
del siglo XVII, como Viète, usaron polígonos de hasta 393 216 lados para
aproximarse con buena precisión a 3.141592653. En 1593 el flamenco Adriaan
van Roomen (Adrianus Romanus) obtiene una precisión de 16 dígitos decimales
usando el método de Arquímedes.

9. El inglés William Oughtred fue el primero que empleó la letra griega π como
símbolo del cociente entre las longitudes de una circunferencia y su diámetro.
Fue en el año 1706 cuando el galés William Jones afirmó: «3.14159 andc. = π» y
propuso usar siempre el símbolo π, y fue Leonhard Euler el que al adoptarlo en
1737 lo convirtió en la notación habitual que se usa hasta nuestros días.
El matemático japonés Takebe empezó a calcular el número π en el año 1722,
con el mismo método expuesto por Arquímedes, y fue ampliando el número de
lados para polígonos circunscritos e inscritos hasta llegar a 1024 lados. Este
ingente trabajo consiguió que se determinara π con 41 decimales.

11. EJERCICIOS

12. 1.

13. 2.

15. CONCLUSIÓN
Pi no es sólo el sonido que hace la tele cuando alguien en la
tele dice una palabrota, ni es el sonido que hace el claxon de
un coche; Pi es una letra griega que representa un número
que es el 3,1415 y la relación entre el número Pi y la
circunferencia es el círculo.