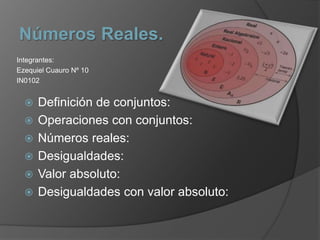
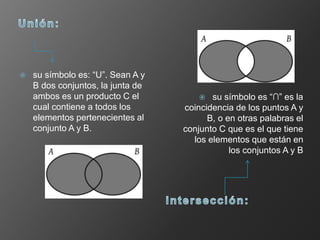
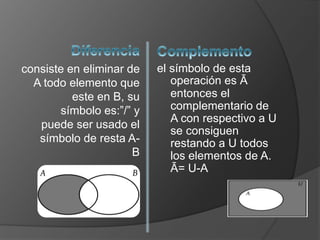
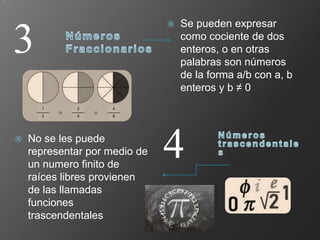
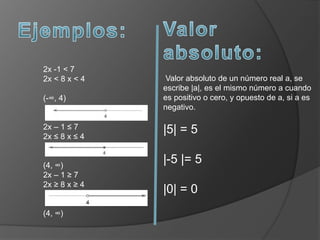
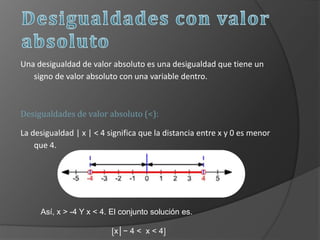
Este documento define los números reales y conceptos relacionados como conjuntos, operaciones con conjuntos, desigualdades y valor absoluto. Los números reales incluyen números racionales con expansión decimal periódica e irracionales con expansión no periódica. Se explican las propiedades de las desigualdades y cómo resolver desigualdades de valor absoluto considerando si la expresión dentro es positiva o negativa.

1. Números Reales.
Integrantes:
Ezequiel Cuauro Nº 10
IN0102
 Definición de conjuntos:
 Operaciones con conjuntos:
 Números reales:
 Desigualdades:
 Valor absoluto:
 Desigualdades con valor absoluto:

2. El conjunto de los números reales contiene a todos los
números que tienen lugar en la recta numérica.
Podemos definirlo como la combinación de dos tipos
de números, los racionales (o que poseen una
expansión decimal periódica) y los irracionales (que
poseen una expansión racional no periódica).
Ejemplo:
 0,3333333… es real ya que 0,3333333= 1/3
 3 es real ya que 3=3,00000
 ½ es real ya que ½=0.5
 1243,200200200200200200…. Es real ya que tiene
una secuencia decimal infinita.

3. Nos permite
realizar
operaciones
sobre los
conjuntos
para Obtener
otro conjunto.
Este método
posee distintas
operaciones:

4.  su símbolo es: “U”. Sean A y
B dos conjuntos, la junta de
ambos es un producto C el
cual contiene a todos los
elementos pertenecientes al
conjunto A y B.
 su símbolo es “∩” es la
coincidencia de los puntos A y
B, o en otras palabras el
conjunto C que es el que tiene
los elementos que están en
los conjuntos A y B

5. consiste en eliminar de
A todo elemento que
este en B, su
símbolo es:”/” y
puede ser usado el
símbolo de resta A-
B
el símbolo de esta
operación es Ᾱ
entonces el
complementario de
A con respectivo a U
se consiguen
restando a U todos
los elementos de A.
Ᾱ= U-A

6. Su símbolo es ∆ la diferencial
simétrica de dos conjuntos A y B es otro
conjunto el cual posee los elementos que o
bien se encuentran A, o bien se encuentran
en B pero no en ambos lados a la vez. A ∆
B =C, donde C no tiene

7. Son aquellos que tienen expansión
decimal periódica o tienen expansión
decimal no periódica. Pueden ser
representados en la recta numérica entre
ellos están los:
 Números enteros
 Números naturales
 Números Fraccionarios
 Números trascendentales

8. (N), los usamos para contar
(1, 2, 3, 4, 5, 6, 7, 8,
9….)
(Z), son los números
naturales, sus negativos
y el cero (-3, -2, -1, 0, 1,
2, 3,)….
1
2

9.  Se pueden expresar
como cociente de dos
enteros, o en otras
palabras son números
de la forma a/b con a, b
enteros y b ≠ 0
 No se les puede
representar por medio de
un numero finito de
raíces libres provienen
de las llamadas
funciones
trascendentales
3
4

10. Es una relación de orden que se da entre
dos valores en cuestión que son
elementos de un conjunto ordenado y,
son relacionados por uno de estos
signos:
 Menor que: <
 Mayor que: >
 Menor o igual que: ≤
 Mayor o igual que: ≥
Su solución es el conjunto
de valores de la variable
que la verifica. Y se
representa por medio de:
 Una representación
grafica.
Un intervalo.
≤
< >
≥

11. 2x -1 < 7
2x < 8 x < 4
(-∞, 4)
2x – 1 ≤ 7
2x ≤ 8 x ≤ 4
(4, ∞)
2x – 1 ≥ 7
2x ≥ 8 x ≥ 4
(4, ∞)
Valor absoluto de un número real a, se
escribe |a|, es el mismo número a cuando
es positivo o cero, y opuesto de a, si a es
negativo.
|5| = 5
|-5 |= 5
|0| = 0

12.  Los números opuestos tienen igual valor absoluto.
A = -A
5 = -5
 El valor absoluto de un producto es igual al producto de
valores absolutos de los factores.
 El valor absoluto de una suma es menor o igual que la
suma de los valores absolutos de los sumandos.

13. Una desigualdad de valor absoluto es una desigualdad que tiene un
signo de valor absoluto con una variable dentro.
Desigualdades de valor absoluto (<):
La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor
que 4.
Así, x > -4 Y x < 4. El conjunto solución es.
⦋x│− 4 < x < 4⦌

14. 1. La expresión dentro de los símbolos de valor
absoluto es positiva.
2. La expresión dentro de los símbolos de valor
absoluto es negativa.
La solución es la intersección de las soluciones de
estos dos casos. En otras palabras, para
cualesquiera números reales a y b, si | a | < b,
entonces a < b Y a > - b.

15. Desigualdades de valor absoluto (>):
La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que
4.
Así, x < -4 O x > 4. El conjunto solución es:
⦋x│x < − 4 O x > 4⦌
Cuando se resuelven desigualdades de valor absoluto, hay dos casos a
considerar.
La expresión dentro de los símbolos de valor absoluto es positiva.
La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera números reales a y b , si | a | > b ,
entonces a > b O a < - b .