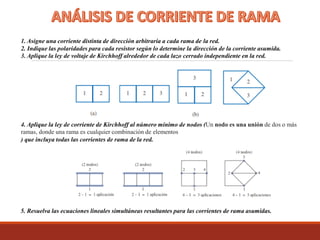
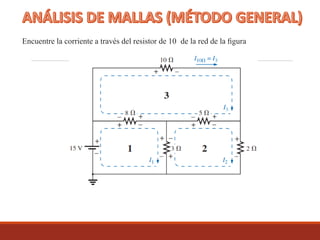
El documento describe el procedimiento para analizar una red eléctrica utilizando las leyes de Kirchhoff y el método de corriente de rama. Se detalla el proceso de asignar direcciones a las corrientes, determinar las polaridades de los resistores, y aplicar las leyes de voltaje y corriente de Kirchhoff en nodos y lazos de la red. Se presenta un enfoque para resolver ecuaciones lineales simultáneas derivadas del análisis de la red para encontrar las corrientes y voltajes en los nodos.

1. República Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación Universitaria
Universidad Territorial Politécnica José Antonio Anzoátegui

2. 1. Asigne una corriente distinta de dirección arbitraria a cada rama de la red.
2. Indique las polaridades para cada resistor según lo determine la dirección de la corriente asumida.
3. Aplique la ley de voltaje de Kirchhoff alrededor de cada lazo cerrado independiente en la red.
4. Aplique la ley de corriente de Kirchhoff al número mínimo de nodos (Un nodo es una unión de dos o más
ramas, donde una rama es cualquier combinación de elementos
) que incluya todas las corrientes de rama de la red.
5. Resuelva las ecuaciones lineales simultáneas resultantes para las corrientes de rama asumidas.

3. Aplique el método de corriente de rama a la red de la figura
Paso 3: Se aplica la ley de voltaje de Kirchhoff alrededor de cada lazo cerrado (1 y 2) en el
sentido de las manecillas del reloj:

4. Paso 4: Al aplicar la ley de corriente de Kirchhoff al nodo a (en una red de dos nodos, la
ley se aplica sólo sobre un nodo),
Paso 5: Existen tres ecuaciones y tres incógnitas (se eliminan las unidades para mayor
claridad):

5. En lugar de utilizar determinantes de tercer orden como en la solución anterior, es
posible reducir las tres ecuaciones a dos mediante la sustitución de la tercera ecuación en
las ecuaciones primera y segunda:

6. Encuentre la corriente a través del resistor de 10 de la red de la figura

8. 1. Determine el número de nodos dentro de la red.
2. Escoja un nodo de referencia, y etiquete cada nodo restante con un valor de voltaje con subíndice: V1, V2,
etcétera.
3. Aplique la ley de corriente de Kirchhoff sobre cada nodo excepto sobre el de referencia. Asuma que todas
las corrientes desconocidas abandonan el nodo por cada aplicación de la ley de corriente de Kirchhoff. En
otras palabras, para que cada nodo no se vea influenciado por la dirección que una corriente desconocida en
otro nodo pudiera haber tenido. Cada nodo se debe tratar como una entidad distinta e independiente de la
aplicación de la ley de corriente de Kirchhoff a los otros nodos.
4. Resuelva las ecuaciones resultantes para los voltajes nodales.
Aplique el análisis de nodos a la red de la figura

9. Pasos 1 y 2: La red cuenta con dos nodos, como se muestra en la figura. El nodo
inferior se define como el nodo de referencia al potencial de tierra (cero volts), y el otro
nodo como V1, que es el voltaje del nodo 1 a tierra.
Paso 3: En la figura se establece que I1 e I2 abandonan el nodo, y se aplica la ley de
corriente de Kirchhoff de la siguiente forma:
La corriente I2 se relaciona con el voltaje nodal V1 mediante la ley de Ohm:
La corriente I1 también está determinada por la ley de Ohm de la siguiente forma:
Al sustituir en la ecuación de la ley de corriente de Kirchhoff:

10. y reagrupando, se tiene:
Al sustituir los valores numéricos, se obtiene:
Las corrientes I1 e I2 pueden determinarse entonces utilizando las ecuaciones anteriores:
El signo negativo indica simplemente que la corriente I1 opuesta a la que aparece en la figura
tiene una dirección