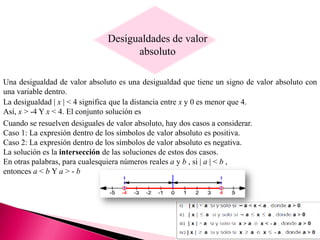
Los números reales incluyen números racionales e irracionales y pueden representarse en la recta numérica. Se pueden clasificar en números naturales, enteros, racionales e irracionales. Los números reales tienen un orden y podemos representar desigualdades entre ellos usando símbolos como <, > y valor absoluto.

1. María de los Angeles
Gonzalez
sección: 0100

2. El conjunto de los números reales se forma al combinar el conjunto de
números racionales y el conjunto de números irracionales. El conjunto
de números reales consiste en todos los números que tienen un lugar en
la recta numérica.
Definición
Números naturales 1, 2, 3, …
Números completos 0, 1, 2, 3, …
Enteros …, -3, -2, -1, 0, 1, 2, 3, …
Números racionales cualquier número que pueda ser
expresado de la forma donde p y q son enteros, los números racionales
terminan o se repiten cuando son escritos en forma decimal
Números irracionales cualquier número que pueda ser expresado de la
forma, (donde p y q son enteros), los números irracionales no terminan y no se repiten cuand
son escritos en forma decimal
Números reales cualquier número que sea racional o irracional

3. En los conjuntos se pueden realizar algunas operaciones básicas, que
parten de algunos conjuntos dados y se obtienen nuevos conjuntos.
Sean dos conjuntos, A y B del conjunto universal U.
Unión de conjuntos: La unión de dos conjuntos A y B, que se escribe A U B,
se define como el conjunto formado por los elementos comunes y no comunes a ambos conjuntos
Las uniones las podemos representar en diagramas de Venn de la siguiente forma;
1- Cuando los dos conjuntos tienen elementos en común la unión se representa de la siguiente
forma;

4. Los números reales son cualquier número que corresponda a un punto en la recta real y
pueden clasificarse en números naturales, enteros, racionales e irracionales. Es decir,
cualquier número real está comprendido entre menos infinito y más infinito y podemos
representarlo en la recta real
Número real
Orden
Todos los números reales tienen un orden:
En el caso de las fracciones y decimales:

5. desigualdad
En matemáticas, una desigualdad es
una relación de orden que se da entre dos
valores cuando estos son distintos (en caso
de ser iguales, lo que se tiene es
una igualdad).
Valor absoluto
En matemáticas, el valor absoluto o módulo​ de un
número real es su valor numérico sin tener en
cuenta su signo, sea este positivo o negativo.​ Así, 3
es el valor absoluto de +3 y de -3. El valor absoluto
está vinculado con las nociones de magnitud,
distancia y norma en diferentes contextos
matemáticos y físicos

6. Desigualdades de valor
absoluto
Una desigualdad de valor absoluto es una desigualdad que tiene un signo de valor absoluto con
una variable dentro.
La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor que 4.
Así, x > -4 Y x < 4. El conjunto solución es
Cuando se resuelven desiguales de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
La solución es la intersección de las soluciones de estos dos casos.
En otras palabras, para cualesquiera números reales a y b , si | a | < b ,
entonces a < b Y a > - b

8. https://content.nroc.org/Algebra.HTML5/U12L1T1/TopicText/es/text.html#:~:text=El%20conjunto%20de%2
0los%20n%C3%BAmeros%20reales%20se%20forma%20al%20combinar,lugar%20en%20la%20recta%20n
um%C3%A9rica.&text=Enteros%20%E2%80%A6%2C%20%2D3%2C%20%2D,1%2C%202%2C%203%2
C%20%E2%80%A6
https://economipedia.com › definiciones › números-reales
https://www.portaleducativo.net/cuarto-medio/24/Conjuntos