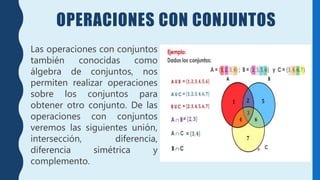
Este documento define conceptos básicos de conjuntos y números reales. Introduce conjuntos como agrupaciones de elementos que comparten propiedades, y describe operaciones comunes con conjuntos como unión, intersección, diferencia y complemento. Luego define números reales como cualquier número en la recta numérica entre -∞ y +∞, y clasifica números reales en naturales, enteros, racionales e irracionales. Finalmente, explica desigualdades y el valor absoluto de números reales.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN
UNIVERSIDAD POLITECNICA TERRITORIAL ANDRÉS ELOY BLANCO
BARQUISIMETO – ESTADO LARA
CONJUNTOS
MARÍA GIL
SECCIÓN: AD0105

2. DEFINICIÓN DE CONJUNTOS
Un conjunto es la agrupación
de diferentes elementos que
comparten entre sí
características y propiedades
semejantes. Estos elementos
pueden ser sujetos u objetos,
tales como números,
canciones, meses, personas,
etc. Por ejemplo: el conjunto
de números primos o el
conjunto de planetas del
sistema solar.

3. OPERACIONES CON CONJUNTOS
Las operaciones con conjuntos
también conocidas como
álgebra de conjuntos, nos
permiten realizar operaciones
sobre los conjuntos para
obtener otro conjunto. De las
operaciones con conjuntos
veremos las siguientes unión,
intersección, diferencia,
diferencia simétrica y
complemento.

4. UNIÓN DE CONJUNTOS
Es la operación que nos permite unir dos o más conjuntos para formar otro conjunto que
contendrá a todos los elementos que queremos unir pero sin que se repitan. Es decir dado un
conjunto A y un conjunto B, la unión de los conjuntos A y B será otro conjunto formado por
todos los elementos de A, con todos los elementos de B sin repetir ningún elemento.
Ejemplo
Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la
unión de estos conjuntos será
A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando diagramas de
Venn se tendría lo siguiente:
También se puede graficar del siguiente modo:

5. INTERSECCIÓN DE CONJUNTOS
Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la
operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los
elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El
símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.
Ejemplo
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
intersección de estos conjuntos será A∩B={4,5}. Usando
diagramas de Venn se tendría lo siguiente:
Ejemplo
Dados dos conjuntos A={x/x estudiantes que juegan fútbol} y B={x/x estudiantes
que juegan básquet}, la intersección será F∩B={x/x estudiantes que juegan
fútbol y básquet}. Usando diagramas de Venn se tendría lo siguiente:

6. DIFERENCIA DE CONJUNTOS
Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que
tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la
diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El
símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente: -.
Ejemplo
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
diferencia de estos conjuntos será A-B={1,2,3}. Usando
diagramas de Venn se tendría lo siguiente:
Ejemplo
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
diferencia de estos conjuntos será B-A={6,7,8,9}. Usando
diagramas de Venn se tendría lo siguiente:

7. DIFERENCIA DE SIMÉTRICA DE CONJUNTOS
Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto
resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir
dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no
comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia
simétrica es el siguiente: △.
Ejemplo
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia
simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando
diagramas de Venn se tendría lo siguiente:
Ejemplo
Dados dos conjuntos F={x/x estudiantes que juegan fútbol} y B={x/x
estudiantes que juegan básquet}, la diferencia simétrica será F △
B={x/x estudiantes que sólo juegan fútbol y básquet}. Usando
diagramas de Venn se tendría lo siguiente:

8. COMPLEMENTO DE UN CONJUNTO
Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no
están en el conjunto. Es decir dado un conjunto A que esta incluido en el conjunto universal U, entonces el conjunto
complemento de A es el conjunto formado por todos los elementos del conjunto universal pero sin considerar a los
elementos que pertenezcan al conjunto A. En esta operación el complemento de un conjunto se denota con un apostrofe
sobre el conjunto que se opera, algo como esto A' en donde el conjunto A es el conjunto del cual se hace la operación de
complemento.
Ejemplo
Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los
siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente:

9. NÚMEROS REALES
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden
clasificarse en números naturales, enteros, racionales e irracionales. En otras palabras, cualquier número
real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real. Los números
reales son todos los números que encontramos más frecuentemente dado que los números complejos no se
encuentran de manera accidental, sino que tienen que buscarse expresamente.
Los números reales se representan mediante la letra R ↓
Dominio de los números reales
Entonces, tal y como hemos dicho, los números reales son los números comprendidos entre los extremos infinitos. Es decir, no incluiremos estos infinitos en el conjunto.
Dominio de los números reales.
Números reales en la recta real
Esta recta recibe el nombre de recta real dado que podemos representar en ella todos los números reales. Línea real:

10. CLASIFICACIÓN DE LOS NÚMEROS REALES
•Números naturales
Los números naturales es el primer conjunto de números que
aprendemos de pequeños. Este conjunto no tiene en cuenta el
número cero (0) excepto que se especifique lo contrario (cero
neutral).
Expresión:
•Números enteros
Los números enteros son todos los números naturales e incluyen el
cero (0) y todos los números negativos.
Expresión:
•Números racionales
Los números racionales son las fracciones que pueden formarse a
partir de los números enteros y naturales. Entendemos las fracciones
como cocientes de números enteros.
Expresión:
•Números irracionales
Los números irracionales son números decimales que no pueden
expresarse ni de manera exacta ni de manera periódica.
Expresión:

11. EJEMPLOS DE NUMEROS REALES
En el siguiente ejemplo sobre los números reales, comprueba que los siguientes números
corresponden a punto en la recta real.
•Números naturales: 1,2,3,4…
•Números enteros: …,-4,-3,-2,-1, 0, 1, 2, 3, 4…
•Números racionales: cualquier fracción de números enteros.
•Números irracionales:

12. DESIGUALDADES DE NUMEROS
REALES
En matemáticas, una desigualdad es una relación de orden que se da entre dos valores
cuando estos son distintos (en caso de ser iguales, lo que se tiene es una igualdad).
Si los valores en cuestión son elementos de un conjunto ordenado, como los enteros o
los reales, entonces pueden ser comparados.
• La notación a < b significa a es menor que b;
• La notación a > b significa a es mayor que b

13. DESIGUALDADES DE NUMEROS REALES
Estas relaciones se conocen como desigualdades estrictas, puesto que a no puede ser
igual a b; también puede leerse como "estrictamente menor que" o "estrictamente
mayor que“
La notación a ≤ b significa a es menor o igual que b;
La notación a ≥ b significa a es mayor o igual que b;
estos tipos de desigualdades reciben el nombre de desigualdades amplias (o no
estrictas).
La notación a ≪ b significa a es mucho menor que b;
La notación a ≫ b significa a es mucho mayor que b; esta relación indica por lo
general una diferencia de varios órdenes de magnitud.
La notación a ≠ b significa que a no es igual a b. Tal expresión no indica si uno es
mayor que el otro, o siquiera si son comparables.

14. DEFINICIÓN DE VALOR ABSOLUTO
La noción de valor absoluto se utiliza en el terreno de las matemáticas para nombrar al valor que tiene
un número más allá de su signo. Esto quiere decir que el valor absoluto, que también se conoce
como módulo, es la magnitud numérica de la cifra sin importar si su signo es positivo o negativo.
Ejemplo: 3 es el valor absoluto de +3 y de -3.
El valor absoluto está vinculado con las nociones de magnitud, distancia y norma en diferentes contextos
matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos
otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

15. DESIGUALDADES CON VALOR ABSOLUTO
Una desigualdad de valor absoluto es una desigualdad que tiene un signo de valor absoluto con
una variable dentro.
Desigualdades de valor absoluto (<):
La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor que 4.
Así, x > -4 Y x < 4. El conjunto solución es
.
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
La solución es la intersección de las soluciones de estos dos casos.
En otras palabras, para cualesquiera números reales a y b , si | a | < b , entonces a < b Y a > - b .