Descargado 148 veces
Subido porCAChemE
Optimizacion con Python (Pyomo vs GAMS vs AMPL)
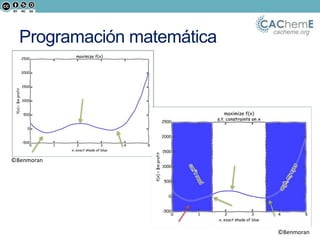
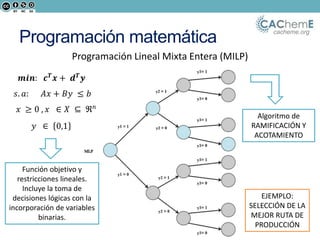
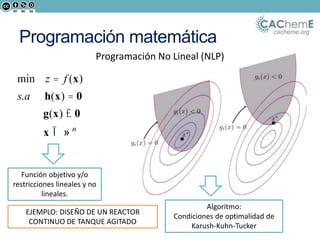
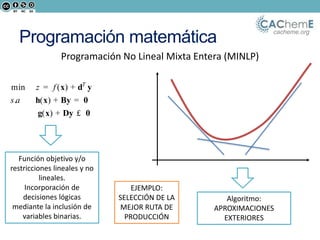
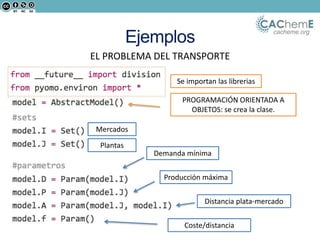
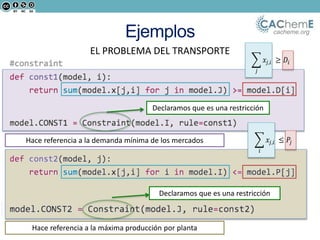
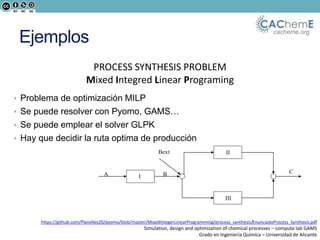
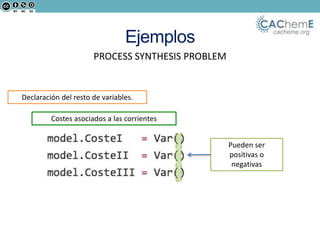
El documento aborda la optimización matemática en ingeniería química, centrándose en el uso de Python y herramientas como Pyomo para resolver diversos problemas de optimización, incluyendo programación lineal y no lineal. Se discute la importancia de la optimización para mejorar la calidad de productos, reducir costos y minimizar riesgos ambientales, y se presentan ejemplos prácticos de problemas de transporte y síntesis de procesos. Además, se detallan lenguajes de modelado algebraico y diferentes algoritmos utilizados en estos procesos.
Más contenido relacionado
Similar a Optimizacion con Python (Pyomo vs GAMS vs AMPL)
Optimizacion con Python (Pyomo vs GAMS vs AMPL)
- 1. Computer-aided Chemical Engineering www.cacheme.org Chem.Engineer Daniel Domene Python en la industria: el problema de optimización (matemática) Carlos Planelles Chem. Engineering Student
- 2. Índice • Programación matemática •AML (Algebraic Modeling Languages) • Optimización en Python: ¿Por qué Pyomo? • Ejemplos • Bibliografía www.cacheme.org
- 3. Índice • Programación matemática •AML (Algebraic Modeling Languages) • Optimización en Python: ¿Por qué Pyomo? • Ejemplos • Bibliografía www.cacheme.org
- 4. cacheme.org Programación matemáticacacheme.org n matemática ón:¿por qué es importante? producto entales ducción uipos y recursos a Interés empresarial (cc) Sam Derbyshire Optimización: ¿por qué es importante? • Mejorar la calidad de un producto • Aumentar beneficios • Reducir riesgos ambientales • Reducir costes de producción • Etc. En la Ingeniería Química Selección de equipos Gestión logística …
- 5.
- 6. cacheme.org Programación matemática Problemas deoptimización • Programación Lineal (LP) • Programación Lineal Mixta Entera (MILP) • Programación No Lineal (NLP) • Programación No Lineal Mixta Entera (MINLP)
- 7. cacheme.org Programación matemática Programación Lineal(LP) Función objetivo y restricciones lineales Algoritmo de SIMPLEX EJEMPLO: PROBLEMA DEL TRANSPORTE
- 8. cacheme.org Programación matemática Programación LinealMixta Entera (MILP) Función objetivo y restricciones lineales. Incluye la toma de decisiones lógicas con la incorporación de variables binarias. Algoritmo de RAMIFICACIÓN Y ACOTAMIENTO EJEMPLO: SELECCIÓN DE LA MEJOR RUTA DE PRODUCCIÓN 𝒎𝒊𝒏: 𝒄 𝑻 𝒙 + 𝒅 𝑻 𝒚 𝑠. 𝑎: 𝐴𝑥 + 𝐵𝑦 ≤ 𝑏 𝑥 ≥ 0 , 𝑥 ∈ 𝑋 ⊆ ℜ 𝑛 𝑦 ∈ 0,1
- 9. cacheme.org min z =f (x) s.a h(x) = 0 g(x) £ 0 x Î » n Programación matemática Programación No Lineal (NLP) Función objetivo y/o restricciones lineales y no lineales. Algoritmo: Condiciones de optimalidad de Karush-Kuhn-Tucker EJEMPLO: DISEÑO DE UN REACTOR CONTINUO DE TANQUE AGITADO
- 10. cacheme.org { } ) + )+ ) + min ( . ( ( , 0,1 : , : , : , , T mn n n l n p m l m p m z f s a f ´ ´ = = £ Î Î ® ® ® Î Î Î ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ x d y h x By 0 g x Dy 0 x y h g d B D Programación matemática Programación No Lineal Mixta Entera (MINLP) Función objetivo y/o restricciones lineales y no lineales. Incorporación de decisiones lógicas mediante la inclusión de variables binarias. Algoritmo: APROXIMACIONES EXTERIORES EJEMPLO: SELECCIÓN DE LA MEJOR RUTA DE PRODUCCIÓN
- 11. Índice • Programación matemática •AML (Algebraic Modeling Languages) • Optimización en Python: ¿Por qué Pyomo? • Ejemplos • Bibliografía www.cacheme.org
- 12. cacheme.org AML (Algebraic modellinglanguages) Software propietario: AMPL (www.ampl.com) Lenguaje sencillo, pero complicado interactuar - GLPK es una alternativa libre para LP y MILP GAMS (www.gams.com) Se comunica con solvers incluso para resolver MINLP AIMMS (www.aiims.com) Diseñado para resolver problemas de optimización a gran escala, y programación de actividades.
- 13. cacheme.org Optimización en Python:¿Por qué Pyomo? Free Open source: CVXOPT – M. Andersen, J. Dahl, L. Vandenberghe Notación matricial. Optimización Convexa PuLP – Trabaja con lenguaje Python. Muy buenos resultados para LP y MILP. No resuelve NLP OpenOpt – Más de 30 solvers para solucionar el modelado, incluyendo programación no lineal. Pyomo – Coopr. (Sandia National Laboratories, USA) Permite la formulación de modelos algebraicos en Python.
- 14. cacheme.org • Se comunicadirectamente con los principales solvers de AMPL, GLPK, Gurobi, CPLEZ, CBC y PICO. • Programación en Python tipo AMPL/GAMS. • Compatible con Python 2 y 3. • Pyomo (Coopr) es un paquete gratuito con licencia BSD, maduro y bien documentado. • Fácil instalación “pip install pyomo”, instalación de solver aparte. • Adaptabilidad a modelado de la mayoría de problemas.cacheme.org ¿Por qué Pyomo? Se comunica directamente los principales solvers de AMPL, GLPK, Gurobi, CPLEX, CBC y PICO. Programación en Python tipo AMPL/GAMS Open source (COIN-OR) coin-or.org Optimización en Python: ¿Por qué Pyomo?
- 15. Índice • Programación matemática •AML (Algebraic Modeling Languages) • Optimización en Python: ¿Por qué Pyomo? • Ejemplos • Bibliografía www.cacheme.org
- 16. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Linear Programing • Problema clásico de optimización LP • Se puede resolver con GLPK • Hay que minimizar el coste en el transporte del producto
- 17. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Linear Programing A1# A2# C1# C2# C3# x2# y2# z2# x1# y1# z1# C3 C2
- 18. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Linear Programing A1 A2 C1 C3 C2 0.1 0.7 0.8 0.3
- 19. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE PROGRAMACIÓN ORIENTADA A OBJETOS: se crea la clase. Se importan las librerias Mercados Plantas Demanda mínima Producción máxima Coste/distancia Distancia plata-mercado
- 20. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Se nombran las variables, que corresponderán con la cantidad de producto desde una planta a un mercado. No puede ser negativaDepende de las plantas y los mercados. Declaramos que es una variable
- 21. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Por defecto minimiza. (Para maximizar teclear maximize) Declaramos que es la función a optimizar
- 22. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Declaramos que es una restricción Declaramos que es una restricción Hace referencia a la demanda mínima de los mercados Hace referencia a la máxima producción por planta
- 23. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Archivo con los datos del problema: Exigencias de los mercados, costes por transporte… Mercados Plantas Demanda mínima Producción máxima Coste/distancia Distancia plata-mercado
- 24. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Linear Programing
- 25. cacheme.org Ejemplos EL PROBLEMA DELTRANSPORTE Cantidad de producto de cada planta al correspondie nte mercado Coste total
- 26. cacheme.org Ejemplos PROCESS SYNTHESIS PROBLEM MixedIntegred Linear Programing • Problema de optimización MILP • Se puede resolver con Pyomo, GAMS… • Se puede emplear el solver GLPK • Hay que decidir la ruta optima de producción The goal is to maximize profits. Consider the following two cases: 1- The maximum demand for C is 10 tons / h, with a selling price of 1800 Euros / ton. 2- The maximum demand for C is 15 ton / h, the sale price is 1800 Euros / ton for the first 10 ton and 1500 Euros / ton for excess. Capital and operational costs Fixed cost (Euros / h.) Variable (Euros / ton of raw material entering the process) Process I 1000 250 Process II 1500 400 Process III 2000 550 Prices A 500 Euros / ton. B 950 Euros / ton. Conversion Process I 90 % from A to B Process II 82 % from B to C Process III 95 % from B to C Maximum availability for A: 16 ton / h. Solve again the problem for the case where the input-ouput relationships for process II and III are given by the following equations: Proceso II: C = 6.5 Ln(1+B) I II III A Bext CB https://github.com/Planelles20/pyomo/blob/master/MixedIntegerLinearProgramming/process_synthesis/EnunciadoProcess_Synthesis.pdf Simulation, design and optimization of chemical processes – compute lab GAMS Grado en Ingeniería Química – Universidad de Alicante
- 27. cacheme.org Ejemplos PROGRAMACIÓN ORIENTADA A OBJETOS:se genera el modelo. Se cargan los operadores y la biblioteca numpy Variables binarias del sistema para toma de decisiones lógicas ( 0 , 1 ) 0: No proceso I , 1: Si proceso I 0: No proceso II , 1: Si proceso II 0: No proceso III , 1: Si proceso III PROCESS SYNTHESIS PROBLEM
- 28. cacheme.org Ejemplos Declaración del restode variables. Unidades de producción que circulan por las corrientes Físicamente no pueden ser negativas PROCESS SYNTHESIS PROBLEM
- 29. cacheme.org Ejemplos Declaración del restode variables. Costes asociados a las corrientes Pueden ser positivas o negativas PROCESS SYNTHESIS PROBLEM
- 30. cacheme.org Ejemplos Declaración de lasrestricciones PROCESS SYNTHESIS PROBLEM
- 31. cacheme.org Ejemplos Declaración de lasrestricciones PROCESS SYNTHESIS PROBLEM
- 32. cacheme.org Ejemplos Declaración de lasrestricciones PROCESS SYNTHESIS PROBLEM El proceso II y III son excluyentes, por lo se introduce esta restricción para que en el resultado final solo se escoja uno de los dos El problema también establece unos valores máximos para ciertas variables, por lo que se ha de tener en cuenta con estas restricciones de límite superior.
- 33. cacheme.org Ejemplos FUNCIÓN OBJETIVO PROCESS SYNTHESISPROBLEM Tiene en cuenta los beneficios de venta del producto final y el coste de los productos y de producción
- 34.
- 35. cacheme.org Ejemplos PROCESS SYNTHESIS PROBLEM Existeel proceso IIExiste el proceso I “Es más barato producir B que comprarlo”
- 36. cacheme.org rices A 500Euros / ton. B 950 Euros / ton. onversion Process I 90 % from A to B Process II 82 % from B to C Process III 95 % from B to C Maximum availability for A: 16 ton / h. again the problem for the case where the input-ouput relationships for process II and III are given by the wing equations: Proceso II: C = 6.5 Ln(1+B) Proceso III: C= 7.2 Ln(1+B) e B y C are the mass flow rate (ton/h) for B y C, respectively. I II III A Bext CB Ejemplos PROCESS SYNTHESIS PROBLEM or excess. Capital and operational costs Fixed cost (Euros / h.) Variable (Euros / ton of raw material entering the process) rocess I 1000 250 rocess II 1500 400 rocess III 2000 550 rices A 500 Euros / ton. B 950 Euros / ton. onversion Process I 90 % from A to B Process II 82 % from B to C Process III 95 % from B to C Maximum availability for A: 16 ton / h. I II III A Bext CB Caso de estudio Caso para cuando aumenta la producción y el exceso de C es menos rentable or excess. Capital and operational costs Fixed cost (Euros / h.) Variable (Euros / ton of raw material entering the process) rocess I 1000 250 rocess II 1500 400 rocess III 2000 550 rices A 500 Euros / ton. B 950 Euros / ton. onversion Process I 90 % from A to B Process II 82 % from B to C Process III 95 % from B to C Maximum availability for A: 16 ton / h. I II III A Bext CB
- 37. cacheme.org Ejemplos REACTOR DESIGN Non LinearProgramming • Problema NLP • Problema típico en la industria química • Se puede resolver con ipopt • Hay que maximizar la producción de B, atendiendo a la velocidad espacial https://en.wikipedia.org/wiki/Continuous_stirred-tank_reactor Carl D. Laid Chemical Engineer
- 38. cacheme.org Ejemplos REACTOR DESIGN Se carganlos datos del problema Coeficientes de reacción y concentración inicial de reactivo PROGRAMACIÓN ORIENTADA A OBJETOS: se crea la clase
- 39. cacheme.org REACTOR DESIGN Ejemplos Se creanlas variables Se aporta un valor inicial de las variables para facilitar el cálculo Físicamente no pueden ser negativas Concentraciones de las especies
- 40. cacheme.org REACTOR DESIGN Ejemplos RESTRICCIONES ESTADO ESTACIONARIO Balancede componente A Balance de componente B Tiempo de residencia
- 41. cacheme.org REACTOR DESIGN Ejemplos RESTRICCIONES ESTADO ESTACIONARIO Balancede componente C Balance de componente B
- 42. cacheme.org REACTOR DESIGN Ejemplos RESTRICCIONES Función objetivo Maximizarla concentración de B
- 43. cacheme.org Bibliografía • Apuntes dela asignatura Simulación y Optimización de procesos Industriales del Grado en Ingeniería Química de la Universidad de Alicante. • Pyomo – Optimization modeling in Python • Springer Optimization and its aplications Vol. 67. Willian E. Hart • Sandia National Laboratories Agradecimientos • Dr. Rubén Ruiz-Femenia • Dr. Ignacio Aracil • Francisco J. Navarro-Brull
- 44. @CAChemEorg CAChemEorg CAChemE info@cacheme.orgmail www.cacheme.org Muchas gracias porsu atención Chem. Engineer Chem. Engineering Student Daniel Domene Carlos Planelles https://github.com/CAChemE/pyomo
Notas del editor
- #7 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #8 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #9 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #11 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #13 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #14 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #15 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #17 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #18 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #19 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #20 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #21 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #22 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #23 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #24 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #25 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #26 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #27 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #28 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #29 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #30 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #31 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #32 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #33 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #34 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #35 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #36 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #37 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #38 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #39 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #40 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #41 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #42 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #43 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m
- #44 La forma más común para representar un problema de optimización matemática es el dado por una función objetivo y un conjunto de funciones de restricción. f x,y s.a: g x,y≤0 h x,y= 0 x ∈X ⊆ Rn y ∈ 0,1m