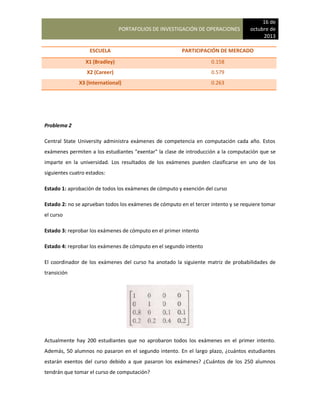
El documento detalla el plan del curso de Investigación de Operaciones para la licenciatura en Ingeniería Industrial en la Universidad Tecnológica de Panamá, que incluye temas como programación dinámica, modelos de optimización de inventarios, teoría de colas y simulación. Su objetivo es proporcionar herramientas cuantitativas para la toma de decisiones en situaciones de complejidad e incertidumbre. Además, se describen los métodos de evaluación, bibliografía recomendada y recursos didácticos.





























































































![PORTAFOLIOS DE INVESTIGACIÓN DE OPERACIONES
16 de
octubre de
2013
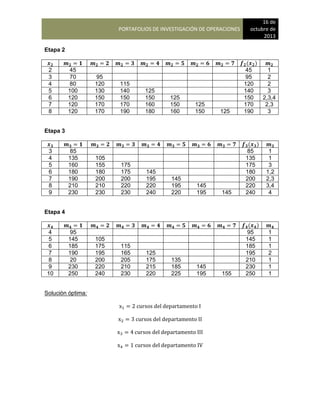
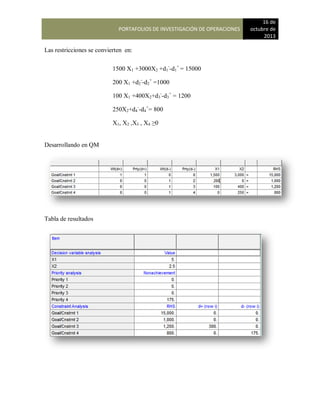
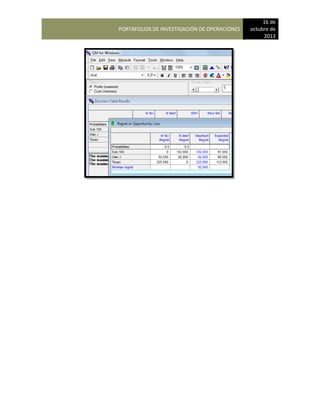
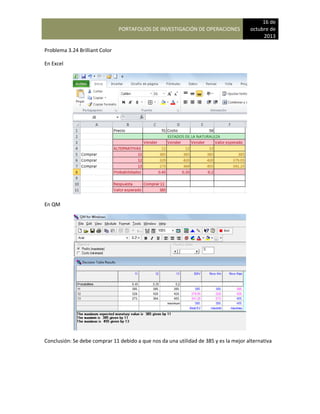
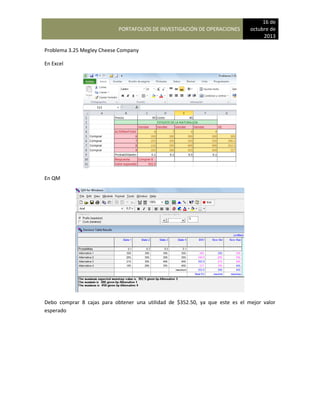
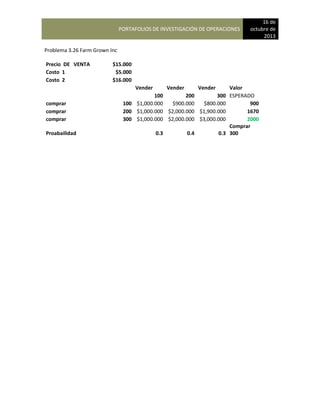
Estado 2 participación inicial = 0.35-Career Academy
Estado 3 participación inicial = 0.25-International Technology
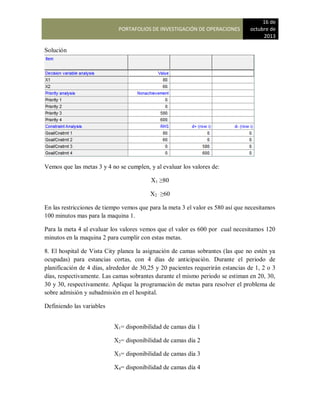
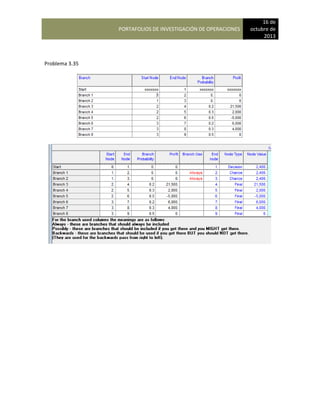
Los valores de la matriz de transición son:
A
DE 1 Bradley 2 Careff 3 International
1 Bradley 0.65 0.20 0.15
2 Careff 0.05 0.90 0.05
3 International 0.10 0.10 0.80
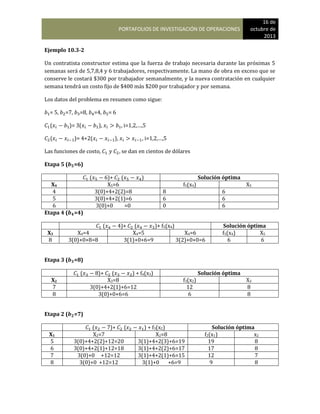
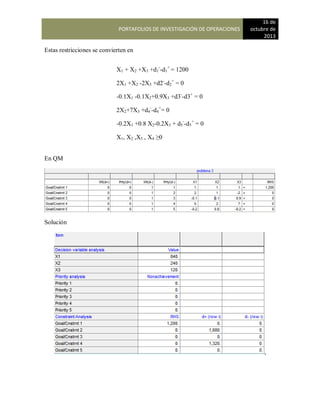
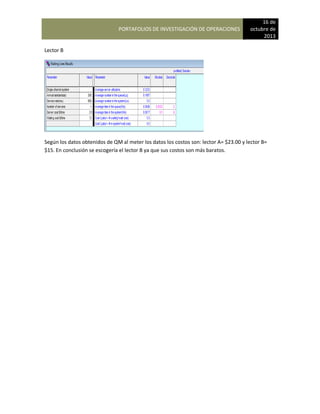
Para que George determine la participación de mercado de Bradley School durante el próximo año
que multiplicar las participaciones de mercado actual por la matriz de probabilidades de
continuación se muestra la estructura general de estos cálculos:
{0.40 0.35 0.25) [0.65 0.20 0.15]
0.05 0.90 0.05
0.10 0.10 0.80
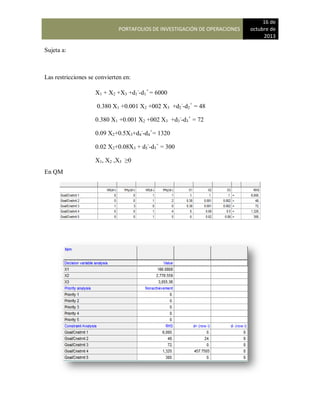
En consecuencia, la participación de mercado de Bradley School, International Academy puede
calcularse multiplicando las participaciones de mercado actual por las probabilidades la matriz de
transición, tal como se muestra. El resultado será una nueva matriz con uno de los cuales
representa la participación de mercado de una de las escuelas. Los cálculos de la matriz son los
siguientes:
Participación de mercado de Bradley School = (0.40) (0.65) + (0.35) (0.05) + (0.25) (0.10) = 0.303
Participación de mercado de Career Academy = (0.40) (0.20) + (0.35) (0.90) + (0.25) (0.10)= 0.420
Participación de mercado de International Technology = (0.40) (0.15) + (0.35) 0.05+ (0.25) (0.10)=
0.278](https://image.slidesharecdn.com/pdf-230104183256-ebd555a4/85/INVESTIGACION-DE-OPERACIONES-notas-123-320.jpg)