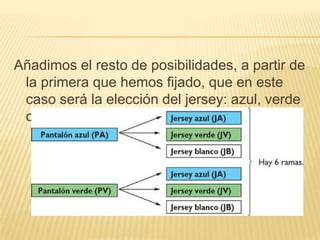
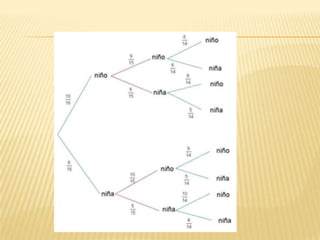
Este documento describe diferentes métodos para contar resultados posibles en un espacio muestral, incluyendo tablas de multiplicación, diagramas de árbol y permutaciones. Explica cómo usar estos métodos para calcular el número de almuerzos posibles con diferentes opciones, el número de formas en que un cliente puede elegir un camión con diferentes colores y motores, y el número de maneras de marcar un artículo que pasa por tres controles de calidad.

1. Oscar Torres Rivera
PROBABILIDAD

2. MÉTODOS DE CONTEO
Cuando se calculan las probabilidades algunas veces se
necesita determinar el numero e resultados en un
espacio neutral. En esta sección se describirá diversos
métodos con ese propósito . La regla básica que se
conoce principio fundamental.

3. Al generalizar el ejemplo si hay N1 elecciones
de color y N2 de motor una lista completa
de elecciones se puede escribir como una
tabla N1 X N2 Por lo que el numero total de
elecciones N1N2 .

4. Ejemplo ¿Cuántos almuerzos que consisten en
una sopa, emparedado, postre
y una bebida son posibles si podemos
seleccionar de 4 sopas, 3 tipos de
emparedados, 5 postres y 4 bebidas?
Como n1 = 4, n2 = 3, n3 = 5 y n4 = 4
hay en total
n1 X n2 X n3 X n4 = 4 X 3 X 5 X 4 = 240
almuerzos diferentes para

5. DE MÉTODO DE CONTEO
Cierto tipo de camión es encontrado disponible en tres
colores : rojo, amarillo verde. Puede tenerse un motor
grande o pequeño .
¿de cuantos modos puede un cliente elegir un coche ?
Hay tres opciones de color y dos opciones de motor

6.  Una lista completa muestra de las opciones
que se muestra en la siguiente es de 3x2 el
no muero total de opciones (3) (2) =6
Rojo Amarillo verde
Rojo grande Amarillo grande Verde grande
Rojo pequeño Amarillo pequeño Verde pequeño

7. EJEMPLO
 Ejemplo: Un artículo manufacturado debe pasar por
tres controles. En cada
 uno de ellos se inspecciona una característica
particular del artículo y se le
 marca de conformidad. En el primer control hay tres
mediciones posibles,
 mientras que en cada uno de los dos últimos
controles hay cuatro
 mediciones posibles. Por lo tanto, hay 3 ⋅ 4 ⋅ 4 = 48
maneras de marcar el
 artículo.

8. DIAGRAMAS DE ÁRBOL
 Un diagrama de árbol es una herramienta
que se utiliza para determinar todos los
posibles resultados de un experimento
aleatorio. En el cálculo de la probabilidad se
requiere conocer el número de elementos
que forman parte del espacio muestra, estos
se pueden determinar con la construcción
del diagrama de árbol.

9.  El diagrama de árbol es una representación
gráfica de los posibles resultados del
experimento, el cual consta una serie de
pasos, donde cada uno de los pasos tiene
un número finito de maneras de ser llevado a
cabo. Se utiliza en los problemas de conteo
y probabilidad.

10. Para la construcción de un diagrama en árbol
se partirá poniendo una rama para cada una
de las posibilidades, acompañada de su
probabilidad. Cada una de esta ramas se
conoce como rama de primera generación

11. Añadimos el resto de posibilidades, a partir de
la primera que hemos fijado, que en este
caso será la elección del jersey: azul, verde
o blanco.

12. Una clase consta de seis niñas y 10 niños. Si
se escoge un comité de tres al azar, hallar la
probabilidad de:
1 Seleccionar tres niños.

14. Seleccionar exactamente dos niños y una niña.
Seleccionar exactamente dos niñas y un niño.

15. PERMUTACIONES
 En matemáticas, llamamos permutación de un
conjunto a cada una de las posibles
ordenaciones de todos los elementos de dicho
conjunto.
 Por ejemplo, en el conjunto {1,2,3}, cada
ordenación posible de sus elementos, sin
repetirlos, es una permutación. Existe un total
de 6 permutaciones para estos elementos:
"1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".

16.  1. ¿Cuántos números de 5 cifras diferentes se
puede formar con los dígitos: 1, 2, 3, 4, 5.?
m=5 n=5
 Sí entran todos los elementos. De 5 dígitos
entran sólo 3.
 Sí importa el orden. Son números distintos el
123, 231, 321.
 No se repiten los elementos. El enunciado nos
pide que las cifras sean diferentes.
p5 =5!=5.4.3.2.1= 120

17.  ¿De cuántas formas distintas pueden
sentarse ocho personas en una fila de
butacas?
 Sí entran todos los elementos. Tienen que
sentarse las 8 personas.
 Sí importa el orden.
 No se repiten los elementos. Una persona
no se puede repetir.

18. ¿De cuántas formas distintas pueden sentarse
ocho personas alrededor de una mesa
redonda?