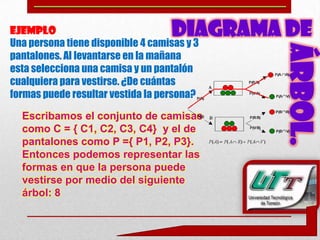
Este documento describe diferentes métodos de conteo como permutaciones, combinaciones y diagramas de árbol. Explica que las permutaciones cuentan los arreglos posibles de objetos tomados todos a la vez sin repetición, mientras que las combinaciones cuentan los arreglos sin importar el orden. También describe el principio de la multiplicación para contar múltiples opciones y provee ejemplos de su aplicación.

1. 2
MÉTODOS DE
CONTEO
¨A
PROCESOS INDUSTRIALES
ÁREA MANUFACTURA

2. Las técnicas de conteo son aquellas que son
usadas para enumerar eventos difíciles de
cuantificar métodos para determinar sin
tener que numerar directamente el número
de resultados posibles de un experimento
particular o el número de los elementos de
un conjunto en particular, también se le
conoce como análisis combinatorio.

3. PRINCIPIO DE LA MULTIPLICACIÓN
Métodos de conteo, regla de la multiplicación la cual
dice que si una operación se puede llevar a cabo en 1
n formas y si para cada una de estas se puede
realizar una segunda operación en 2 n y para cada
una de dos primeras se puede realizar una tercera
operación 3 n formas, y así sucesivamente, entonces
la serie de k operaciones se puede realizar en n n ,...,
n k 1 2 formas.

4. PRINCIPIO DE LA MULTIPLICACIÓN
Ejemplo
¿Cuántos almuerzos que consisten en una
sopa, emparedado, postre y una bebida son posibles si
podemos seleccionar de 4 sopas, 3 tipos de
emparedados, 5 postres y 4 bebidas?
Solución:
Como 1 n = 4, 2 n = 3, 3 n = 5 y 4 n = 4 hay en
total.
1 n X 2 n X 3 n X 4 n = 4 X 3 X 5 X 4 = 240
almuerzos diferentes para elegir

5. PERMUTACIONES.
Una permutación de un número de
objetos es un arreglo de todas o una
parte de los objetos en un orden
definido.
1.- Permutaciones Lineales:
2.-Permutaciones de Objetos
Diferentes

6. PERMUTACIONES.
Una permutación es un arreglo de todo o parte de
un conjunto de objetos.
El número de permutaciones de n objetos
distintos es n!.
Ejemplo:
De cuantas maneras se pueden ubicar 6
personas en una fila.
7x 6x 5x 4x 3x 2x 1
7 x 6 x 5 x 4 x 3 x 2 x 1 = 7! = 5040.

7. PERMUTACIONES.
Permutaciones de diferentes objetos tomados todos a la vez.
El total de permutaciones de un conjunto de objetos tomados
todos a la vez, se obtiene razonando en forma similar del
principio fundamental de contar.
NPn=n!
PALABRAS
Ejemplo:
Cuantas palabras de cinco letras se pueden formar
con la palabra libro, aplique permutaciones.
5P5=5!= 5x4x3x2x1=120

8. PERMUTACIONES.
Una permutación de “n” objetos diferentes
tomados de “r” en “r” es también una
ordenación de “r” entre los “n” objetos.
Ejemplos:
Cuantas palabras de tres letras se pueden formar con
las letras de la palabra libro.
N= 5 R=3
Cuantos Números de dos dígitos se pueden formar con
los dígitos 4,6,9 y cuales son, sin repetirse los dígitos.
N= 3 R=2

9. COMBINACIONES Es cada uno de los diferentes arreglos que se
pueden hacer con parte o con todos los
elementos de un conjunto dado sin que ninguno
se repita y sin importar el orden de ellos.
Estas agrupaciones se diferencian entre
sí, sólo por los elementos que las conforman.
El número de combinaciones de n objetos
tomando r a la vez se denota C(n,r).

10. COMBINACIONES Ejemplo
De cuatro químicos y tres físicos encuentre el número de
comités que se pueden formar que consistan en dos
químicos y un físico.
Solución
El número de formas de seleccionar a dos
químicos, de cuatro es:
(4/2) = 4¡/2¡2¡ = 6
El número de formas de seleccionar un
físico, de tres es: (3/1) = 3¡/1¡2¡ = 3
Al usar la regla de la multiplicación tenemos
n = 6 y n = 3 , podemos formar:
(6)(3) = 18 Comités con 2 químicos y 1 físico.

11. DIAGRAMA DE
Un diagrama de árbol es una
ÁRBOL.
representación gráfica de un
experimento que consta de r
pasos, donde cada uno de los pasos
tiene un número finito de maneras
de ser llevado a cabo.

12. Ejemplo DIAGRAMA DE
Una persona tiene disponible 4 camisas y 3
ÁRBOL.
pantalones. Al levantarse en la mañana
esta selecciona una camisa y un pantalón
cualquiera para vestirse. ¿De cuántas
formas puede resultar vestida la persona?
Escribamos el conjunto de camisas
como C = { C1, C2, C3, C4} y el de
pantalones como P ={ P1, P2, P3}.
Entonces podemos representar las
formas en que la persona puede
vestirse por medio del siguiente
árbol: 8

13. MÉTODOS DE CONTEO
2
PROCESOS INDUSTRIALES
ÁREA MANUFACTURA ¨A
Julio_rmz10@hotmail.com
http://www.facebook.com/julio_rmz10@hotmail.com
http://jullio-rmz10.bligoo.com.mx/