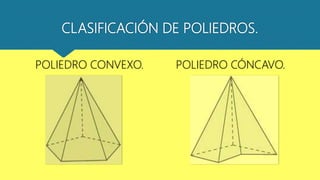
Este documento describe los poliedros, incluidos los sólidos platónicos y de Arquímedes. Los poliedros son sólidos de caras planas. Los sólidos platónicos son poliedros regulares y solo existen cinco: el tetraedro, el hexaedro (cubo), el octaedro, el dodecaedro y el icosaedro. Los trece sólidos de Arquímedes son poliedros con vértices idénticos y caras regulares como el cuboctaedro.

1. POLIEDROS.
“Los solidos Platónicos y de
Arquímedes.”
INTEGRANTES:
Gutiérrez López Carla B.
Ruedas canchola Marcelino de Jesús.
Valdivia Ruíz José Alejandro
PROFESOR: Arq. Juan Gabriel de la Torre Venegas.
Materia: Fundamentos Del Diseño III.
3°B. Lic. En arquitectura.

2. ¿Qué es un Poliedro?
Un poliedro es un sólido de caras planas.
MUCHAS - CARA.

3. ELEMENTOS DEL POLIEDRO:

4. PRISMA TRIÁNGULAR.

5. CUBO

6. DODECAEDRO.

7. CLASIFICACIÓN DE POLIEDROS.
POLIEDRO CONVEXO. POLIEDRO CÓNCAVO.

8. POLIEDROSSEGÚN
ELNÚMERODECARAS
NOMBRE CARACTERÍSTICAS
Tetraedro Poliedro de 4 caras.
Pentaedro Poliedro de 5 caras.
Hexaedro Poliedro de 6 caras
Heptaedro Poliedro de 7 caras.
Octaedro Poliedro de 8 caras.
Eneaedro Poliedro de 9 caras.
Decaedro Poliedro de 10 caras.
Endecaedro Poliedro de 11 caras.
Dodecaedro Poliedro de 12 caras
Tridecaedro Poliedro de 13 caras.
Tetradecaedro Poliedro de 14 caras.
Pentadecaedro Poliedro de 15 caras.
Icosaedro Poliedro de 20 caras.

9. CLASIFICACIÓN DE POLIEDROS SEGÚN SU
REGULARIDAD
POLIEDROS REGULARES.
Sólo existen cinco poliedros regulares:
1. Tetraedro
2. Hexaedro o cubo
3. Octaedro
4. Dodecaedro
5. Icosaedro

10.  Un poliedro irregular está definido por polígonos
que no son todos iguales.
POLIEDROS
IRREGULARES.

12. SÓLIDOS DE PLATÓN.
Un sólido platónico es un poliedro regular. En los sólidos platónicos, pues todas las caras
son iguales, lo que implica que
la sucesión de las mismas es invariante. Si un poliedro tiene todos sus
vértices iguales entre sí se dice que es de vértices uniformes.

13. O sea que…
Un poliedro regular es todo aquel poliedro convexo cuyas caras son
polígonos regulares iguales entre sí, y cuyos vértices son iguales

14. PROPIEDADES:
DIMENSIONES FUNDAMENTALES
En los sólidos platónicos como en cualquier poliedro existe una serie
de dimensiones que es importante conocer. Éstas son el área de la
superficie y el volumen del sólido

16. SIMETRÍA.
- Simetría puntual: Para cada uno de los 5 sólidos existe un punto, que es siempre el punto central del poliedro que
es el centro de simetría en la simetría puntual.
- Simetría axial: Todos los sólidos tienen además varios ejes de simetría. Para cada poliedro la cantidad varía; pero en
todos ellos el eje de simetría pasa por el centro de simetría.
- Simetría de plano: De nuevo todos los sólidos platónicos presentan simetrías respecto a planos, en las que los
planos de simetría contienen al centro de simetría, y a combinaciones de los ejes de simetría.

18. TRECE SÓLIDOS DE ARQUÍMEDES

19. SÓLIDOS DE ARQUÍMEDES.
Los Sólidos Arquimedianos son los únicos 13 poliedros convexos, con vértices idénticos y cuyas caras
son polígonos regulares.
Como todos los vértices son iguales entre ellos, estos sólidos se pueden describir indicando qué
polígonos regulares se unen en cada vértice y en qué orden.

20. CUBOCTAEDRO

21. Cinco de los Sólidos Arquimedianos se derivan de los Sólidos Platónicos por un proceso de truncado
(cortar las equinas) con un porcentaje inferior a 1/2. El porcentaje de truncado f varía en cada sólido; el
objetivo es obtener nuevos polígonos regulares como caras.

23. Hay otros dos Sólidos Arquimedianos especiales que pueden obtenerse truncando por completo
(f=1/2) dos Sólidos Platónicos duales cada uno de ellos: el Cuboctaedro, que proviene de truncar o
bien el Cubo o su dual el Octaedro. Y el Icosidodecaedro, que proviene de truncar el Icosaedro o su
dual el Dodecaedro. De aquí su "doble nombre.

24. El Rombicuboctaedro y el Rombicosidodecaedro, aparentemente parecen provenir de truncar los dos sólidos
precedentes.
Estos dos sólidos se construyen con otra técnica. En realidad se pueden construir a partir de los Sólidos
Platónicos originales mediante un proceso conocido como expansión. Este consiste en separar
progresivamente las caras del poliedro original con simetría esférica, hasta un punto en que se puedan unir
mediante nuevas caras que sean polígonos regulares. Este proceso se ilustra en la figura siguiente:

26. El nombre de Cuboctaedro Truncado (también llamado Gran Rombicuboctaedro) y el de
Icosidodecaedro Truncado (también conocido como Gran Rombicosidodecaedro) parecen indicar
que estos sólidos se derivan de truncar el Cuboctaedro y el Icosidodecaedro. Pero tal como
acabamos de razonar esto no es posible.

27. Por último, existen otros dos sólidos especiales que tienen dos formas o variaciones quirales (simetría
especular): el Cubo romo y el Dodecaedro romo. Aquí mostramos sólo una de las formas quirales de
cada uno de ellos:

28. Estos sólidos pueden construirse por alternancia de otro Sólido Arquimediano. Este proceso consiste en eliminar
vértices alternos y crear nuevos triángulos en los vértices eliminados. La figura siguiente ilustra este proceso para
el caso del Cubo romo, que parte del Cuboctaedro Truncado (también llamado Gran Rombicuboctaedro)

30. FUENTES DE INFORMACIÓN:
http://www.sacred-
geometry.es/es/content/s%C3%B3li
dos-arquimedianos
https://www.uam.es/personal_pdi/ci
encias/barcelo/historia/Los%20solid
os%20platonicos.pdf
http://www.disfrutalasmatematicas.
com/geometria/solidos-
platonicos.html
http://www.portalplanetasedna.com
.ar/trece_solidos.htm