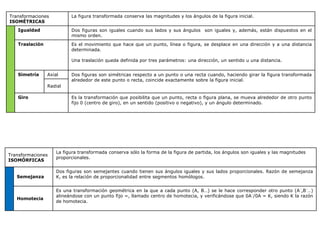
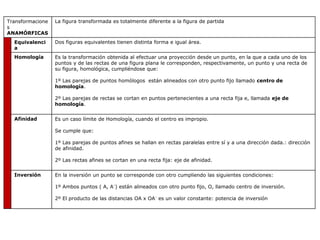
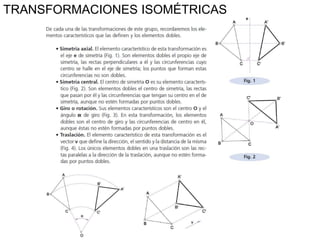
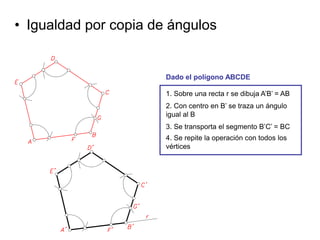
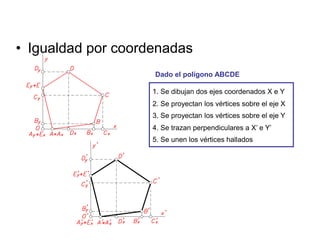
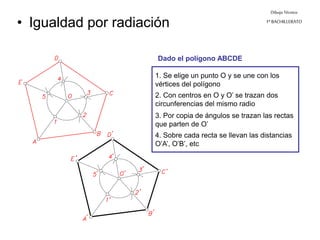
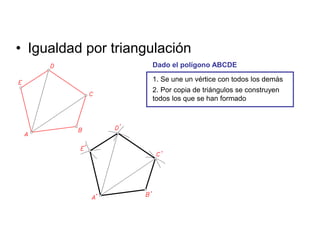
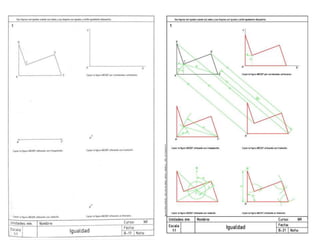
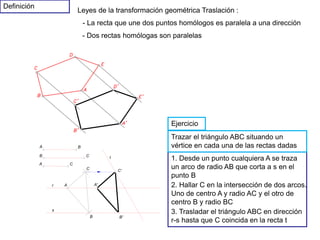
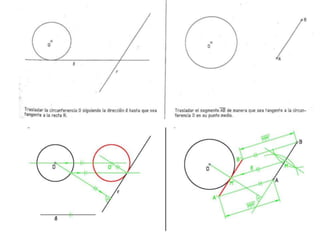
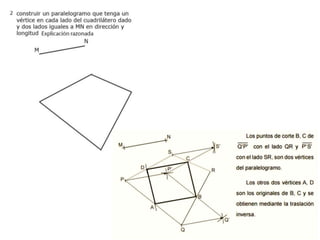
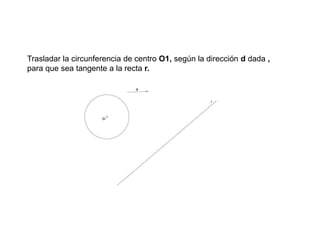
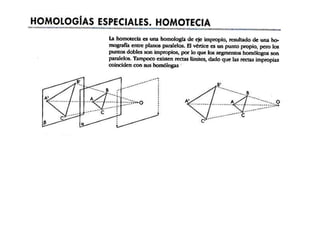
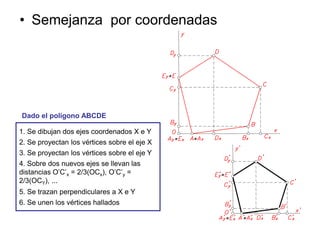
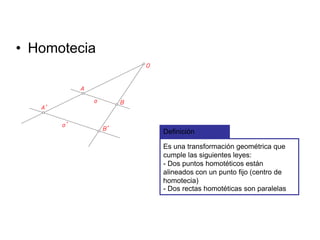
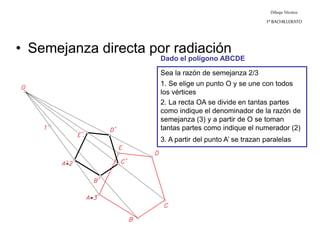
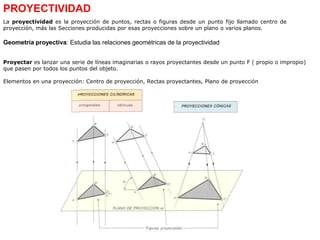
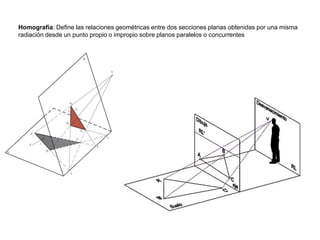
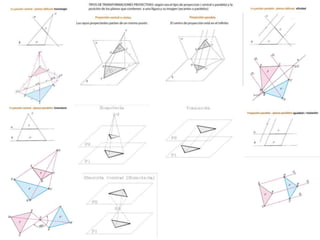
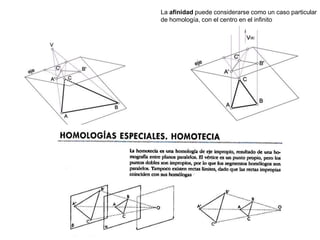
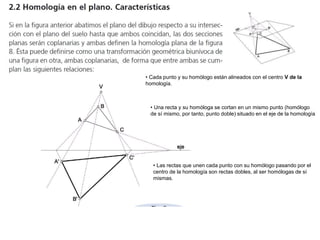
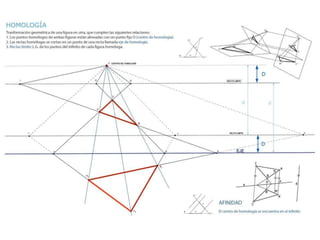
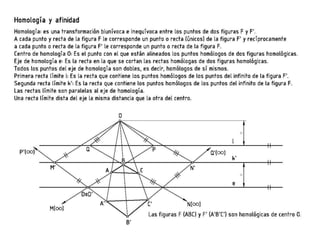
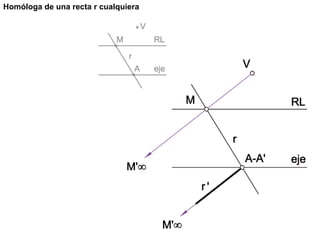
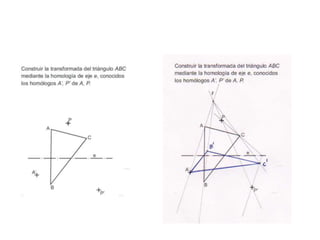
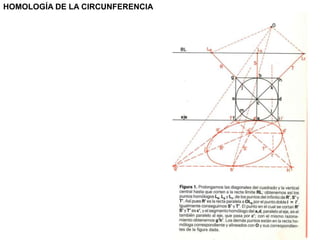
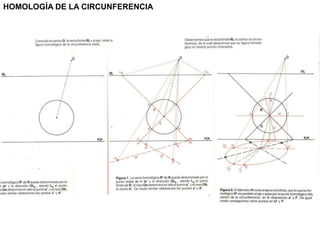
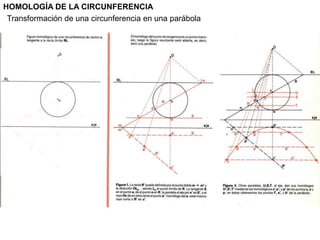
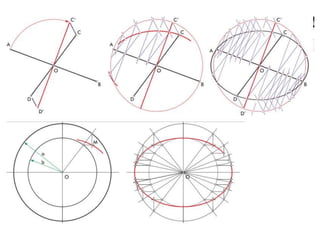
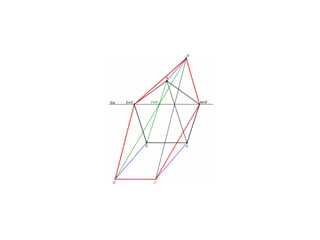
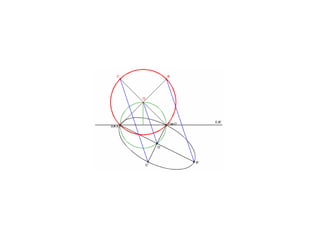
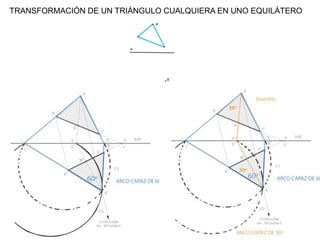
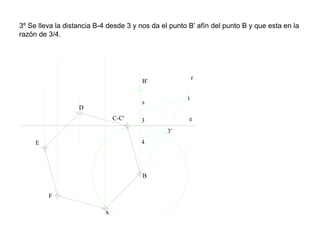
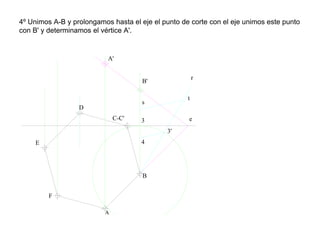
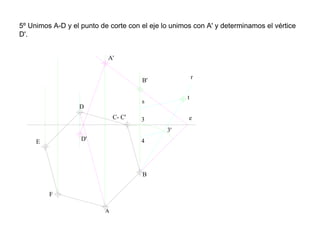
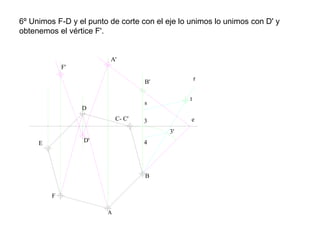
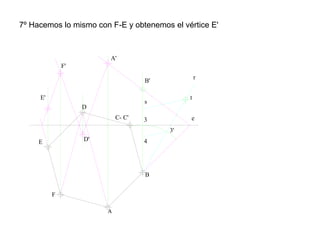
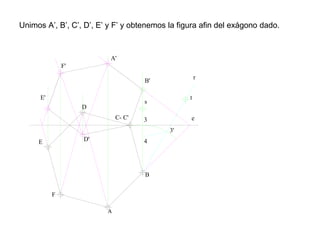
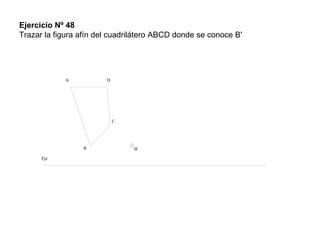
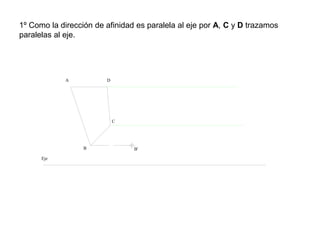
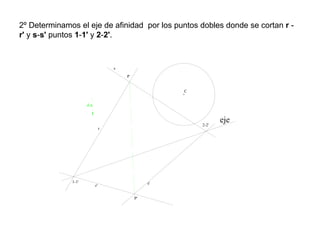
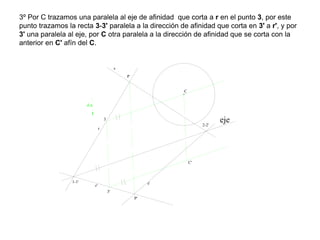
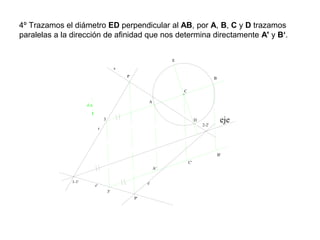
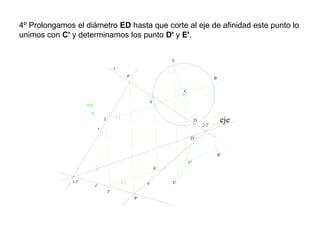
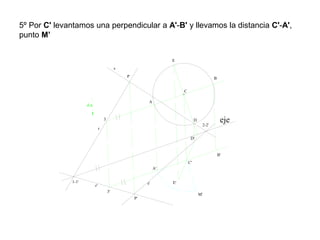
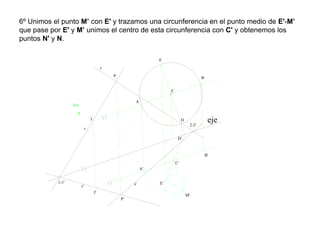
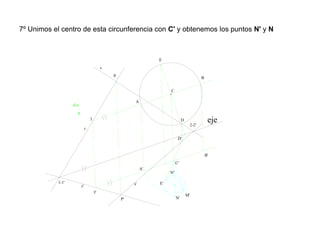
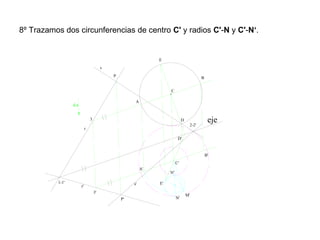
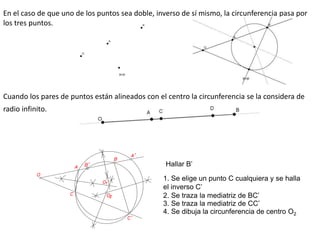
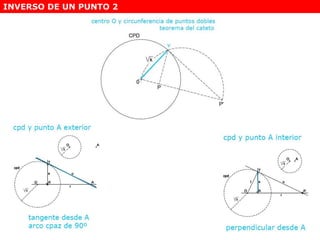
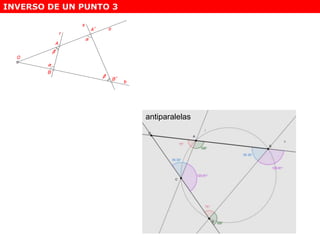
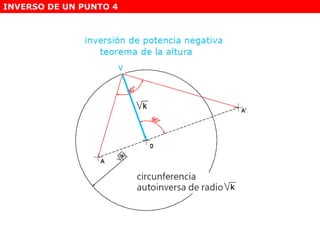
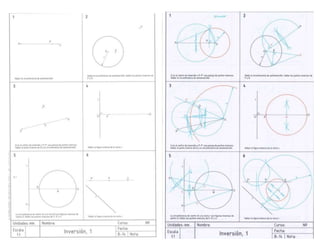
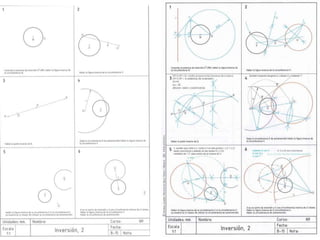
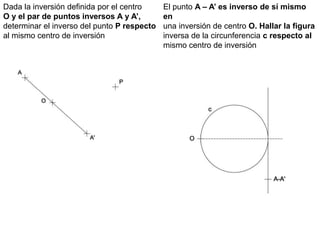
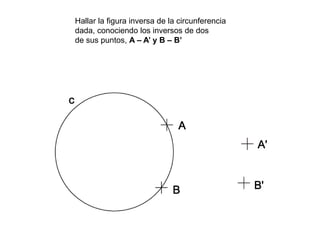
Este documento describe diferentes tipos de transformaciones geométricas. Define transformaciones isométricas como aquellas que conservan las magnitudes y ángulos de la figura original, e incluye la igualdad, traslación, simetría y giro como ejemplos. También describe transformaciones isomórficas como homotecias y semejanza que conservan solo la forma, y transformaciones anamórficas como equivalencia, homología, afinidad e inversión que cambian completamente la figura.