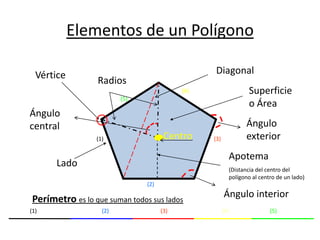
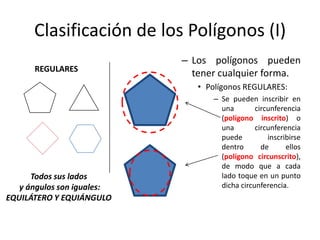
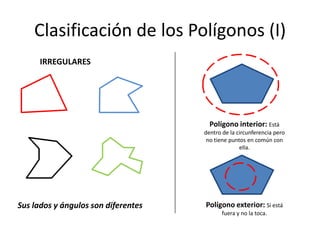
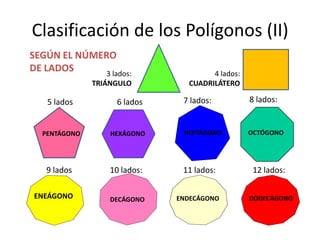
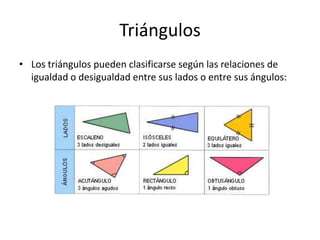
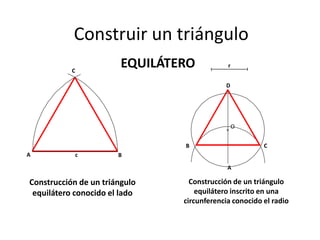
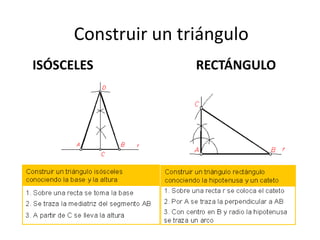
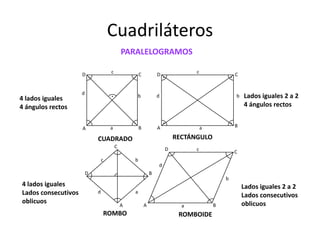
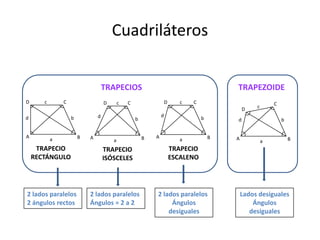
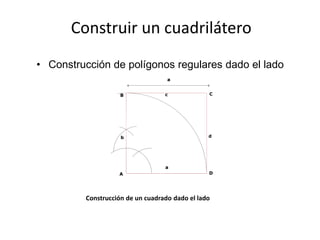
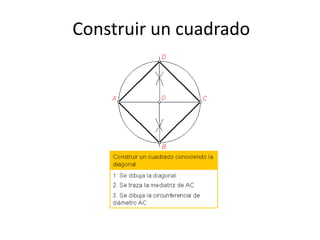
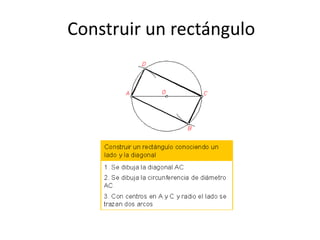
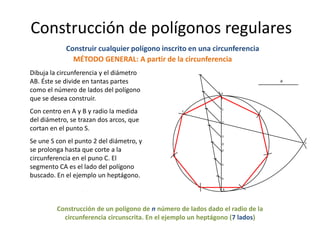
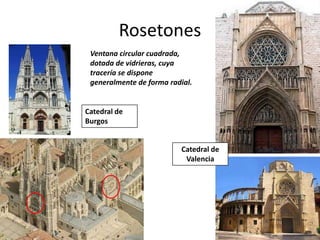
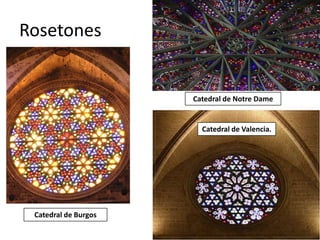
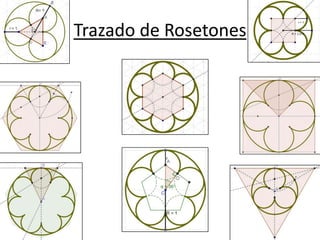
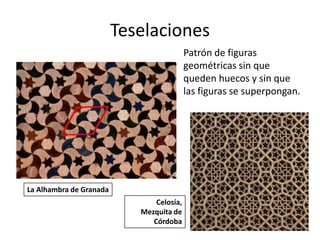
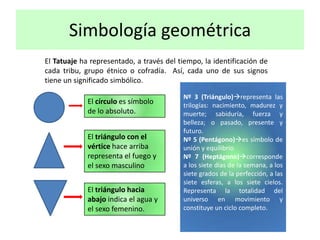
Este documento presenta información sobre las formas poligonales y estrelladas y su uso en el arte y la arquitectura. Explica los elementos básicos de los polígonos como lados, vértices y ángulos. Describe diferentes tipos de polígonos como triángulos, cuadriláteros y polígonos regulares e irregulares. Luego analiza el uso de estas formas geométricas en obras de artistas como Klee, Kandinsky, Picasso y Mondrian, así como en elementos arquitectónicos como rosetones, mosaicos y

1. Máster en Formación de Profesorado para ESO y Bachillerato.Módulo Específico:DIBUJOComplementos para la Formación Disciplinar del DibujoMATERIAL DIDÁCTICO31 de Mayo de 2011Profesor: Amador MéndezCelia López de MiguelGrupo -11

2. LA GEOMETRÍA EN EL ARTEFormas Poligonales y EstrelladasCurso 1º E.S.O.

3. TODOLOQUE NOSRODEAESTÁSOMETIDOAUNORDENGEOMÉTRICO,TANTOINTERNOCOMOEXTERNO.

4. Las Formas Poligonales en el EntornoIDÓNEOS PARA EXPRESAR ORDEN Y MEDIDADISEÑOS DECORATIVOSCOMUNICACIÓN VISUALPROYECTOS NATURALES

5. ¿Qué es un Polígono?Si tenemos un planoY en ese plano dibujamos una serie de segmentos, uno a continuación de otro (línea poligonal), de manera que la línea este cerrada.El trozo de plano que queda dentro de la línea es a lo que llamamos “POLÍGONO”

6. DEFINICIÓN de PolígonoEsunaporcióndeplanocerradaporlíneasrectasquesecortan.

7. Elementos de un PolígonoLos polígonos están compuestos por:Lados: son los diferentes segmentos de la línea quebrada.Vértices: son los puntos donde la línea poligonal cambia de dirección.Centro: punto interior que se encuentra a igual distancia de sus vértices.Radio del polígono: es el radio de la circunferencia circunscrita  es un segmento que une el centro con cualquier punto de la circunferencia.Apotema: perpendicular trazada desde el centro de un polígono regular hasta uno de sus lados.

8. Elementos de un PolígonoLos polígonos están compuestos por:Diagonal: recta que une dos vértices no consecutivos.Contorno: límite exterior de la figura.Perímetro: suma de la longitud de sus lados.Área: superficie interior del polígono.Ángulos:INTERIOR: los formados en el interior del polígono entre dos lados adyacentes.EXTERIOR: los formados en el exterior del polígono por un lado cualquiera y la prolongación de su lado adyacente.CENTRAL: el que forman dos apotemas o radios consecutivos.

9. Elementos de un PolígonoDiagonalVérticeRadiosSuperficie o Área(4)(5)ÁngulocentralÁngulo exteriorCentro(1)(3)Apotema(Distancia del centro del polígono al centro de un lado)Lado(2)Ángulo interiorPerímetroes lo que suman todos sus lados(1)(2)(3)(4)(5)

10. Clasificación de los Polígonos (I)Los polígonos pueden tener cualquier forma.Polígonos REGULARES:Se pueden inscribir en una circunferencia (polígono inscrito) o una circunferencia puede inscribirse dentro de ellos (polígono circunscrito), de modo que a cada lado toque en un punto dicha circunferencia.REGULARESTodos sus lados y ángulos son iguales:EQUILÁTERO Y EQUIÁNGULO

11. Clasificación de los Polígonos (I)IRREGULARESPolígono interior: Está dentro de la circunferencia pero no tiene puntos en común con ella.Sus lados y ángulos son diferentesPolígono exterior: Si está fuera y no la toca.

12. HEPTÁGONOOCTÓGONOENEÁGONODECÁGONOENDECÁGONODODECÁGONOClasificación de los Polígonos (II)8 lados:7 lados:SEGÚN EL NÚMERO DE LADOSHEPTÁGONOOCTÓGONO4 lados: CUADRILÁTERO3 lados: TRIÁNGULOENEÁGONO6 lados5 lados12 lados:11 lados:10 lados:HEXÁGONOPENTÁGONO9 ladosENDECÁGONODODECÁGONODECÁGONO

13. TriángulosDefinición:El triángulo es un polígono de tres lados y tres vértices. Los triángulos son los únicos polígonos que no tienen diagonales. Recuerda que en un triángulo rectángulo:Los dos lados perpendiculares se llaman catetos. El tercer lado, el más largo, se llama hipotenusa.

14. TriángulosLos triángulos pueden clasificarse según las relaciones de igualdad o desigualdad entre sus lados o entre sus ángulos:

15. DrOAcConstruir un triánguloEQUILÁTEROCCBABConstrucción de un triángulo equilátero conocido el ladoConstrucción de un triángulo equilátero inscrito en una circunferencia conocido el radio

16. Construir un triánguloISÓSCELESRECTÁNGULO

17. CuadriláterosEl cuadrilátero es un polígono de cuatro lados y cuatro vértices. Según las relaciones que se establecen entre sus lados y entre sus ángulos, pueden distinguirse tres tipos de cuadriláteros: paralelogramos, trapecios y trapezoides.

18. cDCbdBaACcDCbcdBDbadABAaDEFINICIÓN: Polígono de cuatro ladosPARALELOGRAMOScCDdLados iguales 2 a 24 ángulos rectos b4 lados iguales4 ángulos rectos BaARECTÁNGULOCUADRADO4 lados igualesLados consecutivos oblicuosLados iguales 2 a 2Lados consecutivos oblicuosROMBOROMBOIDECuadriláteros

19. cCDcCDdbdbABaABacCDCcdDbdbABaABaTRAPECIOSTRAPEZOIDETRAPECIO RECTÁNGULOTRAPECIO ESCALENOTRAPECIO ISÓSCELES2 lados paralelos2 ángulos rectos2 lados paralelosÁngulos = 2 a 22 lados paralelosÁngulos desigualesLados desigualesÁngulos desigualesCuadriláteros

20. Construir un cuadriláteroConstrucción de polígonos regulares dado el ladoConstrucción de un cuadrado dado el lado

21. Construir un cuadrado

22. Construir un rectángulo

23. a123456Construcción de polígonos regularesConstruir cualquier polígono inscrito en una circunferenciaMÉTODO GENERAL: A partir de la circunferenciaDibuja la circunferencia y el diámetro AB. Éste se divide en tantas partes como el número de lados del polígono que se desea construir.Con centro en A y B y radio la medida del diámetro, se trazan dos arcos, que cortan en el punto S.Se une S con el punto 2 del diámetro, y se prolonga hasta que corte a la circunferencia en el puno C. El segmento CA es el lado del polígono buscado. En el ejemplo un heptágono.ACSOBConstrucción de un polígono de n número de lados dado el radio de la circunferencia circunscrita. En el ejemplo un heptágono (7 lados)

24. Polígonos EstrelladosSe obtienen a partir de los polígonos regulares, pero cambiando el orden de unión de sus vértices; Es decir, haciéndolo de forma alternativa, no consecutiva. Los intervalos deben ser fijos.POLÍGONO ESTRELLADO DE CINCO PUNTASPOLÍGONO ESTRELLADO DE SEIS PUNTAS

25. 12837645Los polígonos estrellados tienen lados y ángulos iguales.POLÍGONO ESTRELLADO DE DIEZ PUNTASPOLÍGONO ESTRELLADO DE OCHO PUNTASPolígonos Estrellados

26. UsodeformaspoligonalesenelARTEVarias son las épocas y los campos artísticos que han utilizado las formas poligonales para expresarse.Vamos a conocer algunos por ejemplo: elementos propios de la decoración musulmana, el rosetón gótico o la abstracción geométrica.

27. GeometríaenlaPinturaPietMondrianPaul Klee…

28. Paul KleePuente rojo, 1928 Sinfonía de colores, 1928El jardín del templo, 1920Senecio, 1919Castillo y sol, 1928Flores en la arena, 1927Globo rojo, 1922.

29. “Cuando hoy miramos a nuestro alrededor, vemos toda suerte de formas exactas y homogéneas; nos guste o no, nuestros ojos engullen cuadrados, círculos, y todo tipo de formas fabricadas más o menos distintas en relaciones elaboradas…”Paul Klee.

30. Vasily KandinskyComposición VIII, 1923Línea transversal, 1923Amarillo, rojo y azul; 1925

31. KazimirMalévichPor la mañana, después de la tormenta, en la aldea; 1912Suprematismo, 1915Suprematismo, 1916-1917

32. Pablo PicassoHorta de Ebro, la fábrica; 1.909Retrato de WilhelmUhde, 1.910Casas en la colina (Hora de Ebro), 1.909El depósito de agua de Horta de Ebro, 1.909

33. Pablo Picasso y el CubismoMovimiento artístico que tuvo lugar en las dos primeras décadas del siglo XX.Picasso fue quien abrió paso a este movimiento artístico.El Cubismo muestra al mismo tiempo diferentes vistas de lo representado, utilizando para ello formas geométricas muy simples: triángulos, rectángulos, cuadrados…

34. PietMondrianComposición con Rojo, Amarillo y Azul, 1928Cuadro nº 1, 1921Cuadro nº 2, 1921-1925

35. Frank StellaFlinFlon VI, 1970HyenaStomp, 1962

36. GeometríaenlaArquitecturaMosaicos.Teselaciones.Lacerías.Rosetones.Cúpulas.

37. LaceríasOrnamentación geométrica que consiste en una serie de líneas entrecruzadas alternativamente unas sobre otras, formando diversas figuras estrelladas y poligonales.La Alhambra, GranadaMezquita de Córdoba

38. RosetonesVentana circular cuadrada, dotada de vidrieras, cuya tracería se dispone generalmente de forma radial.Catedral de BurgosCatedral de Valencia

39. RosetonesCatedral de Valencia.Catedral de Notre DameCatedral de Burgos

40. Trazado de Rosetones

41. TeselacionesPatrón de figuras geométricas sin que queden huecos y sin que las figuras se superpongan.La Alhambra de GranadaCelosía, Mezquita de Córdoba

42. CúpulasCúpula de laMaqsura,Mezquita de CórdobaCúpula estrellada del cimborrio de la Catedral de BurgosMihrab de la Mezquita de Córdoba

43. Mezquitade la Roca,JerusalénEdificiosPirámide de cristal del Museo Louvre, París

44. GeometríaenotrasartesTatuajes permanentes.Tatuajes temporales.Henna.Simbolismo:CuadradoCírculoTriángulo

45. Simbología geométricaEl Tatuaje ha representado, a través del tiempo, la identificación de cada tribu, grupo étnico o cofradía. Así, cada uno de sus signos tiene un significado simbólico. Nº 3 (Triángulo)representa las trilogías: nacimiento, madurez y muerte; sabiduría, fuerza y belleza; o pasado, presente y futuro. Nº 5 (Pentágono)es símbolo de unión y equilibrioNº 7 (Heptágono)corresponde a los siete días de la semana, a los siete grados de la perfección, a las siete esferas, a los siete cielos. Representa la totalidad del universo en movimiento y constituye un ciclo completo. El círculo es símbolo de lo absoluto.El triángulo con el vértice hace arriba representa el fuego y el sexo masculinoEl triángulo hacia abajo indica el agua y el sexo femenino.

46. Tatuajes

47. Henna

48. ConclusionesLas formas geométricas pueden resultar tan artísticas como cualquiera, aunque también tengan un carácter técnico.Los trazos dentro de estas obras no están hechos aleatoriamente, sino que son razonados.

49. ActividadesHacer una composición personal a la manera de uno de los pintores presentados.Reinterpretar un cuadro haciendo uso de formas poligonales.Autorretrátate usando para ellos los polígonos que ya conoces.

50. PUEDES COMPLETAR O AMPLIAR LOS CONTENIDOS EN ESTAS DIRECCIONES:http://www.educacionplastica.nethttp://www.educacionplastica.net/MenuTrazados.htmhttp://www.educacionplastica.net/PolEst0.htm (polígonos y polígonos estrellados)http://www.xtec.es/~epuig124/mates/geometria/castella/index.htm (unidad didáctica de geometría)http://ntic.educacion.es/w3//eos/MaterialesEducativos/mem2001/dibujotecnico/Construcciones%20de%20dibujo%20tecnico/entrd.htm (construcciones de dibujo técnico y actividades)http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=10298:4-octubre-2009-geometren-rosetones-gos&catid=198:geometrdinca-y-matemcas-interactivas&directory=67 (geometría en rosetones góticos)http://educacionplastica.net/poligonos.htm (construcción de polígonos regulares)http://roble.pntic.mec.es/jarran2/cabriweb/Poligonos.htm (polígonos y webs sobre el tema)http://pintura.aut.org/ (artistas y obras)