El documento describe la solución de la ecuación de Schrödinger para una partícula en un pozo de potencial cuadrado de paredes infinitas. Se resuelve primero para un solo grado de libertad y luego se generaliza para dos grados de libertad. La solución implica funciones propias discretas que dependen de números cuánticos enteros y conducen a valores propios discretos de energía.

1. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
POZO POTENCIAL DE PAREDES
INFINITAS
G. Muños, F. Medina, H. Galindo
Universidad Pedagógica y Tecnológica de Colombia
17 de Octubre de 2012

2. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
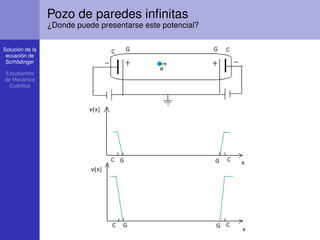
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
Potencial
Se considera una partícula libre con un grado de libertad
translacional
V(x) =
0 = x [−a, a]
∞ = x¡[−a, a]

3. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
¿Donde puede presentarse este potencial?

4. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
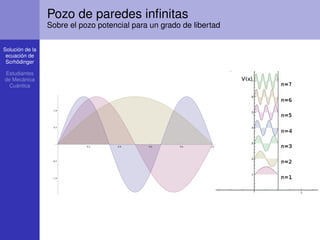
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
Debido a la discontinuidad del potencial la ecuación de
Scrödinger debe ser resuelta en I, II, III x < −a,
−a ≤ x ≤ a y x > a.
El potencial es nulo en la región II, la solución es de la
forma
ψII(x) = A exp[ikx] + B exp[−ikx] (1)
Para el caso de las regiones I y III se tiene que
ψI(x) = 0 ∧ ψIII(x) = 0
Por continuidad de la función de onda en x = −a y
x = a la solución para la región II debe satisfacer las
condicione de frontera
ψII(−a) = ψI(−a) = 0 ∧ ψII(a) = ψIII(a) = 0 (2)

5. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
Evaluando (1) en los puntos de −a y a y aplicando las
condiciones planteadas en (2) tenemos
ψII(−a) = A exp [−ika] + B exp [ika] = 0
ψII(a) = A exp [ika] + B exp [−ika] = 0
Sumando las dos ecuaciones se tiene
A
@@@@@@@@@@@@
(exp [−ika] + exp [ika]) = −B
@@@@@@@@@@@@
(exp [ika] + exp [−ika])
A = −B
Así entonces la ecuación de onda queda
ψII(x) = A {exp [ikx] − exp [−ikx]} = A sin (kx)

6. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
De las condiciones se tiene que sin (ka) = 0 lo que nos dice
que ka = nπ donde n = 1, 2, 3... notemos que n = 0 no es
una solución cuántica ya que para este valor k sería nulo,
de lo contrario se estaría contradiciendo el hecho de que
todo posible estado cuántico debe estar representado por
una función de onda cuya norma sea nula.
Así tenemos que como
k =
√
2mE
nπ
a =
√
2mE
En =
2π2
2ma2 n2
En = εn2 n = 1, 2, ...

7. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
Ya encontrado k las funciones propias asociadas a cada
valor propio serán
ψn(x) = A sin
nπ
a
x , n = 1, 2, 3, ...
Donde n se le llama número cuántico principal y se utiliza
para caracterizar los valores propios de energía.
´ ∞
−∞ dx|ψn(x)|2
Para encontrar la constante de normalización se hace
|A’|2
ˆ a
−a
dx sin2 nπx
a
= |A |2
= 1

8. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
⇒ ψ(x) = sin
nπ
a
x n = 1, 2, 3, ...
n = 3 ψ3(x) = sin
3π
a
x
n = 2 ψ2(x) = sin
2π
a
x
n = 1 ψ1(x) = sin
π
a
x estado base

9. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
⇒ ψ(x) = sin
nπ
a
x n = 1, 2, 3, ...
n = 3 ψ3(x) = sin
3π
a
x
n = 2 ψ2(x) = sin
2π
a
x
n = 1 ψ1(x) = sin
π
a
x estado base

10. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Sobre el pozo potencial para un grado de libertad
0.2 0.4 0.6 0.8 1.0
1.0
0.5
0.5
1.0

11. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Comparación con el modelo clásico

12. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Comparación con el modelo clásico
Tenemos un potencial para la partícula V(x) así su fuerza
es
F =
dV
dx
a =
d2x
dt2
x = x(t) v =
dx
dt
La probabilidad clásica de encontrar la partícula Pc(x) = 1
a

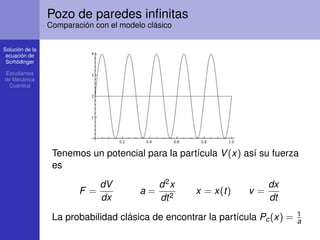
13. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Potencial
Se considera una partícula con dos grados de libertad
translacionales en el campo de fuerzas definido por el
potencial
V(x1, x2) =
0 Para x1 [0, a] , x2 [0, a]
∞ para x1¡ [0, a] , x2¡ [0, a]
La ecuación de Schrödinger independiente del tiempo
bidimensional es
−
2
2m
∂2
x1
−
2
2m
∂2
x2
ψ(x1, x2) = Eψ(x1, x2)
x [0, a] , x2 [0, a]

14. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Condiciones de frontera
ψ (x1, x2) |x1=0,x2=0= 0, ψ (x1, x2) |x1=a,x2=a= 0
Se propone una solución de la forma
ψ(x1, x2) = ϕ1 (x1) ϕ2 (x2) para obtener
−
2
2m
∂2
x1
ϕ1 (x1) = αϕ1 (x1) ⇒ ∂2
x1
+ k2
1 ϕ1 (x1) = 0
−
2
2m
∂2
x2
ϕ2 (x2) = βϕ2 (x2) ⇒ ∂2
x2
+ k2
2 ϕ2 (x2) = 0
donde α es la constante de separación de las variables
β = (E − α), k1 =
√
2mα
y k2 =
√
2mβ

15. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Las soluciones de cada una de las ecuaciones se pueden
expresar
ψ1(x1) = A1 exp[ik1x1] + A2 exp[−ik1x1]
ψ2(x2) = B1 exp[ik2x2] + B2 exp[−ik2x2]
Aplicando las condiciones de frontera para el primer grado
de libertad se obtiene
ϕ1 (x1) |x1=0= 0 → A1 = A2 ⇒ ϕ1 (x1) = A sin (k1x1)
ϕ1 (x1) |x1=a= 0 → k1 = πn1
a ⇒ ϕn1
(x1) = A sin n1πx1
a
Donde n1 = 1, 2, 3...

16. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Para el segundo grado de libertad se tiene
k2 =
n2π
a
, ϕn2
(x2) = B sin
n2πx2
a
, n2 = 1, 2, 3, ...
Como los valores de k1 y k2 están restringidos a múltiplos
enteros de π
a . La desretización de los números de onda
conducen a la discretización de los valores de las constates
α y β
αn1
=
2π2
2ma2
n2
1 = ε1n2
1, βn2
=
2π2
2ma2
n2
2 = ε2n2
2
Como β = (E − α), se obtienen los siguientes valores
propios de energía
En1,n2
= ε1n2
1 + ε2n2
2

17. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Las correspondientes funciones propias son
ψn1,n2
(x1, x2) = ϕn1
(x1) ϕn2
(x2)
= N sin
n1πx1
a
sin
n2πx2
a
´
dx1dx2ψ∗
n1,n2
(x1, x2) ψn1,n2
(x1, x2) = 1
|N|2
ˆ
dx1 sin2 n1πx1
a
ˆ
dx2 sin2 n2πx2
a
= |N|2 a2
4
Las funciones propias normalizadas son
ψn1,n2
(x1, x2) =
2
a
sin
n1πx1
a
sin
n2πx2
a

18. Solución de la
ecuación de
Scrhödinger
Estudiantes
de Mecánica
Cuántica
Pozo de paredes infinitas
Generalización a dos grados de libertad
Valor propio degeneramiento funciones propias
E1 = 2ε no degenerado ψ1,1
E2 = 2ε 2 ψ1,2, ψ2,1
E3 = 2ε no degenerado ψ2,2
E4 = 2ε 2 ψ1,3, ψ3,1
E4 = 2ε 2 ψ2,3, ψ3,2
E5 = 2ε 2 ψ1,4, ψ4,1
E6 = 2ε no degenerado ψ3,3