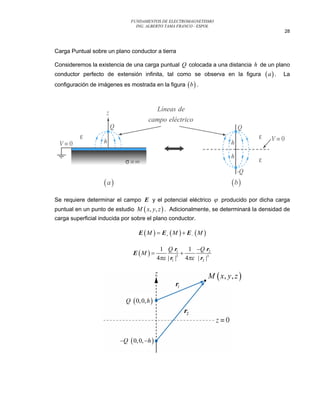
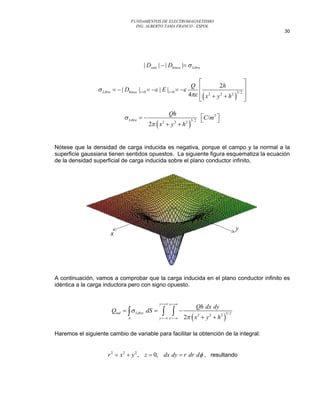
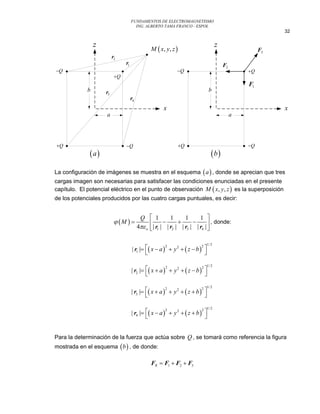
Este documento describe el método de las imágenes para resolver problemas electrostáticos. Este método reemplaza cargas reales por cargas reales e imágenes para satisfacer las condiciones de frontera en conductores. Se explica cómo determinar el potencial eléctrico, campo eléctrico y densidad de carga inducida para una carga puntual sobre un plano conductor. También se muestra cómo aplicar el método a una carga entre dos planos conductores para determinar el potencial y la fuerza sobre la carga.

1. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
27
MÉTODO DE LAS IMÁGENES
Ideado por Lord Kelvin en 1848. El método de imágenes, es de uso frecuente para deter-
minar  , E , D y  debidos a cargas en presencia de conductores. Este método
prescinde de la ecuación de Poisson o Laplace, pues se fundamenta en el supuesto de
una superficie conductora equipotencial. Aunque no es aplicable a cualquier problema
electrostático, puede simplificar problemas muy complejos.
La teoría de las imágenes establece que una configuración de carga dada sobre un plano
conductor perfecto e infinito conectado a tierra puede reemplazarse por la propia
configuración de carga, su imagen y una superficie equipotencial en sustitución del plano
conductor.
En la figura (a), se muestran ejemplos comunes de distribuciones de carga puntual, lineal y
volumétrica, mientras que en la figura (b), aparecen sus correspondientes configuraciones
de imagen.
Q   Q  
Q 

a b
La aplicación del método de imágenes, exige invariablemente el cumplimiento de dos
condiciones:
1. La carga o cargas de imágenes deben situarse en la región conductora.
2. La carga o cargas de imágenes deben situarse de tal forma que en la superficie o
superficies conductoras el potencial sea de cero o constante.
La primera condición es necesaria para satisfacer la ecuación de Poisson, en tanto que la
segunda garantiza la satisfacción de las condiciones en la frontera.
Apliquemos la teoría de las imágenes al caso de una carga puntual sobre un plano
conductor a tierra.
En la siguiente figura se esquematizan las líneas de campo para la carga original y para el
conjunto de carga original + carga imagen. Las líneas de campo son perpendiculares a la
superficie límite donde se induce una carga.

2. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
28
Carga Puntual sobre un plano conductor a tierra
Consideremos la existencia de una carga puntual Q colocada a una distancia h de un plano
conductor perfecto de extensión infinita, tal como se observa en la figura a . La
configuración de imágenes es mostrada en la figura  b  .
Líneas de
campo eléctrico
h h
h
a b
Se requiere determinar el campo E y el potencial eléctrico  producido por dicha carga
puntual en un punto de estudio M  x, y, z  . Adicionalmente, se determinará la densidad de
carga superficial inducida por sobre el plano conductor.
E  M   E  M   E  M 
1 Q r1 1 Q r2
E M   
4 | r1 | 4 | r2 |3
3
M x, y , z
r1
Q  0, 0, h 
r2
Q  0, 0, h 

3. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
29
Donde los vectores r1 y r2 están dados por:
r1   x, y, z    0, 0, h    x, y, z  h   x x  y  y   z  h   z
r2   x, y, z    0, 0, h    x, y, z  h   x  x  y  y   z  h   z
 
Q  x x  y  y   z  h   z x x  y  y   z  h  z 
E M     
4   x 2  y 2   z  h 2  3/ 2  x 2  y 2   z  h 2  3/ 2 
     
Nótese el hecho de que cuando z  0 , E  M  solo cuenta con la componente z , lo que
confirma que el campo eléctrico es normal a la superficie conductora, tal como se aprecia en
la siguiente figura.
A continuación pasaremos a determinar el potencial aplicando nuevamente el principio de
superposición, es decir:
Q Q
  M     M     M   
4 | r1 | 4 | r2 |
 
Q  1 1  , donde   x, y, z   0 si z  0
 M   
4  x2  y 2   z  h 
2
x2  y 2   z  h 
2 
 
Para obtener la densidad de carga inducida en el
plano conductor infinito, dicha densidad puede ser
determinada por aplicación del Teorema de Gauss
a un cilindro recto de altura muy pequeña y bases
paralelas a la frontera, una a cada lado, tal como se
muestra en la siguiente figura. Alternativamente,
también puede ser determinada mediante la
segunda condición de frontera.

4. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
30
| Dsale |  | Dhinca |  Libre
 
Q  2h 
 Libre   | Dhinca |z 0   | E |z 0  
4   x 2  y 2  h 2 3/ 2 
 
Qh
 Libre    C /m 2 
 
2  x  y  h
2 2

2 3/ 2
Nótese que la densidad de carga inducida es negativa, porque el campo y la normal a la
superficie gaussiana tienen sentidos opuestos. La siguiente figura esquematiza la ecuación
de la densidad superficial de carga inducida sobre el plano conductor infinito,
A continuación, vamos a comprobar que la carga inducida en el plano conductor infinito es
idéntica a la carga inductora pero con signo opuesto.
y  x 
Qh dx dy
Qind    Libre dS    
2  x 2  y 2  h 2 
3/ 2
A y  x 
Haremos el siguiente cambio de variable para facilitar la obtención de la integral:
r 2  x 2  y 2 , z  0, dx dy  r dr d , resultando

5. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
31
y  2 r  r  r 
Qh r dr d Qh r dr r dr
Qind      2    Qh 
2 r 
2 3/ 2 2 r 
2 3/ 2
r  h2 
3/ 2
 0 r 0
2
h r 0
2
h r 0
2
Qh r 
Qind  | r 0
 Q  l.q.q.d .
r 2  h2
2.4 Una carga puntual Q se localiza en el punto  a, 0, b  entre dos planos conductores
semiinfinitos que intersecan en ángulo recto, tal como se muestra en la figura. Determine el
potencial eléctrico producido en el punto M  x, y, z  y la fuerza que actúa sobre Q .
z
a Q
b
x
Los diagramas correspondientes para la determinación del potencial eléctrico y la fuerza
eléctrica, se aprecian en los esquemas  a  y  b  siguientes.

6. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
32
z z
M  x, y , z  F3
r2
r1 F2
Q Q Q
Q
F1
b r3 b
r4
x x
a a
Q Q Q Q
a b
La configuración de imágenes se muestra en el esquema  a  , donde se aprecian que tres
cargas imagen son necesarias para satisfacer las condiciones enunciadas en el presente
capítulo. El potencial eléctrico en el punto de observación M  x, y, z  es la superposición
de los potenciales producidos por las cuatro cargas puntuales, es decir:
Q  1 1 1 1 
 M        , donde:
4 o  | r1 | | r2 | | r3 | | r4 | 
1/ 2
| r1 |  x  a   y 2   z  b  
2 2
 
1/ 2
| r2 |  x  a   y 2   z  b  
2 2
 
1/ 2
| r3 |  x  a   y 2   z  b  
2 2
 
1/ 2
| r4 |  x  a   y 2   z  b  
2 2
 
Para la determinación de la fuerza que actúa sobre Q , se tomará como referencia la figura
mostrada en el esquema  b  , de donde:
FR  F1  F2  F3

7. FUNDAMENTOS DE ELECTROMAGNETISMO
ING. ALBERTO TAMA FRANCO - ESPOL
33
Q2 Q2 Q2
FR   z     x    2ax  2bz 
4 o  2b  4 o  2a 
2 2 3/ 2
4 o  2a    2b  
2 2
 
Q2 Q2 Q2
FR   z    x    2ax  2bz 
16 ob 2 16 o a 2 32 o  a 2  b 2 
3/ 2
 
 
Q2  1 1 a b
FR   2 z  2 x  x  z 
16 o  b  a 2  b2   a 2  b2  
3/ 2 3/ 2
a
 
     
Q2   a 1  b 1 
FR    2 x   2 z 
16 o    a 2  b 2  3/ 2
a    a 2  b2 3/ 2
b  
     
Se deja como ejercicio para el lector, la obtención de la intensidad de campo eléctrico
producido en el punto de observación M  x, y, z  , así como también la determinación de la
carga inducida en los planos conductores.
En general, cuando la metodología de las imágenes se aplica a un sistema consistente en
una carga puntual entre dos planos conductores semiinfinitos inclinados en un ángulo  ,
medido en grados, el número de imágenes N está dado por:
Q
 360o 
N   1
Q Q   
  60o
En la gráfica anexa, se muestra una carga
puntual Q contenida entre dos paredes
conductoras semiinfinitas e inclinadas entre
sí en un ángulo   60o . Se aprecia que el
Q Q número de cargas imagen son cinco.
Q