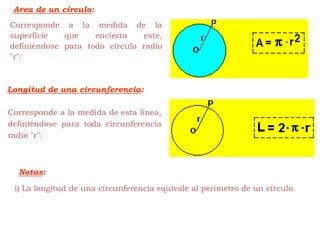
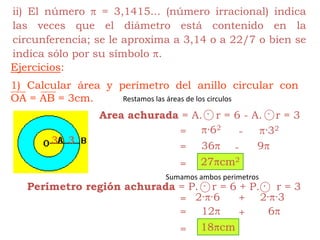
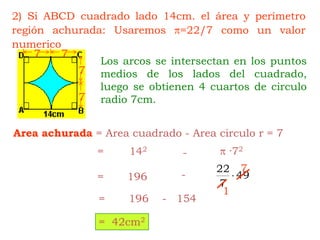
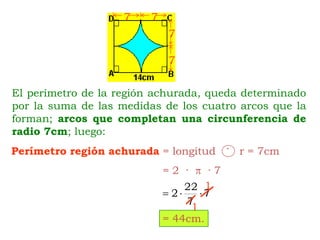
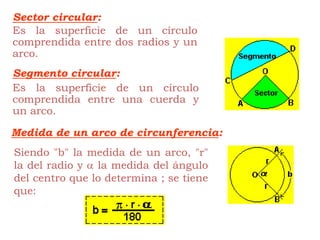
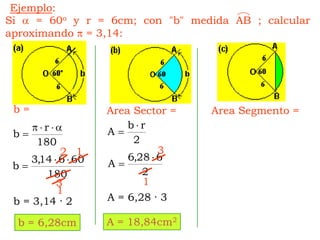
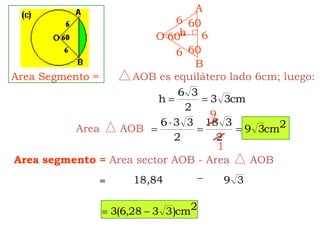
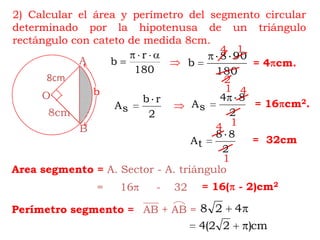
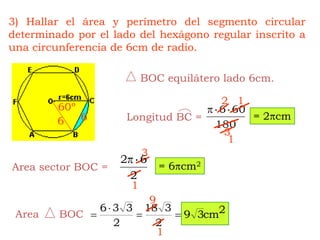
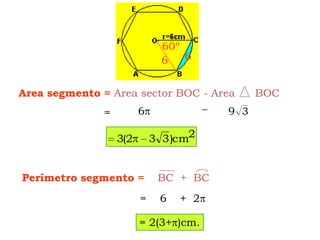
Este documento explica cómo calcular el área y perímetro de círculos, sectores circulares, segmentos circulares y áreas achuradas. Define las fórmulas para calcular el área de un círculo, sector y segmento circular, así como la longitud de una circunferencia. Proporciona ejemplos numéricos para ilustrar cómo aplicar estas fórmulas.

1. Area de un círculo:Corresponde a la medida de la superficie que encierra este, definiéndose para todo círculo radio "r":Longitud de una circunferencia:Corresponde a la medida de esta línea, definiéndose para toda circunferencia radio "r":Notas:i) La longitud de una circunferencia equivale al perímetro de un círculo.

2. Area achurada = A. r = 6 - A. r = 31) Calcular área y perímetro del anillo circular con OA = AB = 3cm. Perímetro región achurada = P. r = 6 + P. r = 3····ii) El número  = 3,1415... (número irracional) indica las veces que el diámetro está contenido en la circunferencia; se le aproxima a 3,14 o a 22/7 o bien se indica sólo por su símbolo .Ejercicios:Restamos las áreas de los circulos·62·32=-33369=-27cm2=Sumamos ambos perimetros2··62··3+=126=+18cm=

3. 77772) Si ABCD cuadrado lado 14cm. el área y perímetro región achurada: Usaremos =22/7 como un valor numericoLos arcos se intersectan en los puntos medios de los lados del cuadrado, luego se obtienen 4 cuartos de circulo radio 7cm.Area achurada= Area cuadrado - Area circulo r = 7 ·72=142-7-=1961= 196 - 154= 42cm2

4. 7777.Perímetro región achurada= longitud r = 7cmEl perímetro de la región achurada, queda determinado por la suma de las medidas de los cuatro arcos que la forman; arcos que completan una circunferencia de radio 7cm; luego:= 2 ·  · 711= 44cm.

5. Sector circular:Es la superficie de un círculo comprendida entre dos radios y un arco.Segmento circular:Es la superficie de un círculo comprendida entre una cuerda y un arco.Medida de un arco de circunferencia:Siendo "b" la medida de un arco, "r" la del radio y  la medida del ángulo del centro que lo determina ; se tiene que:

6. Area de un sector circular:Siendo "b" la medida del arco y "r" la del radio que lo determina, el área del sector circular queda determinada por:Area de un segmento circular:queda determinada por la diferencia entre el área del sector circular y el triángulo determinado por los radios que determinan el sector.

7. Ejemplo:Si  = 60o y r = 6cm; con "b" medida AB ; calcular aproximando  = 3,14:b =Area Sector =Area Segmento = 312131A = 6,28 · 3b = 3,14 · 2A = 18,84cm2b = 6,28cm

8. AOB es equilátero lado 6cm; luego:A6Area AOBhO60º6Area segmento =Area sector AOB - Area AOBB60660Area Segmento = 91_18,84=

9. Ejercicios:bAB72ºObCDOA + AB + BO + OD + DC + CO1) Determine el área y perímetro de la siguiente región determinada por dos diámetros de 20cm y que forman un ángulo de 72º.diámetro = 20cm radio = 10cmLongitud arco:4= 4cm.10101Area sector :10105= 20cm2.1Area achurada == 40cm22·Area sector= 2 ·20cm2Perímetro región ach. == 10 + 4 + 10 + 10 + 4 + 10= 40 + 8= 8(5 + )cm

10. A8cmbOBAB + AB =2) Calcular el área y perímetro del segmento circular determinado por la hipotenusa de un triángulo rectángulo con cateto de medida 8cm.14= 4cm.214= 16cm2.8cm14= 32cm1Area segmento =A. Sector - A. triángulo= 16( - 2)cm2= 16 - 32Perímetro segmento =

11. BOC equilátero lado 6cm.Longitud BC =Area BOC3) Hallar el área y perímetro del segmento circular determinado por el lado del hexágono regular inscrito a una circunferencia de 6cm de radio.1260º= 2cm66313= 6cm2Area sector BOC =191

12. 60º66Area segmento =Area sector BOC - Area BOCPerímetro segmento =BC + BC_6== 6 + 2= 2(3+)cm.

13. Nota Final: En general para calcular el área de la intersección de dos figuras (el área achurada) quedará determinada por la diferencia de las dos áreas, por otro lado el perímetro de estas quedara determinado dependiendo el contorno de la figura.