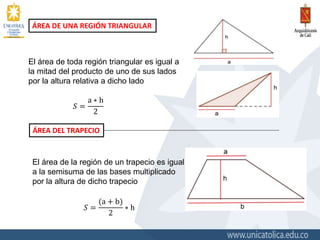
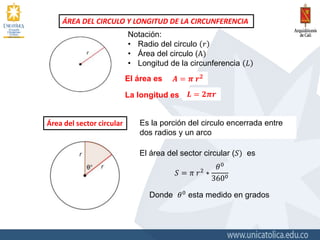
El documento explica fórmulas para calcular el área de diferentes figuras geométricas como rectángulos, triángulos, trapecios, círculos y sectores circulares. Proporciona ejemplos numéricos para ilustrar el cálculo del área de estas figuras usando las fórmulas correspondientes.

1. ÁREAS DE REGIONES
Área de una región rectangular
S = a ∗ b
Calcular el área de la región sombreada.Ejemplo 1
La región, se puede dividir en dos
rectángulos
• Primer rectángulo de lados 7 y 14
(14 = 24 - 10)
• Segundo rectángulo de lados 10 y 20
𝑆 = 7 ∗ 14 + (10 ∗ 20)
𝑆 = 98 + 200
𝑆 = 298
El área de la región es

2. ÁREA DE UNA REGIÓN TRIANGULAR
El área de toda región triangular es igual a
la mitad del producto de uno de sus lados
por la altura relativa a dicho lado
𝑆 =
a ∗ h
2
ÁREA DEL TRAPECIO
El área de la región de un trapecio es igual
a la semisuma de las bases multiplicado
por la altura de dicho trapecio
𝑆 =
(a + b)
2
∗ h

3. Si el cuadrado tiene perímetro 8 cm, hallar
el área de la región sombreada
Ejemplo 2
Si el perímetro del cuadrado
es 8 cm,
𝑃 = 𝑙 + 𝑙 + 𝑙 + 𝑙
12 = 4𝑙
12
4
= 𝑙
𝒍 = 𝟑 𝒄𝒎
El área del triángulo no sombreado (𝑇) es
𝑇 =
3 ∗ 3
2
𝑻 = 𝟒, 𝟓 𝒄𝒎 𝟐
El área de la región sombreada (𝑆) es
Notación para el cuadrado
• Área del cuadrado (𝐶)
• Perímetro del cuadrado (𝑃)
• Lado del cuadrado (𝑙)
cada lado del cuadrado
mide 3 cm
𝑆 = 𝐶 − 𝑇
𝑆 = (3 ∗ 3) − 4.5
𝑆 = 9 − 4.5
𝑺 = 𝟒. 𝟓 𝒄𝒎 𝟐

4. Notación:
• Radio del circulo 𝑟
• Área del circulo (A)
• Longitud de la circunferencia 𝐿
𝑨 = 𝝅 𝒓 𝟐
ÁREA DEL CIRCULO Y LONGITUD DE LA CIRCUNFERENCIA
El área es
Área del sector circular Es la porción del circulo encerrada entre
dos radios y un arco
El área del sector circular (𝑆) es
Donde 𝜃0 esta medido en grados
La longitud es 𝑳 = 𝟐𝝅𝒓
𝑆 = 𝜋 𝑟2
∗
𝜃0
3600

5. Dada una circunferencia de radio 1 m, calcular:
• La longitud de la circunferencia
• El área del sector circular de una
circunferencia de radio 1 metro y ángulo 300
Ejemplo 3
Utilizamos la fórmula para los ángulos en grados
𝑆 = 𝜋 𝑟2 ∗
𝜃0
3600
Sustituimos los datos: 𝑆 = 𝜋 12 ∗
300
3600
𝑆 =
𝜋
12
El área del sector circular es
𝝅
𝟏𝟐
𝒎 𝟐
Longitud circunferencia
𝑳 = 𝟐𝝅𝒓Utilizamos la fórmula
Sustituimos 𝒓 = 𝟏 entonces 𝑳 = 𝟐𝝅𝟏
𝟐𝛑 𝒎La longitud de la circunferencia es
Sector circular

6. Ejemplo 4 Calcular en grados el ángulo del sector circular con
área igual a 6𝜋 𝑐𝑚2
de un circulo donde la longitud de
la circunferencia es 4 2𝜋 𝑐𝑚.
Calculamos el radio de la circunferencia a partir
de su longitud (𝐿 = 2𝜋𝑟):
2𝜋𝑟 = 4 2𝜋
𝑟 =
4 2𝜋
2𝜋
𝑟 = 2 2 𝑐𝑚
Calculamos el ángulo expresado en grados a partir de la fórmula del
área de un sector circular
𝑆 = 𝜋 𝑟2
∗
𝜃0
3600
Sustituimos los datos
𝜋 2 2
2
∗
𝜃0
3600 = 6𝜋
𝜃0
=
6𝜋 ∗ 3600
𝜋 ∗ 2 2
2
𝜃0
=
6 ∗ 3600
8
𝜃0
=
6 ∗ 3600
8
𝜽 𝟎
= 𝟐𝟕𝟎 𝟎