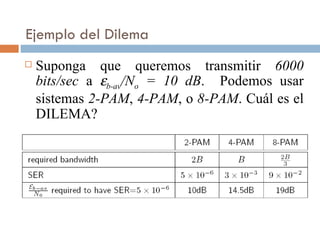
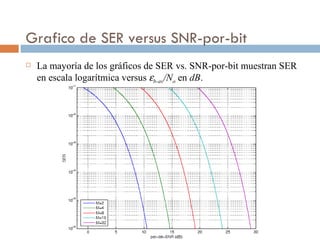
Este documento discute la probabilidad de error de símbolo (SER) en sistemas M-PAM. Explica que la SER aumenta con M, pero el ancho de banda requerido disminuye logarítmicamente con M. Esto crea un dilema entre eficiencia espectral y SER. También cubre cómo asignar bits a símbolos para minimizar errores comunes de un solo bit.

1. PROBABILIDAD DE ERROR DE SÍMBOLO M-PAM Dr. Boris Ramos

2. Probabilidad de Error de Símbolo M-PAM Para un sistema de comunicaciones 4-PAM, la probabilidad de una decisión de símbolo errada puede ser expresada como: Se puede demostrar que para un sistema M-PAM, la probabilidad de error de símbolo viene dada por:

3. Consideraciones Generales La cantidad  b-av /N o es conocida como la relación Señal a Ruido por bit (SNR-por-bit). Esta es la mejor forma de comparar los requerimientos de energía de 2 sistemas de comunicaciones. La probabilidad de error de símbolo es comúnmente conocida como la “tasa de error de símbolo” y es abreviada SER.

4. Consideraciones Generales Cómo afecta M al Sistema de Comunicaciones? Primer Caso: El incrementar M significa en general, que el sistema transmite mas bits por símbolo (algo positivo), pero también significa generalmente, que la SER se incrementará si la relación SNR-por-bit se mantiene constante (algo negativo).

5. Consideraciones Generales Cómo afecta M al Sistema de Comunicaciones? Segundo Caso: Para un esquema de modulación dado, tal como PAM, el ancho de banda requerido es inversamente proporcional a log 2 (M) . Por ejemplo, un sistema de comunicaciones 8-PAM requiere aprox. 1/3 del ancho de banda de un sistema 2-PAM, para la misma tasa de bits (se considera que varía el tiempo de duración del símbolo).

6. DILEMA Este es el DILEMA fundamental en el diseño de sistemas de comunicación: eficiencia del ancho de banda (la tasa de datos en bits/sec dividida para el ancho de banda requerido en Hz ) versus SNR-por bit .

7. Ejemplo del Dilema Suponga que queremos transmitir 6000 bits/sec a  b-av /N o = 10 dB . Podemos usar sistemas 2-PAM , 4-PAM , o 8-PAM . Cuál es el DILEMA?

8. Ejemplo del Dilema 8-PAM requiere 1/3 del ancho de banda y produce un mayor SER, para la misma tasa de bits/sec y la misma  b-av /N o 8-PAM necesita 9 dB mas de SNR-por-bit (  b-av /N o ) para obtener el mismo SER (probabilidad de error de símbolo) para la misma tasa de bits/sec. Conclusión: La selección CORRECTA depende de la aplicación.

9. Grafico de SER versus SNR-por-bit La mayoría de los gráficos de SER vs. SNR-por-bit muestran SER en escala logarítmica versus  b-av /N o en dB .

10. Asignando Bits a Símbolos Idea Básica : Algunos errores de símbolo son mas comunes que otros. Se busca que la mayoría de los errores de símbolo comunes causen solo el error de un bit (pg. 358 Haykin). Podemos usar la “Codificación Gray” para constelaciones unidimensionales. Constelaciones con mas dimensiones son mas complejas. En muchos casos resulta imposible tener que puntos vecinos de la constelación difieran en un solo bit.