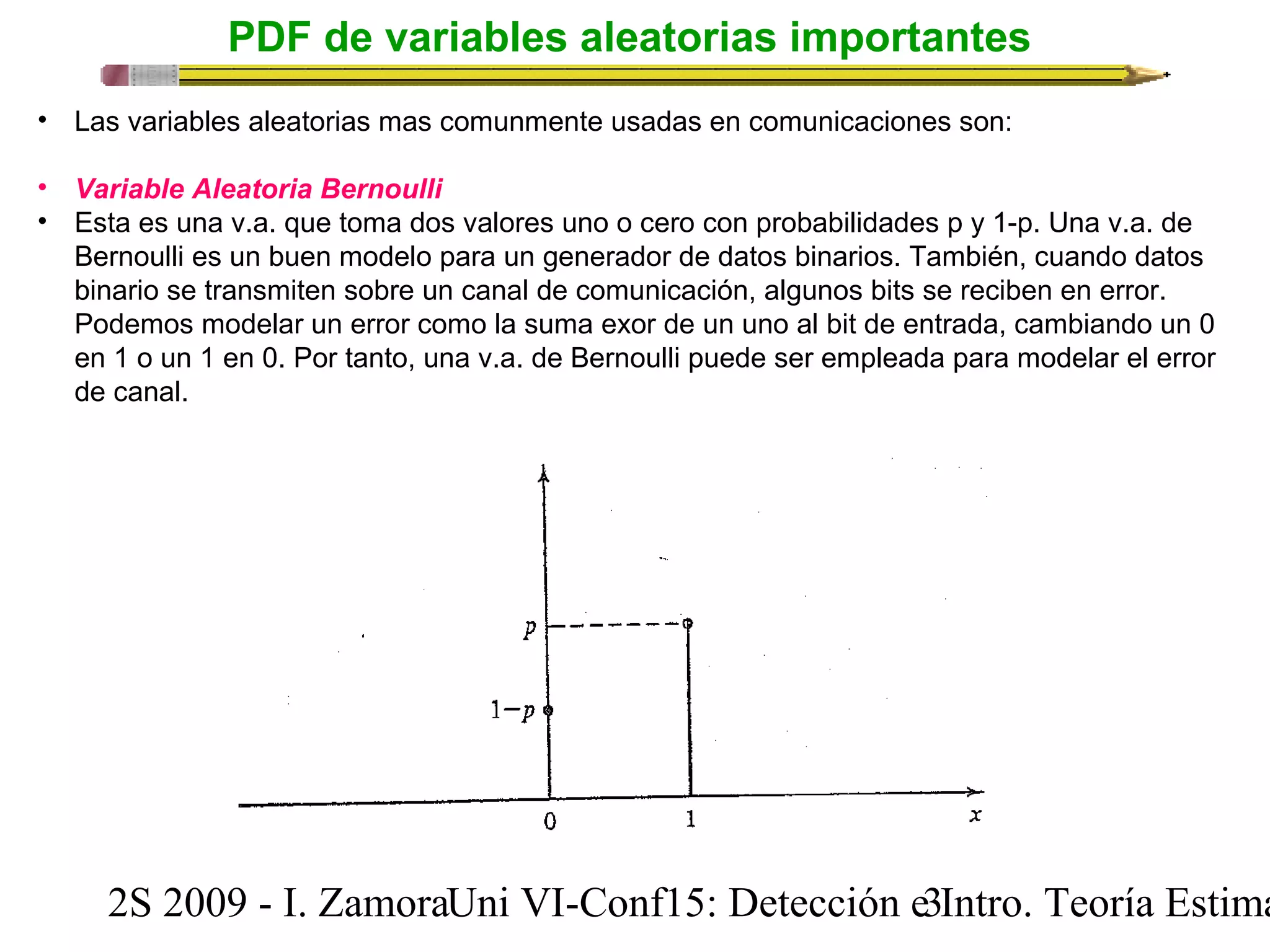
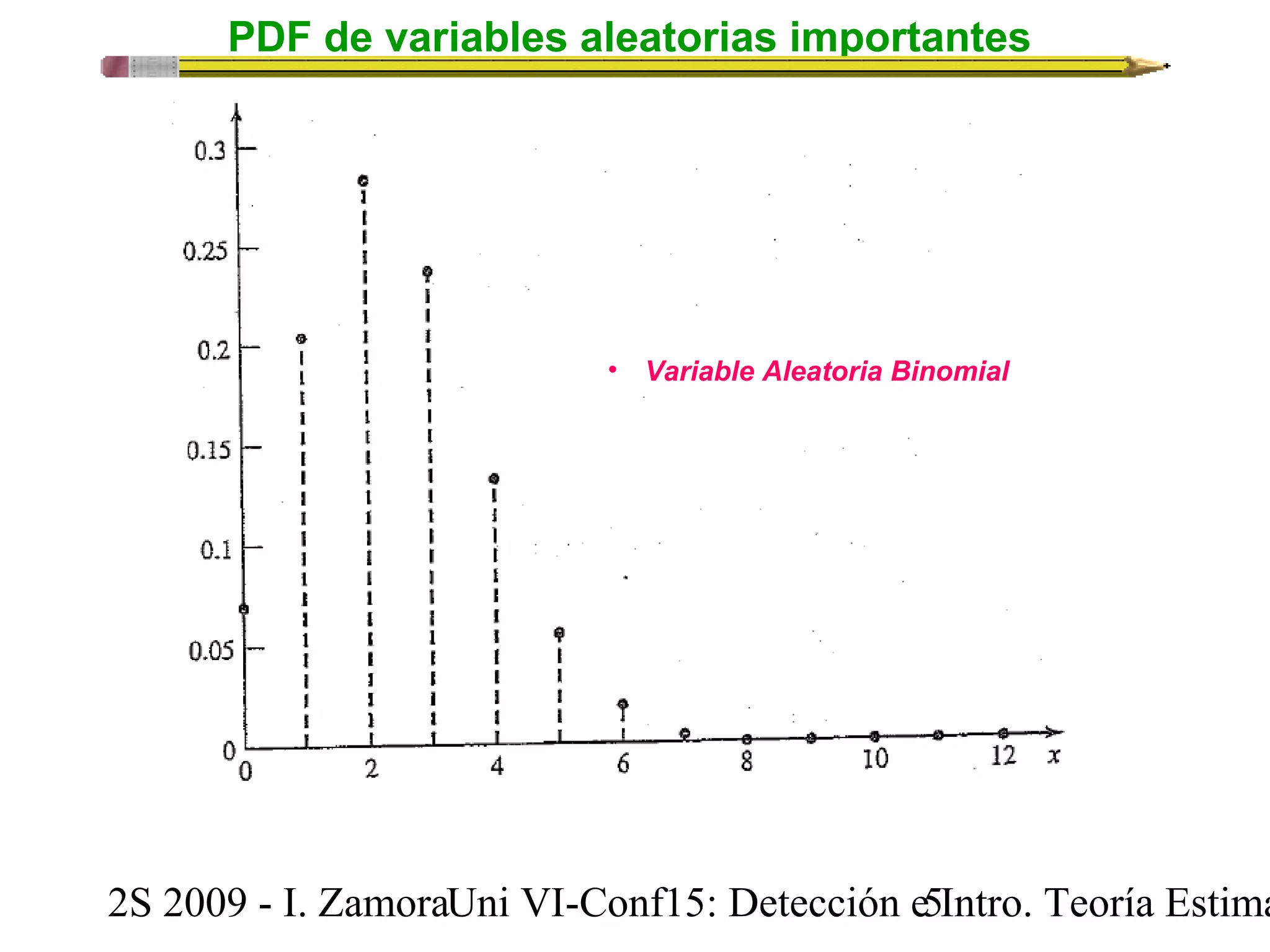
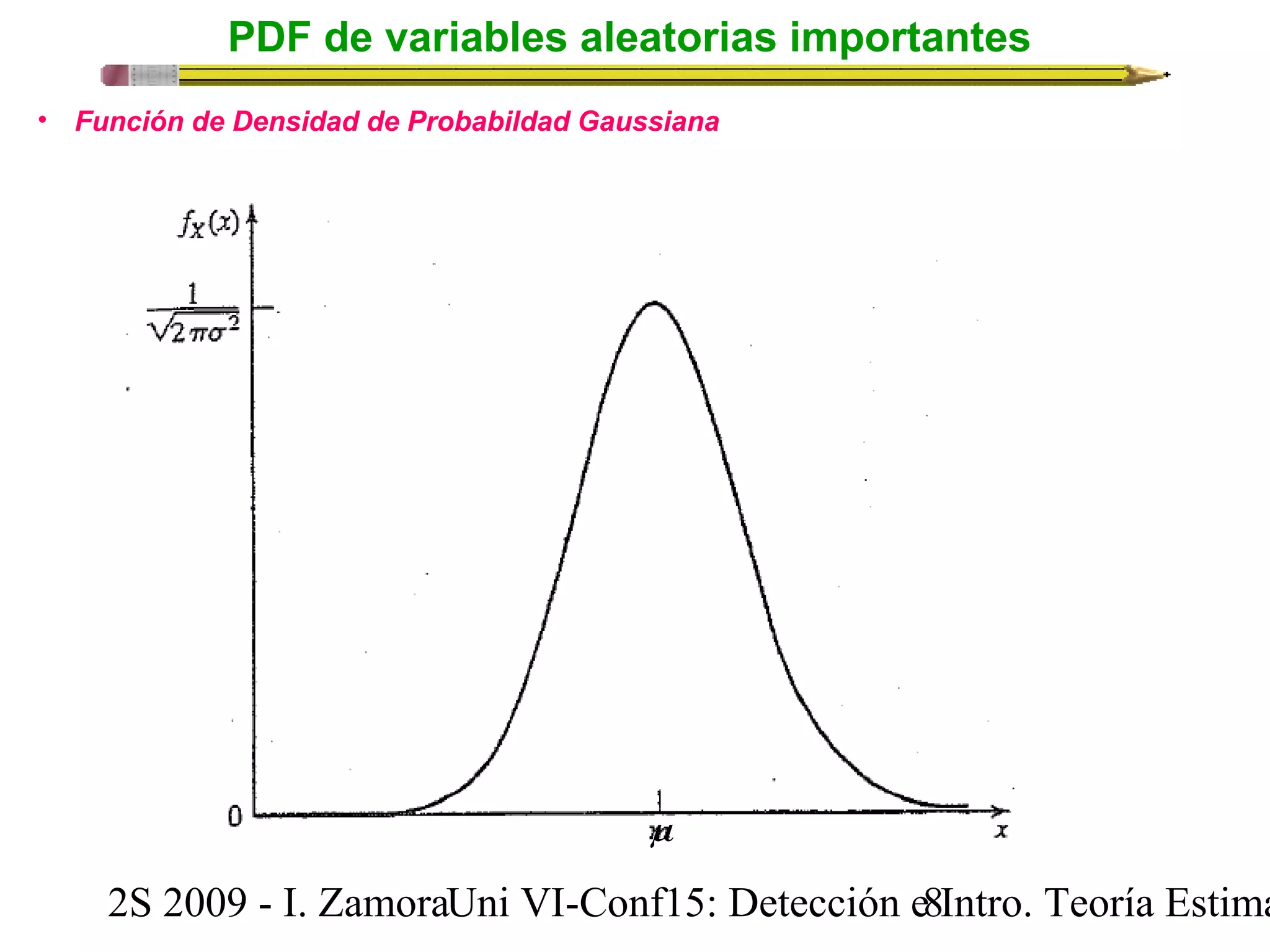
Este documento presenta una conferencia sobre probabilidad de error y tasa de error de bit en señales digitales banda base. Introduce conceptos clave como variables aleatorias comunes en comunicaciones (Bernoulli, binomial, uniforme, gaussiana), y describe el modelo de detección digital binaria, incluyendo el receptor óptimo, el dispositivo de decisión y cálculo de probabilidad de error de bit. Explica las funciones de densidad de probabilidad de las variables aleatorias mencionadas y su importancia para modelar ruido en canales y analizar probabilidad de error en sist








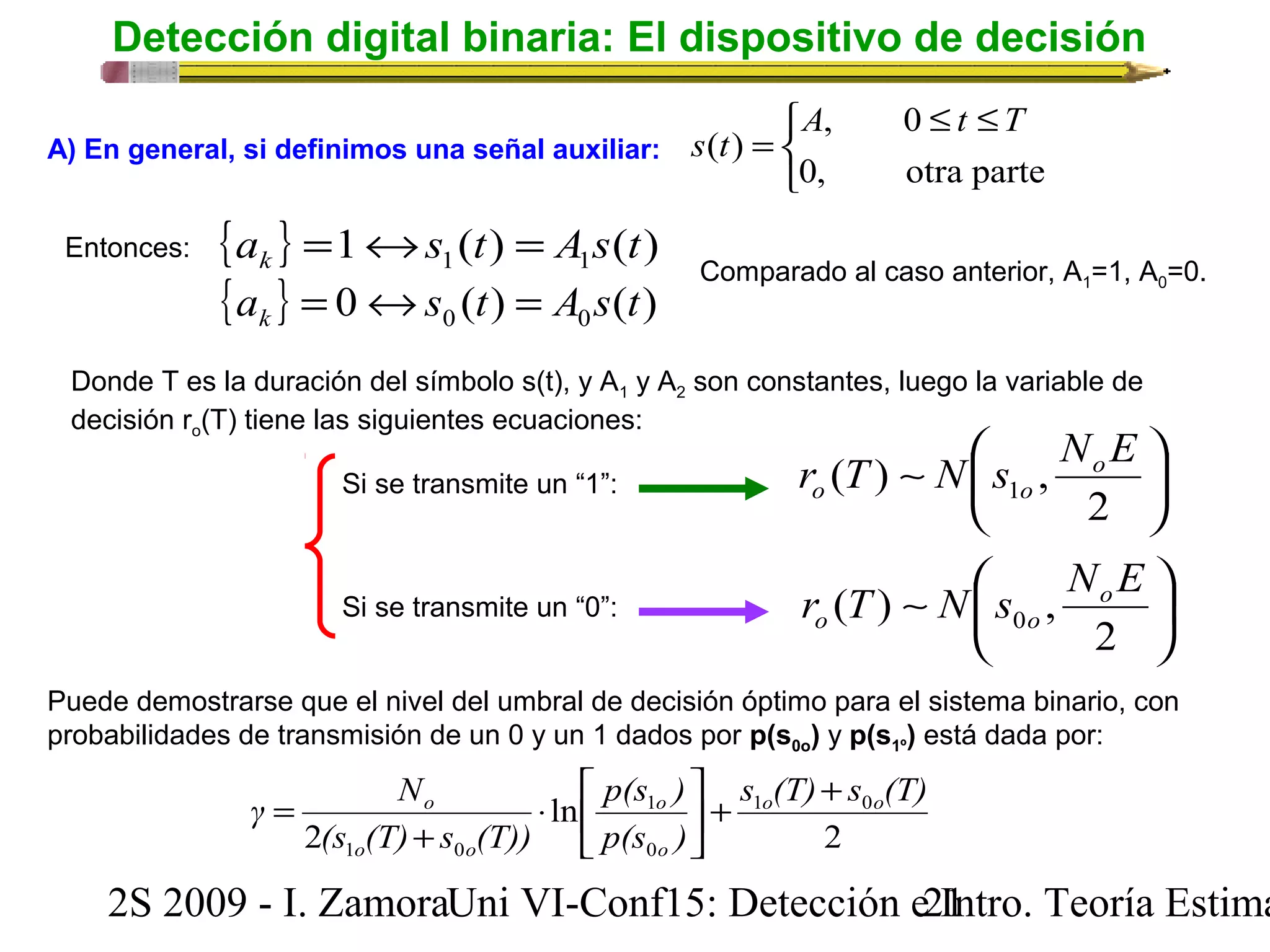
![Detección Digital Binaria: Detección
Partimos de la selección de formas de ondas, o lo que conocemos como la salida del codificador de línea (modulador o
filtro generador de pulsos), para los símbolos binarios 0 y 1:
[{ } 1] [ ( ) ( )] 1 a s t s t k = « =
[{ } 0] [ 0] 0 a = «s (t) = k
Donde s(t) es una función real con duración T, dada por la expresión:
Esta señal es referida como una señalización encendido-apagado
(on-off), o simplemente, de No Retorno a Cero
F.T. Canal Ideal
1 r (t) s (t) n (t) o ko o = +
PSD del AWGN S f = N
f n n N PDF del AWGN
Señal
recibida Secuencia binaria
( ) o
n
A, t T
k k T s(t) s (t) b h (t kT)
= = -
k k
s (t)
ö
æ
2
2
( ) 1
s p s
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e1 I5ntro. Teoría Estimación
(NRZ).
2
î í ì
£ £
=
,
s(t)
0
0
En otra parte
1 0 1 1 0 0 1 1 1 0 1 A0
Estructura del modelo para el análisis de detección de señales binarias AWGN
Filtro de forma
De onda
hT(t) S
Secuencia
binaria PCM
Señal
de ruido
{ } k a
n(t)
Detector:
Filtro Óptimo
Acoplado
Dispositivo
de Decisión:
Comparador
de Umbral
r(t)
{ } k aˆ
t = T
(estimada)
h (t) (t) c = d
s(t) h (t) s(t) c * =
Precodificador
{ } k b
Modulador
s(t)
Canal hc(t)
å ¥
å ¥
=-¥
= -¥
r(t) s(t) h (t) n(t) c = * +
s (t) b h (t kT) k k T = -
Conjunto de formas de
s (t)
ondas para {a} 0
kr (T) s (T) n (T) o ko o = +
÷ ÷ø
ç çè
= exp
- 2
2](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-15-2048.jpg)
![Detección Digital Binaria: el Receptor Óptimo
h (t) (t) c =d
La señal recibida, en vista que se considera un canal AWGN sin memoria, es:
donde n(t) es el ruido aditivo blanco gaussiano (AWGN) con PSD dada
por:
S f = N
( ) o
n
2
r(t) = s(t) +n(t)
El Receptor Óptimo: En vista que la señal recibida r(t) consiste de
ambas señal de información y de ruido, el diseño del receptor
óptimo trata de encontrar el h(t) del filtro acoplado de tal manera
que (SNR)o (razón señal a ruido), a como se define en la ecuación
siguiente, sea la máxima:
s T
( )
2
2
( SNR
) =
ko
o E [ n ( T
)
] o máx
Donde |sko(T)|2 es la potencia instantánea en la señal de salida sko(t) medida en el instante t=T.
Esto, puede demostrarse, se logra seleccionando un filtro acoplado con una función de
tranferencia dada por:
h(t) = s(T -t)
Respuesta al impulso del Filtro Acoplado
(F.T. en el dominio de la frecuencia)
El símbolo recibido a la salida del receptor acoplado es: r (t) s (t) n (t) o ko o = +
El valor muestreado en t=T, del símbolo recibido a la salida del receptor acoplado
es: r (T) s (T) n (T), k , (caso binario) o ko o = + = 0 1
Donde sko (t) es la salida del filtro acoplado para la entrada s(t) y no(t) es la salida del filtro acoplado
para la entrada n(t).
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e1 I6ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-16-2048.jpg)
![Detección Digital Binaria: el Receptor Óptimo
r(t) = s(t) +n(t)
s(t)
n(t)
s(T-t)
s(T-t)
WSS WSS
WSS: Wide Sense Stationary Observe que: h(t) = s(T -t)
Propiedad del Filtro Acoplado:
La razón señal a ruido alcanza un valor máximo dado por:
s (t) s(t) h(t) ko = *
n (t) n(t) h(t) o = *
s T
( )
2
2
SNR ko
2
E
E
= = = con
[ ] N E
o o o
o E n 2
T
N
2
( )
( )
S f = N
( ) o
n
Donde E es la energía de la señal sko(t), que puede obtenerse de:
r(t) s (t) n (t) ko o = +
2
E ò S f df ¥
= ( ) donde S( f ) es la transformada de Fourier de sk(t)
-¥
Y la potencia media de la salida del componente de ruido está dada
por: [ ] ò ò ò ¥
E n2 = S ( f ) 2 df = S ( f ) S ( f ) 2 df = No S f 2 df =
NoE
o no n
-¥
¥
-¥
¥
-¥
2
( )
2
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e1 I7ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-17-2048.jpg)

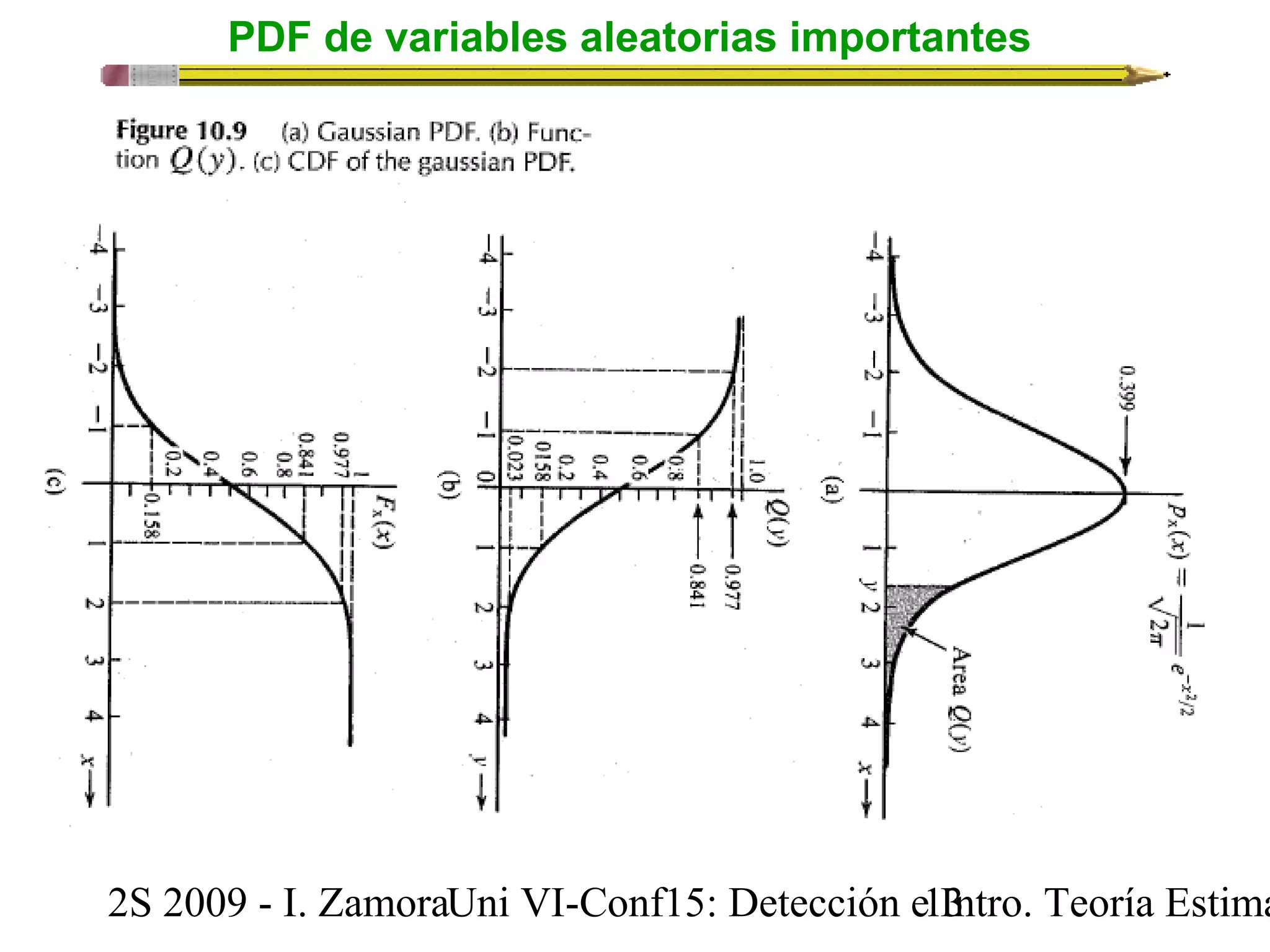
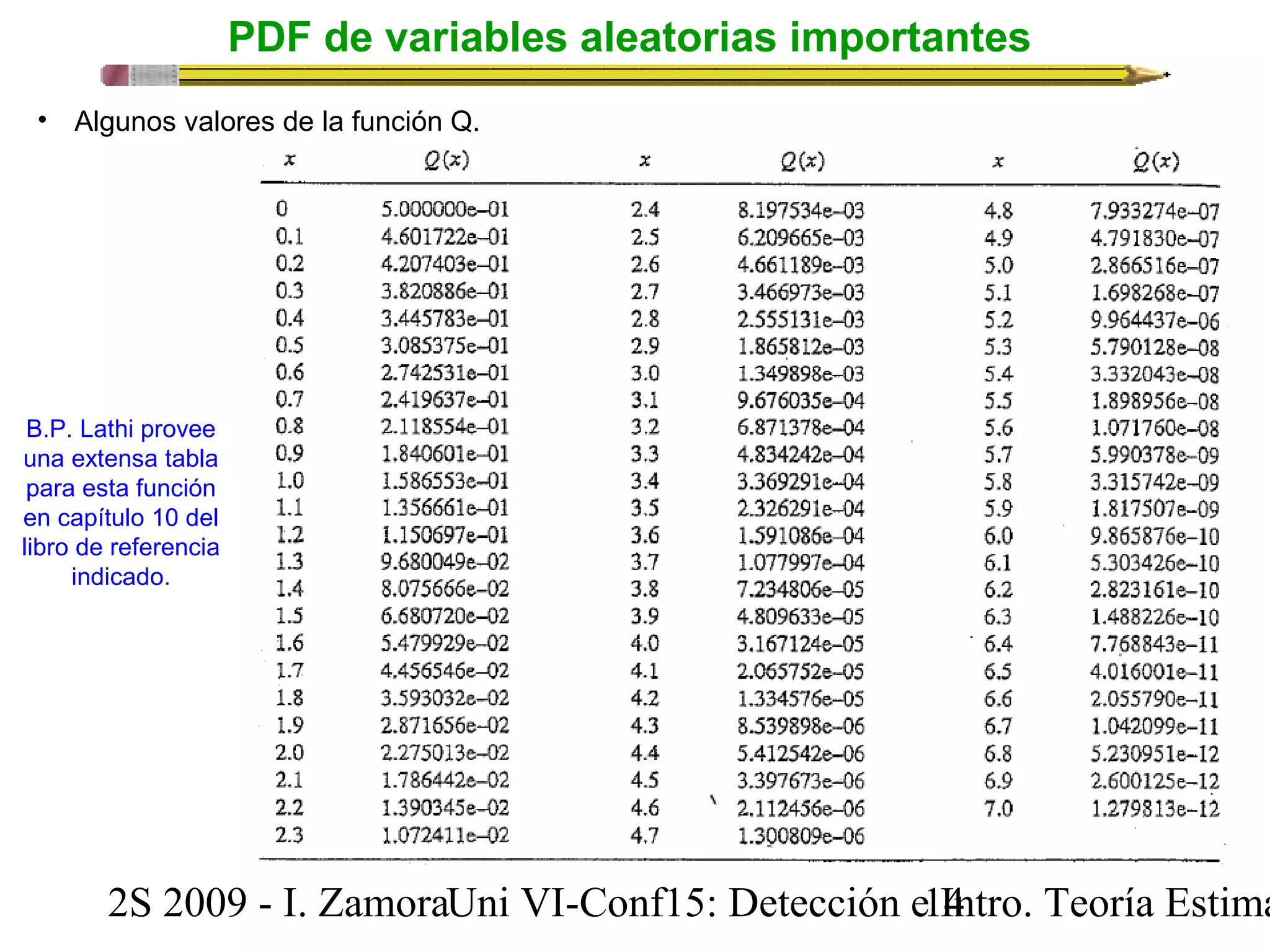
![Detección digital binaria: El dispositivo de decisión
Recordemos que si una variable aleatoria gaussiana X tiene media m y varianza s2, podemos
denotarlos como:
X ~ N(m,s 2 )
( )
ö
÷ ÷ø
ç çè æ - = - 2
2
m
s
f x x X
2
exp
( ) 1
s p
2
PDF de la v.a. X de
tipo gaussiana
A) El componente de ruido, no(t), tiene media cero, así su varianza es igual a su
potencia media, es decir:
s 2 var 2 ( ) 2 ( ) ( ) ( ) ( ) 2
= n T = E n T = S f df = S f H f df no o o no n
Así:
El ruido también
tiene distribución
gaussiana
[ ] [ ] ò ¥
ò -¥
¥
-¥
Media
Varianza
E[n (T)] = 0 o
[ ] [ ] 2
2 var n2 (T) E n2 (T) NoE
no o o s = = =
ö
æ
n
2
( ) 1 exp
n (T) N 0, NoE
o ÷ ÷ø
~ æ
ö çè
÷ø
2
ç çè
= -
N E
N E
f n
o o
N
p
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e2 I0ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-20-2048.jpg)
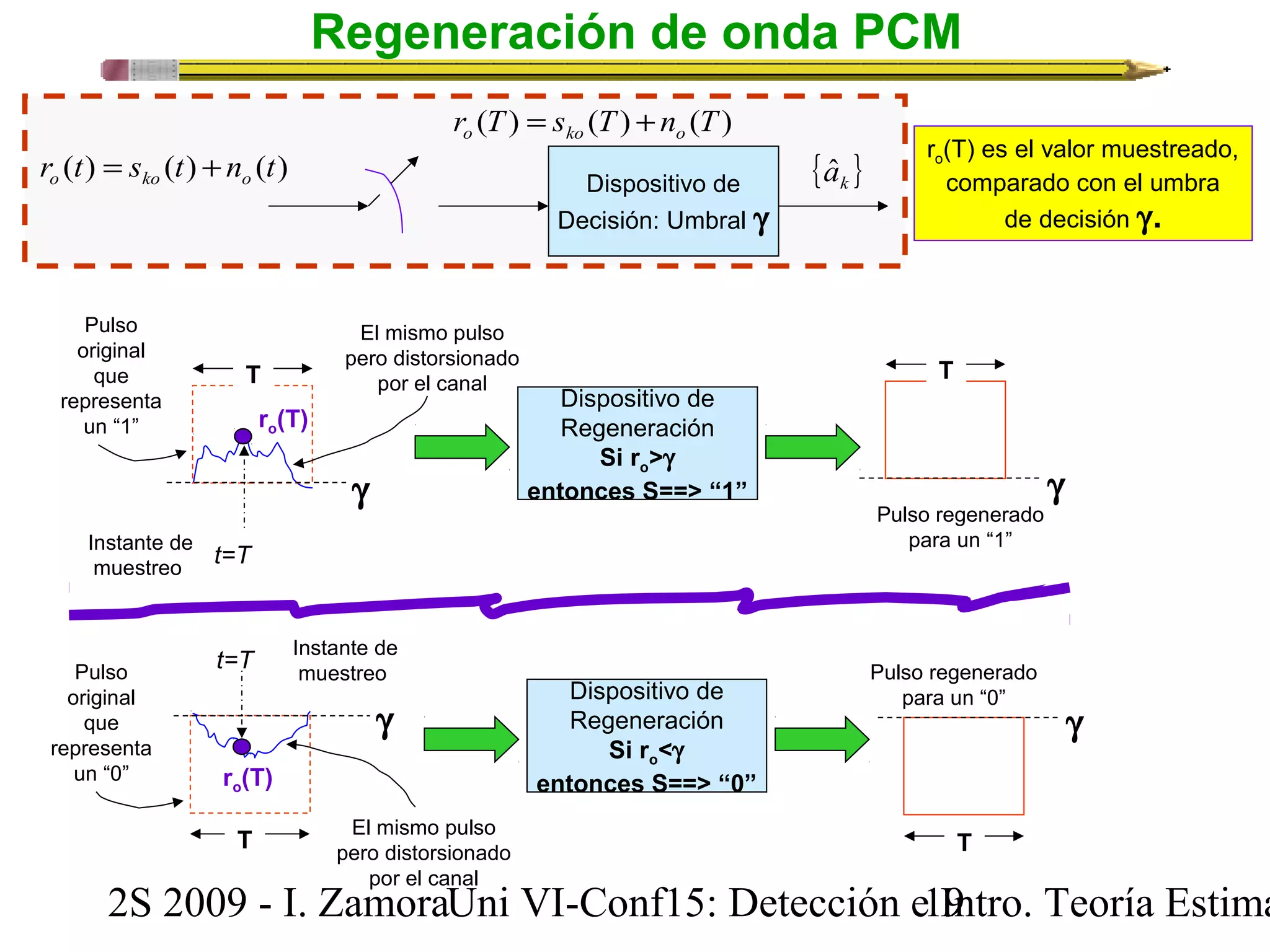
![Detección digital binaria: El dispositivo de decisión
( ) ( ) 1 0 s T s T o o g = +
Si 0 y 1 ocurren con igual probabilidad, es decir son
equiprobables, el umbral de decisión se resume a la expresión: 2
La regla de decisión será una de las dos siguientes hipótesis Hk:
Si r (T) ³g o
, se detecta un “1”. Luego se decide por H1: Un “1” fue enviado, o sea {ak}=1 con s1(t).
Si r o
(T) < g , se detecta un “0”. Luego se decide por H0: Un “0” fue enviado, o sea {ak}=0 con s0(t).
En el caso de señalización NRZ (on-off), tenemos que el umbral está dado por:
g = E
2
Situaciones de error (caso binario):
Se incurre en un error en la recepción cuando se asume una hipótesis incorrecta. Para el caso
Binario tenemos dos situaciones:
P [error de detección de {ak}=1] = P (trasmite {ak}=1 y se detecta {ak}=0)
P [error de detección de {ak}=0] = P (trasmite {ak}=0 y se detecta {ak}=1)
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e2 I2ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-22-2048.jpg)
![Cálculo de Pe
OBERVACIÓN: Cuando M=2, la probabilidad Pb=Pe, por tanto, en esta conferencia, cuando
hablamos de probabilidad de error de bit, también coincide con la probabilidad de error de
símbolo o pulso. Por tanto, trabajos con Pe por conveniencia.
1.- P [error de detección de {ak}=1] = P (trasmite {ak}=1 y se detecta {ak}=0)
1 (1) ( ) e 1 e s P = P s P
donde [ ] ò -¥
= < = g g e s o R S o o P P r T H f r s dr o ( ) ( ) 1 1 1 1
ò -¥
= g
Entonces: Se transmite un “1” pero se
detecta un “0”.
e R S o o P P s f r s dr o (1) ( ) ( ) 1 1 1
( ) 1 1 f r s Ro S o ( ) 0 0 f r s Ro S o
e s1 P e s0 P
Para el caso NRZ on-off:
s T A T E o = 2 =
1 ( )
( ) 0 0 s T = o
( ) ( ) 2
1 0 s T s T A T E g = o + o = =
2 2 2
o0 s g o1 s
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e2 I3ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-23-2048.jpg)
![Cálculo de Pe
Evaluamos la probabilidad de error para el segundo caso de la diapositiva 10:
2.- P [error de detección de {ak}=0] = P (trasmite {ak}=0 y se detecta {ak}=1)
0 (0) ( ) e 0 e s P = P s P
donde [ ] ò¥ = ³ =
P P r ( T ) g H f ( r s ) dr e s 0 o 0 g
R o S 0 o 0
o =
ò¥ e g R S o o P P s f r s dr o (0) ( ) ( ) 0 0 0
Entonces: Se transmite un “0” pero se
detecta un “1”.
( ) 1 1 f r s Ro S o ( ) 0 0 f r s Ro S o
e s1 P e s0 P
Para el caso NRZ on-off:
s T A T E o = 2 =
1 ( )
( ) 0 0 s T = o
( ) ( ) 2
1 0 s T s T A T E g = o + o = =
2 2 2
o0 s g o1 s
2S 2009 - I. ZamoraU n i VI-Conf15: Detección e2 I4ntro. Teoría Estimación](https://image.slidesharecdn.com/lecture15probabilidaddeerroryberensealesbandabasebinaria-141021121847-conversion-gate01/75/Lecture-15-probabilidad-de-error-y-ber-en-senales-bandabase-binaria-24-2048.jpg)





