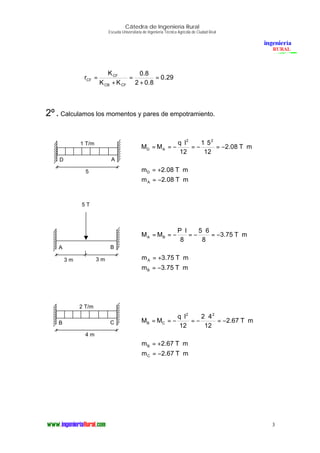
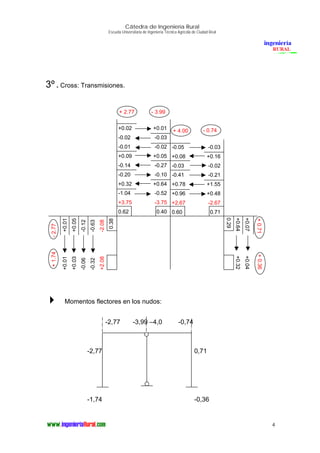
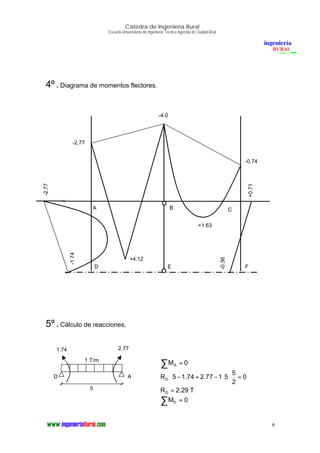
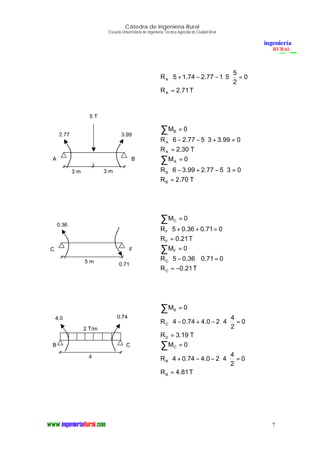
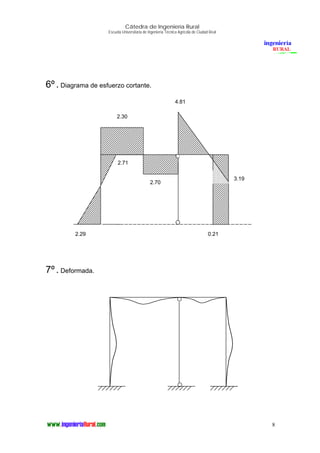
El documento presenta el análisis estructural por el método de Cross de un pórtico. En 3 oraciones o menos: Determina las reacciones, diagramas de momentos flectores y esfuerzos cortantes del pórtico mediante el método de Cross, incluyendo los momentos isostáticos máximos y las reacciones en cada nudo.

1. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
1
Hallar por el método de Cross los diagramas de momentos flectores y
esfuerzos cortantes, así como las reacciones de todas las barras del pórtico de
la figura.
La relación entre los momentos de inercia de las barras es:
321 I3I2I ⋅=⋅=
1º. Determinamos los coeficientes elásticos (βi, Ki y ri).
Nudo A
2
2
AD IE8.0
5
IE4
K ⋅⋅=
⋅⋅
=
2
1
AB IE33.1
6
IE4
K ⋅⋅=
⋅⋅
=
2
1
AB =β
2
1
AD =β
3 3 4
P=5 T
q1=2 T/m
A I1 B
I2 I3
D E
I1 C
I2
F
q2=1T/m
5

2. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
2
38.0
33.18.0
8.0
KK
K
r
ABAD
AD
AD =
+
=
+
=
62.0
33.18.0
33.1
KK
K
r
ABAD
AB
AB =
+
=
+
=
Nudo B
1
1
BA IE67.0
6
IE4
K ⋅⋅=
⋅⋅
=
1
1
BC IE
4
IE4
K ⋅=
⋅⋅
=
0KBE =
2
1
BA =β
2
1
BC =β
0BE =β
40.0
0167.0
67.0
KKK
K
r
BEBCBA
BA
BA =
++
=
++
=
60.0
0167.0
1
KKK
K
r
BEBCBA
BC
BC =
++
=
++
=
0
KKK
K
r
BEBCBA
BA
BE =
++
=
Nudo C
2
1
CB IE2
4
IE4
K ⋅⋅=
⋅⋅
=
2
2
CF IE8.0
5
IE4
K ⋅⋅=
⋅⋅
=
2
1
CB =β
2
1
CF =β
71.0
8.02
2
KK
K
r
CFCB
CB
CB =
+
=
+
=

3. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
3
29.0
8.02
8.0
KK
K
r
CFCB
CF
CF =
+
=
+
=
2º. Calculamos los momentos y pares de empotramiento.
mT08.2m
mT08.2m
mT08.2
12
51
12
lq
MM
A
D
22
AD
⋅−=
⋅+=
⋅−=
⋅
−=
⋅
−==
mT75.3m
mT75.3m
mT75.3
8
65
8
lP
MM
B
A
BA
⋅−=
⋅+=
⋅−=
⋅
−=
⋅
−==
mT67.2m
mT67.2m
mT67.2
12
42
12
lq
MM
C
B
22
CB
⋅−=
⋅+=
⋅−=
⋅
−=
⋅
−==
1 T/m
5
D A
5 T
3 m
A B
3 m
2 T/m
4 m
B C

4. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
4
3º. Cross: Transmisiones.
4 Momentos flectores en los nudos:
-2,77 -3,99 –4,0 -0,74
-2,77 0,71
-1,74 -0,36
+0.02 +0.01
-0.02 -0.03
-0.01 -0.02
+0.09 +0.05
-0.14 -0.27
-0.20 -0.10
+0.32 +0.64
-1.04 -0.52
+3.75 -3.75
0.62 0.40
-0.05 -0.03
+0.08 +0.16
-0.03 -0.02
-0.41 -0.21
+0.78 +1.55
+0.96 +0.48
+2.67 -2.67
0.60 0.71
+0.01+0.01
+0.03+0.05
-0.06-0.12
-0.32-0.63
+2.08-2.08
0.38
+0.07+0.04
+0.64+0.32
0.29
+ 2.77 - 3.99
+ 4.00 - 0.74
+1.74-2.77
+0.71+0.36

5. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
5
4 Momentos isostáticos
mT13.3
8
51
8
lq
M
22
imáx ⋅=
⋅
=
⋅
=
mT87.013.3
2
77.274.1
M
2
MM
M imáx
AD
máx ⋅=+
−−
=+
+
=
mT5.7
4
65
4
lP
M imáx ⋅=
⋅
=
⋅
=
mT12.45.7
2
99.377.2
Mmáx ⋅=+
−−
=
mT4
8
42
8
lq
M
22
máxi
⋅=
⋅
=
⋅
=
mT63.14
2
74.00.4
M
2
MM
M imáx
CB
máx ⋅=+
−−
=+
+
=
1 T/m
5
D A
5 T
3 m
A B
3 m
2 T/m
4
B C

6. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
6
4º. Diagrama de momentos flectores.
5º. Cálculo de reacciones.
0MA =∑
0
2
5
5177.274.15RD =⋅⋅−+−⋅
T29.2RD =
0MD =∑
A
-2.77
-4.0
-0.74
B C
D E F
+4.12
+1.63
-1.74
-0.36
+0.71
-2.77
1 T/m
5
D A
1.74 2.77

7. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
7
0
2
5
5177.274.15RA =⋅⋅−−+⋅
T71.2RA =
0MB =∑
099.33577.26RA =+⋅−−⋅
T30.2RA =
0MA =∑
03577.299.36RB =⋅−+−⋅
T70.2RB =
0MC =∑
071.036.05RF =++⋅
T21.0RF =
0MF =∑
071.036.05RC =−⋅
T21.0RC −=
0MB =∑
0
2
4
420.474.04RC =⋅⋅−+−⋅
T19.3RD =
0MC =∑
0
2
4
420.474.04RB =⋅⋅−−+⋅
T81.4RB =
5 T
3 m
A B
3 m
2.77 3.99
C F
5 m
0.36
0.71
2 T/m
4
B C
4.0 0.74

8. Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
8
6º. Diagrama de esfuerzo cortante.
7º. Deformada.
2.29 0.21
3.19
2.70
2.71
2.30
4.81