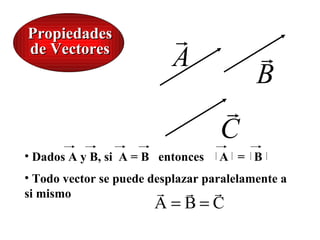
Este documento describe las magnitudes físicas escalares y vectoriales, y explica las propiedades básicas de los vectores como la suma, resta y multiplicación por escalares. También cubre conceptos como el producto escalar y vectorial entre vectores, y cómo representar vectores en sistemas de coordenadas.

1. C 2 MAGNITUDES FÍSICAS. Magnitudes f í sicas escalares y vectoriales. Algebra vectorial. Ejemplos Bibliog. Sears, F ísica universitaria 1999, Hewitt, Física conceptual 1999

2. por su naturaleza Magnitudes físicas Escalares Vectoriales

3. Muchas de las leyes de la física implican no sólo relaciones algebraicas entre cantidades sino también relaciones geométricas . En ocasiones las relaciones geométricas complican las relaciones algebraicas entre las magnitudes físicas. Los vectores permiten esta economía de expresión en numerosas leyes de la Física. A veces la forma vectorial de una ley física nos permite ver relaciones o simetrías que de otro modo estarían veladas por ecuaciones algebraicas engorrosas. Magnitudes físicas Sin embargo si usamos vectores para representar a las magnitudes físicas se requiere entonces de un numero menor de ecuaciones matemáticas para expresar las relaciones entre las magnitudes.

4. Asociadas a propiedades que pueden ser caracterizadas a través de una cantidad Asociadas a propiedades que se caracterizan no sólo por su cantidad sino por su dirección y su sentido Magnitudes físicas Escalares Vectoriales

5. Masa, densidad, temperatura, energía, trabajo, etc Velocidad, fuerza, cantidad de movimiento, aceleración, torque, etc. Magnitudes físicas Escalares Vectoriales

6. Bases para el estudio del movimiento mecánico Se le asocia SR : Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. x(t) y(t) z(t) Observador Sistema de Coordenadas y x z Reloj

7. Movimiento plano

8. Movimiento plano

10. Vectores Notación A Módulo A > 0 A Dirección x y z A p x y

11. Dados A y B, si A = B entonces A = B Todo vector se puede desplazar paralelamente a si mismo Propiedades de Vectores

12. Ley del polígono Suma de Vectores B A R B A C C

13. El vector resultante es aquel que vector que va desde el origen del primer vector hasta el extremo del ultimo

14. Entonces si se tiene los siguientes vectores El vector resultante de la suma de todos ellos será:

16. Propiedades de Vectores A Opuesto -A Nulo 0 = A + ( ) -A Vector unitario

17. Propiedades de la suma de Vectores Ley Conmutativa Ley Asociativa Diferencia A B A -B R

18. Ley conmutativa ¿Como se explica esta regla? Los vectores A y B pueden ser desplazados paralelamente para encontrar el vector suma B R = A+B A B R = B+A (Método paralelogramo) B R = A+B

19. Multiplicación de un vector por un escalar Dado dos vectores Se dicen que son paralelos si

21. Ejemplo 8: Hallar el vector resultante de la suma de los siguientes vectores A B C A B C R = 2

22. Vectores unitarios en el plano x y Vector unitario en la dirección del eje x + Vector unitario en la dirección del eje y +

23. Vectores unitarios en el espacio x y z

24. Representación de un vector x y z A x A y A z A

25. Observaciones: Las componentes rectangulares de un vector dependen del sistema coordenado elegido. La magnitud del vector no cambia. Permanece invariante en cualquier sistema coordenado

26. Determínese la resultante de los siguientes vectores 4u 3u 7u

27. + 8u 4u = 4u

28. Observamos que, cuando los vectores están en la misma dirección podemos determinar fácilmente su magnitud ¿ Que sucede si los vectores no están en la misma dirección ? , ¿ podremos determinar directamente su magnitud ?

29. 4u 3u La magnitud en este caso no puede determinarse directamente , por lo que debemos tratar de buscar otra forma de determinarla

30. 4u 3u 5u 6u 8u 10u

31. 4u 3u 6u 8u

32. 10u 5u Por pitagoras podemos ahora determinar la magnitud del vector resultante

34. 15 u 5 u

35. x y z (x 1 ,y 1 ,z 1 ) (x 2 ,y 2 ,z 2 ) Dados los puntos indicados el vector que los une esta representado por

36. x y z (x 1 ,y 1 ,z 1 ) (x 2 ,y 2 ,z 2 )

37. Producto escalar de dos vectores Proyección de A sobre B Proyección de B sobre A

39. Producto vectorial de dos vectores

40. Demostrar:

41. Determinese la suma de los siguientes vectores : Ejemplo 1:

42. Ejemplo 2: 8m 10m 5m Determine la suma de los vectores indicados x y z

43. Ejemplo 9 Dados los vectores: Determine : a) El producto escalar entre ellos. b)el producto vectorial entre ambos e) el ángulo que forman entre sí. Tarea 9c, 9d y 10