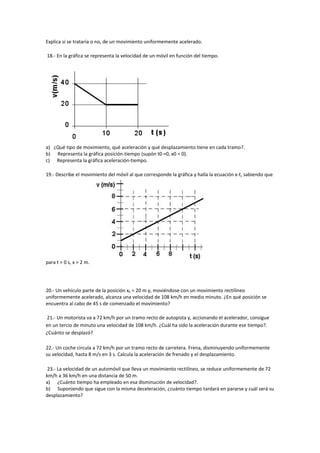
Este documento presenta una serie de problemas de cinemática resueltos. Los problemas involucran conceptos como velocidad, aceleración, desplazamiento y tiempo. Se proporcionan tablas de valores de posición y tiempo, así como gráficas de velocidad contra tiempo y posición contra tiempo para ilustrar diferentes tipos de movimiento, como movimiento uniforme, movimiento uniformemente acelerado y movimiento con aceleración constante.

1. EJERCICIOS CINEMÁTICA 4º ESO 6-10-2010
1.- Un coche inicia un viaje de 495 Km. a las ocho y media de la mañana con una velocidad media de 90
Km/h. ¿A qué hora llegará a su destino?
Solución: a las dos de la tarde.
2.- Un móvil recorre 98 km en 2 h, calcular:
a) Su velocidad.
b) ¿Cuántos kilómetros recorrerá en 3 h con la misma velocidad?
Solución: a) 13,6 m/s; b) 147 km
3.- Un observador se halla a 510 m. de una pared. Desde igual distancia del observador y de la pared, se
hace un disparo; ¿al cabo de cuántos segundos percibirá el observador: a) el sonido directo; b) el eco?
Velocidad del sonido 340 m/s.
Solución: el sonido directo a 0,75 s, y el del eco a 2,25 s.
4.- ¿Cuánto tarda en llegar la luz del sol a la Tierra?, si la velocidad de la luz es de 300.000 km/s y el sol
se encuentra a 150.000.000 km de distancia.
Solución: 8,3 min
5.- Un ladrón roba una bicicleta y huye con ella a 20 km/h. Un ciclista que lo ve, sale detrás de él tres
minutos más tarde a 22 Km/h. ¿Al cabo de cuánto tiempo lo alcanzará?
Solución: 30 minutos.
6.- Dos coches salen a su encuentro, uno de Bilbao y otro de Madrid. Sabiendo que la distancia entre
ambas capitales es de 443 Km. y que sus velocidades respectivas son 78 Km/h y 62 Km/h y que el coche
de Bilbao salió hora y media más tarde, calcular: a) Tiempo que tardan en encontrarse b) ¿A qué
distancia de Bilbao lo hacen?
Solución: tardan en encontrarse 2,5 horas; a 195 km de Bilbao.
7.- Un cohete parte del reposo con aceleración constante y logra alcanzar en 30 s una velocidad de 588
m/s. Calcular: a) Aceleración. b) ¿Qué espacio recorrió en esos 30 s?
Solución: a) 19,6 m/s2; b) 8820 m
8.- Un ciclista inicia el movimiento por una calle con aceleración constante hasta alcanzar una velocidad
de 36 km / h en 10 s. a) ¿Cuánto vale la aceleración?; b) ¿Qué distancia ha recorrido en 10 s?
Solución: a) 1 m/s2; b) 50 m
9.- Un móvil que se desplaza con velocidad constante aplica los frenos durante 25 s y recorre 400 m
hasta detenerse. Calcular:
a) ¿Qué velocidad tenia el móvil antes de aplicar los frenos?
b) ¿Qué desaceleración produjeron los frenos?
Solución: a) v0=32 m/s; b) a=-1,28 m/s2
10.- Un móvil viaja en línea recta con una velocidad media de 1.200 cm/s durante 9 s, y luego con
velocidad media de 480 cm/s durante 7 s, siendo ambas velocidades del mismo sentido:
a) ¿cuál es el desplazamiento total en el viaje de 16 s.?
b) ¿cuál es la velocidad media del viaje completo?
Solución: a) 141,6 m; b) 8,4 m/s
11.- Un ingeniero quiere diseñar una pista para aviones de manera que puedan despegar con una
velocidad de 72 m / s. Estos aviones pueden acelerar uniformemente a razón de 4 m / s2.
a) ¿Cuánto tiempo tardarán los aviones en adquirir la velocidad de despegue?
b) ¿Cuál debe ser la longitud mínima de la pista de despegue?
Solución: a) 18 s; b) 648 m

2. 12.- Un móvil se encuentra en el punto (2,3) en el instante en que empezamos a contar el tiempo y, al
cabo de 20 s en el punto (17,8). ¿Cuánto se ha desplazado?. ¿Qué espacio ha recorrido?. Halla su
velocidad media. Las coordenadas están expresadas en m.
13.- Dada la siguiente tabla de valores:
x(m) 3 6 9 18
t(s) 1 3 8 9
Halla el desplazamiento y la velocidad media entre los instantes t = 3 y t = 9 s.
14.- Dada la siguiente tabla de valores:
x(m) 0 4 10 18
t(s) 0 4 8 12
Calcula la velocidad media entre los instantes 4 y 8 y entre los instantes 8 y 12. Explica si se trata de un
movimiento uniforme o de un movimiento con aceleración.
15.- Dadas las siguientes gráficas:
a) ¿Cuál no puede representar el movimiento de un móvil?. Razónalo.
b) Describe el movimiento del móvil de la otra gráfica.
16.- Un móvil se encuentra en las posiciones y en los instantes indicados en el gráfico.
a) Representa la gráfica x-t. ¿Qué tipo de gráfica es?.
b) ¿De qué tipo de movimiento se trata?. ¿Por qué?.
17.- Dada la siguiente tabla de valores:
v 14 18 24 34
t(s) 0 2 4 6
Calcula la aceleración media:
a) Entre los instantes t = 2 y t = 4 s
b) Entre los instantes t = 4 y t =6s

3. Explica si se trataría o no, de un movimiento uniformemente acelerado.
18.- En la gráfica se representa la velocidad de un móvil en función del tiempo.
a) ¿Qué tipo de movimiento, qué aceleración y qué desplazamiento tiene en cada tramo?.
b) Representa la gráfica posición-tiempo (supón t0 =0, x0 = 0).
c) Representa la gráfica aceleración-tiempo.
19.- Describe el movimiento del móvil al que corresponde la gráfica y halla la ecuación x-t, sabiendo que
para t = 0 s, x = 2 m.
20.- Un vehículo parte de la posición x0 = 20 m y, moviéndose con un movimiento rectilíneo
uniformemente acelerado, alcanza una velocidad de 108 km/h en medio minuto. ¿En qué posición se
encuentra al cabo de 45 s de comenzado el movimiento?
21.- Un motorista va a 72 km/h por un tramo recto de autopista y, accionando el acelerador, consigue
en un tercio de minuto una velocidad de 108 km/h. ¿Cuál ha sido la aceleración durante ese tiempo?.
¿Cuánto se desplazó?
22.- Un coche circula a 72 km/h por un tramo recto de carretera. Frena, disminuyendo uniformemente
su velocidad, hasta 8 m/s en 3 s. Calcula la aceleración de frenado y el desplazamiento.
23.- La velocidad de un automóvil que lleva un movimiento rectilíneo, se reduce uniformemente de 72
km/h a 36 km/h en una distancia de 50 m.
a) ¿Cuánto tiempo ha empleado en esa disminución de velocidad?.
b) Suponiendo que sigue con la misma deceleración, ¿cuánto tiempo tardará en pararse y cuál será su
desplazamiento?

4. 24.- Suponiendo que la aceleración de frenado de un coche es de 3m/s2, determina la distancia mínima
a la que debe mantenerse un coche del que le precede, si circula a 108 km/h y el tiempo de reacción del
conductor es de 0,4 s.
25.- Una empresa automovilística dice que uno de sus modelos tarda 8,7 segundos en llegar a 100
km/h, partiendo del reposo. ¿Con qué aceleración se tiene que mover el vehículo? ¿Qué longitud
mínima tiene que tener una pista para comprobarlo?.
26.- Un objeto que se movía con una velocidad de 72 km/h, acelera y, al cabo de 5 s, alcanza la
velocidad de 40 m/s. Se mantiene con esta velocidad durante 10 segundos y después frena y para en 8
segundos:
a) Construye la gráfica velocidad-tiempo.
b) Calcula la aceleración en cada tramo del movimiento.
c) Calcula el desplazamiento total.
27.- El gráfico siguiente representa el movimiento de un cuerpo.
a) ¿Qué clase de movimiento y qué aceleración tiene en cada tramo?
b) ¿Cuál es el desplazamiento en cada tramo?
8- Un coche arranca y alcanza una velocidad de 64,8 km/h en 10 segundos. Seguidamente inicia un
proceso de deceleración que acaba deteniéndole a los 60 segundos de arrancar.
a) Construye la gráfica velocidad-tiempo.
b) Calcula la aceleración en cada fase del movimiento.
c) Calcula la distancia total recorrida.
28.- Dos móviles pasan por un punto 0, con una diferencia de 2 horas. El primero marcha a 54 km/h y el
segundo a 72 km/h. Calcula el tiempo que tardan en encontrarse y la posición en que se encuentran.
Halla la solución numérica y gráficamente.
29.- En la recta final de una vuelta ciclista, un corredor (A) circula a 28 km/h, seguido a 2,5 m por otro
corredor (B) que se mueve a 22 km/h. La meta está a 290 m de A. Simultáneamente, ambos inician el
sprint. El corredor A lo hace con una aceleración de 0,94 m/s2 y el B con una aceleración de 1,1 m/s2 .
¿Quién gana la etapa?. ¿Con qué diferencia de tiempo llegan?
30.- Escribe las ecuaciones de los dos movimientos representados en la figura. ¿En qué instantes parten
cada uno de los dos móviles?. ¿De qué puntos?. ¿En qué sentido se desplazan? ¿En qué punto se
encuentran?

5. 31.- Dos estaciones A y B, distan entre sí 40 km. A las 8 sale de A un tren que se dirige hacia B con
velocidad constante de 45 km/h. A las 8 y cuarto sale de B otro tren que se dirige hacia A, a 60 km/h.
Escribe las ecuaciones de los movimientos de ambos, tomando la estación A como origen de
coordenadas y sentido positivo el de A a B. Halla en qué punto se cruzan.
32.- Calcula la aceleración y el desplazamiento realizado en 20 s por los móviles cuyas gráficas se
representan en la figura.
33.- Un automóvil y un camión están separados por una distancia de 50 m. El camión se está moviendo
con una velocidad constante de 54 km/h. El automóvil, que se encontraba parado, arranca con una
aceleración de 1,6 m/s2, que se mantiene constante. Determina el instante y la posición en que el
automóvil alcanza al camión. Hazlo gráfica y numéricamente. ¿Qué velocidad lleva el automóvil en el
momento del encuentro?.
34.- De dos puntos A y B, que distan
entre sí 200 m salen simultáneamente
dos móviles. El que sale de A tiene una
velocidad inicial de 5 m/s y se dirige
hacia B con aceleración constante de 1
m/s2. El que sale de B va hacia A con
movimiento uniforme, a 12 m/s. Escribe
las ecuaciones de ambos movimientos
tomando idénticos elementos de
referencia. Halla en que punto se
cruzan. Dibuja las gráficas v-t y x-t para
ambos móviles (Los dos móviles en la
misma gráfica).
35.- El coche A está detenido frente a un semáforo. Se enciende la luz verde y arranca.
Simultáneamente, otro coche B lo adelanta a velocidad constante. Las gráficas v-t de sus movimientos
son:
a) ¿Qué tiempo tarda el coche A en tener la velocidad del B?
b) ¿En qué instante alcanza A a B? ¿A qué distancia del semáforo?
36.- Un cuerpo que se deja caer libremente desde cierta altura, tarda 10 segundos en llegar al suelo.
¿Desde qué altura se dejó caer?. ¿Cuál es su velocidad cuando llega al suelo?
37.- Se deja caer una pelota desde una altura de 20 m. ¿Cuánto tarda en llegar al suelo? ¿Con qué
velocidad llega?

6. 38.- Si dejamos caer un objeto desde 50 m de altura:
a) ¿Cuál será su posición y la distancia recorrida a los 3s de haberlo soltado? ¿Qué velocidad lleva en
ese instante?
b) ¿Cuánto tarda en llegar al suelo?. ¿Con qué velocidad llega?
39.- Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 30,0 m/s. Halla:
a) Posición que ocupa y velocidad al cabo de 1 s.
b) La altura máxima que alcanza y el tiempo empleado.
c) Velocidad cuando llega al suelo y tiempo total empleado.
d) ¿Qué relación hay entre los tiempos calculados en los apartados b y c?
e) ¿Cómo son las velocidades de partida y de llegada?.
40.- Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 39,2 m/s. Halla:
a) El tiempo que tarda en llegar al punto más alto.
b) La altura máxima que alcanza.
c) El tiempo que tarda en alcanzar la altura de 50 m. Explica el significado de las dos soluciones que se
obtienen.
d) La velocidad que lleva a los 50 m de altura.
e) La velocidad con que regresa al punto de partida.
41.- a) ¿Qué tipo de movimiento tiene un objeto que se lanza verticalmente hacia arriba? ¿Hasta
cuándo sube?
b) Cuando vuelve a bajar, ¿qué velocidad tiene al llegar al punto de partida?
c) El tiempo que le lleva subir es igual, mayor o menor que el tiempo que le lleva bajar?
42.- Se lanza un objeto, verticalmente hacia arriba, con una velocidad inicial de 49 m/s. Halla:
a) El tiempo que tarda en llegar al punto más alto.
b) La altura máxima que alcanza.
c) ¿En qué posición se encuentra a los 7 s? Explica el resultado.
43.- Un método que puede utilizarse para determinar la profundidad de una sima consiste en dejar caer
una piedra y contar el tiempo que transcurre hasta que se oye su choque con el fondo. Supón que,
realizada la experiencia hemos obtenido un tiempo de 4 s. Calcula la profundidad de la sima, teniendo
en cuenta que la velocidad del sonido es 340 m/s.
44.- Un coche marcha a 45 Km/h y apretando el acelerador se logra que al cabo de medio minuto se
ponga a 90 Km/h. Calcular la aceleración del vehículo y el espacio recorrido en ese tiempo
(sol: a= 0,4 m/s2 ; s= 564 m).
45.- Un automóvil, partiendo del reposo, acelera uniformemente para alcanzar una velocidad de 20 m/s
en 250 m de recorrido; a partir de este instante y manteniendo constante la velocidad recorre una
distancia de 1500 m, para detenerse a continuación en 50 m, mediante un movimiento uniformemente
retardado, caracterizado por una aceleración negativa de 400 cm/s2. Determinar los tiempos empleados
en cada una de las tres fases del movimiento y dibujar la representación gráfica de la velocidad en
función del tiempo.
(Sol: t1= 25 s; t2= 75 s; t3 = 5s)
46.- Dos cuerpos, A y B, separados por una distancia de 2 Km, salen simultáneamente en la misma
dirección y sentido, ambos con MRUA, siendo la aceleración del más lento, el B, de 0,32 m/s2. El
encuentro se realiza a 3,025 Km de distancia del punto de partida de B. Calcular:
a) El tiempo invertido por ambos móviles
b) La aceleración de A.
c) Las velocidades de ambos en el instante del encuentro

7. (Sol: t= 1375s; a= 0,00053 m/s2; vA= 7,3 m/s; vB= 4,4 m/s)
47.- Un coche lleva una velocidad de 72 Km/h y los frenos que posee son capaces de producirle una
deceleración máxima de 6 m/s2. El conductor tarda 0,8 segundos en reaccionar desde que ve un
obstáculo hasta que frena adecuadamente. ¿A qué distancia ha de estar el obstáculo para que el
conductor pueda evitar el choque en las circunstancias citadas? (sol: 49,3 m)
48.- Desde un punto situado a 10 m sobre el suelo se lanza verticalmente hacia arriba una piedra con
una velocidad de 30 m/s. ¿Con qué velocidad llegará al suelo?(sol: 33,17 m/s)
49.- Un cuerpo es lanzado verticalmente hacia arriba con una velocidad inicial de 20 m/s. Calcular:
a) La altura máxima que alcanzará
b) El tiempo que tarda en alcanzar dicha altura
c) El tiempo mínimo que tarda en alcanzar una velocidad de 10 m/s. (tomar g=10)
(Sol: h= 20m, t =2s; t=1 s.)
50.- Dos proyectiles se lanzan verticalmente hacia arriba con 2 segundos de intervalo, el primero con
una velocidad inicial de 50 m/s y el segundo con velocidad inicial de 80 m(s. ¿Cuál será el tiempo
transcurrido hasta que los dos se encuentren? ¿A qué altura sucederá? ¿Qué velocidad tendrá cada uno
en ese momento?
(Sol: t= 1,62; t= 3,62; h= 116,74; v1= 14,52; v2= 64,12 m/s)
51.- Un avión despega de la pista de un aeródromo después de recorrer 1000 m. Si la velocidad del avión
en el momento de despegar es de 120 Km/h, determinar:
La aceleración que tiene en ese momento
a) El tiempo que tarda en despegar
b) La distancia que recorre en el último segundo antes de despegar
52.- Un avión recorre 1200 m a lo largo de la pista antes de detenerse al aterrizar. Suponiendo que la
deceleración es constante, calcular:
a) La deceleración en la pista si aterriza a 100 Km/h
b) El tiempo que tarda en pararse desde que aterrizó
c) El espacio que recorre en los 10 primeros segundos
53.- Se dispara verticalmente un proyectil con velocidad de 250 m/s; al cabo de un segundo se dispara
otro proyectil con la misma arma. Calcular:
a) La altura a que se encuentran
b) El tiempo que tardan en encontrarse
c) La velocidad de cada proyectil en ese momento
54.- A intervalos iguales de 1/4 de segundo se desprende 4 gotas de un grifo. Cuando se desprende la
última gota, hallar las distancias que separan a las 4 gotas.
55.- Una polea de 2 dm de diámetro gira con una velocidad de 9,8 m/s. Hallar el número de vueltas que
da por minuto y su velocidad angular
56.- Una rueda da 3000 r.p.m. Calcular en rad/s la velocidad angular de la rueda y la velocidad lineal de
un punto de la periferia si tiene de diámetro 10 cm.
57.- Un ciclista recorre una pista circular de 60 m de diámetro con la velocidad de 28 Km/h. Calcular:
a) La velocidad del ciclista en m/s
b) La velocidad angular en rad/s

8. 58.- Un móvil tiene un período de 4 s. Calcula:
a) La frecuencia
b) La velocidad angular
c) La velocidad lineal en un punto situado a 4 m de radio
d) El espacio recorrido a los 5 segundos
e) El ángulo recorrido a los 5 segundos
f) Las r.p.m.
g) El número de vueltas en 10 segundos
59.- Si dejamos caer un objeto desde 50 m de altura:
a) ¿Cuál será su posición y la distancia recorrida a los 3s de haberlo soltado?. .
b) Qué velocidad lleva en ese instante?
b) Cuanto tarda en llegar al suelo?
c) ¿Con qué velocidad llega?
60.- Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 30,0 m/s. Halla:
a) Posición que ocupa y velocidad al cabo de 1 s.
b) La altura máxima que alcanza y el tiempo empleado.
c) Velocidad cuando llega al suelo y tiempo total empleado.
d) Qué relación hay entre los tiempos calculados en los apartados b y c?
e) Como son las velocidades de partida y de llegada?
61.-Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 39,2 m/s. Halla:
a) El tiempo que tarda en llegar al punto más alto.
b) La altura máxima que alcanza.
c) El tiempo que tarda en alcanzar la altura de 50 m. Explica el significado de las dos soluciones
qué se obtienen.
d) La velocidad que lleva a los 50 m de altura.
e) La velocidad con que regresa al punto de partida.
62.- De dos puntos A y B, que distan entre si 200 m salen simultáneamente dos móviles. El que sale de
A tiene una velocidad inicial de 5 m/s y se dirige hacia B con aceleración constante de 1 m/s2. El que sale
de B va hacia A con movimiento uniforme, a 12 m/s. Escribe las ecuaciones de ambos movimientos
tomando idénticos elementos de referencia. Halla en qué punto se cruzan. Dibuja las
gráficas v-t y x-t para ambos móviles (Los dos móviles en la misma grafica).
63.- El coche A esta detenido frente a un semáforo. Se enciende la luz verde y arranca.
Simultáneamente, otro coche B lo adelanta a velocidad constante. Las graficas v-t de sus movimientos
son:
a) Qué tiempo tarda el coche A en tener la velocidad del B?
b) En qué instante alcanza A a B? .A qué distancia del semáforo?
64.- Un disco gira a 33 r.p.m. (revoluciones por minuto). Expresa la velocidad angular en rad/s. Calcula
la velocidad lineal de un punto de la periferia si su radio es de 15 cm.
65.- Los puntos de la periferia de una rueda, que esta girando, tienen una velocidad de 54 km/h. Si la
rueda tiene un radio de 40 cm. .Cual es su velocidad angular en rev/min?
66.- Calcula la velocidad angular en rad/s de las agujas horaria, minutero y segundero de un reloj.

9. 67.- Se lanza un cuerpo verticalmente hacia arriba de forma tal que al cabo de 4 s regresa al punto de
partida. Calcular la velocidad con que fue lanzado.
Sol: 20 m/s.
68.- Un coche va por una carretera recta a velocidad constante. Entra en una población y tiene que
reducir su velocidad constantemente hasta un valor mitad que el inicial. A continuación se encuentra
con un semáforo en rojo que lo obliga a pararse. Arranca de nuevo y sigue hasta atravesar la población,
momento en que de nuevo acelera hasta adquirir la velocidad que tenía antes de entrar en el pueblo.
Representa la gráfica de la velocidad frente al tiempo.
69.- Se deja caer una piedra desde 20 m de alto. Calcula la distancia que hay hasta el suelo desde el
punto en el cual la velocidad de la piedra es la mitad de la que tiene al llegar al suelo.
Sol: 15 m
70.- Calcula la altura de caída de un cuerpo en el vacío, sabiendo que en recorrer la primera mitad de
dicha altura empleó 5 segundos menos que en recorrer la segunda.
Sol: 286 metros
71.- El tiempo de reacción típico de un conductor es de 0,5 s. Supongamos que dicho conductor circula a
una velocidad de 72 km/h. En un momento determinado, se cruza un niño que se encuentra a 40 metros
por delante de su coche. Al pisar el freno, comunica una aceleración de frenado de 10 m/s2. Determina:
a) ¿Qué distancia recorre el coche desde que el conductor ve al niño hasta que pisa el freno?
b) ¿Qué distancia recorre el coche desde que pisa el freno hasta que el coche se detiene
completamente?
c) ¿Atropellará al niño?
Sol: a) 10 m; b) 20 m; c) No
72.- Dada la gráfica s-t del
movimiento de un cuerpo:
a) Indica el tipo de
movimiento en cada tramo;
b) Calcula la velocidad en cada
tramo;
c) Calcula el espacio total
recorrido.
73.- Esta es la gráfica v-t
para un móvil. Señala:
a) Tipo de movimiento en cada
tramo;
b) La aceleración en los tramos B
y C;
c) El espacio total recorrido.