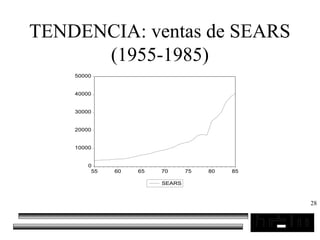
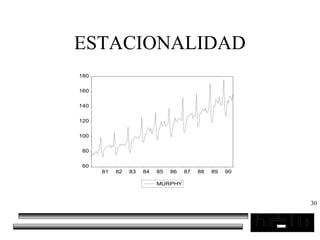
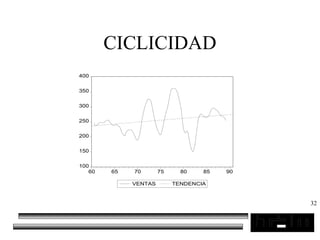
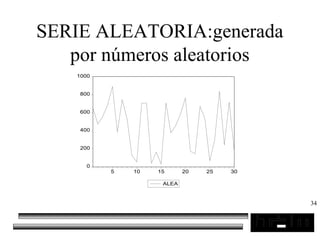
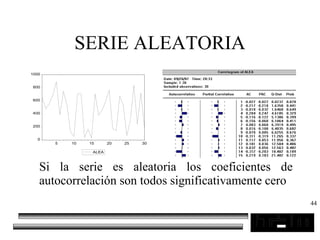
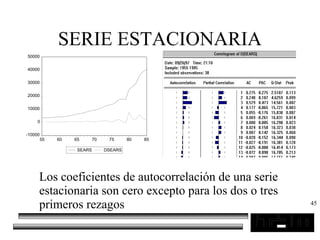
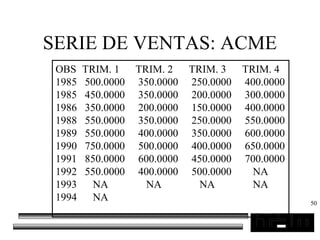
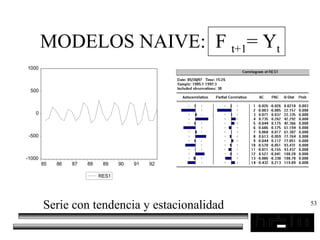
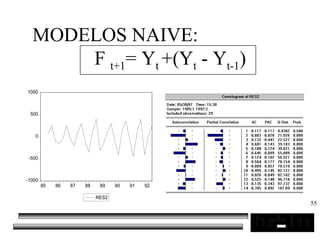
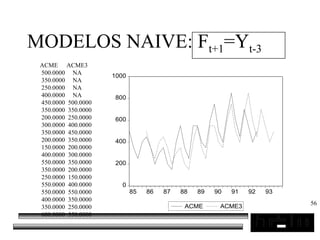
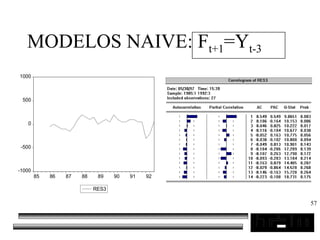
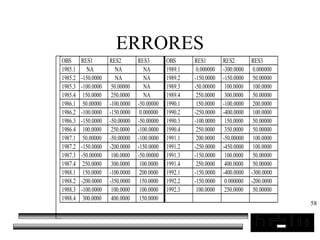
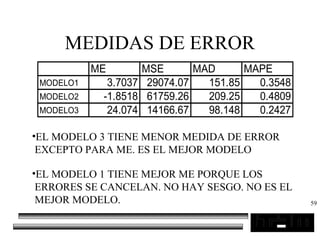
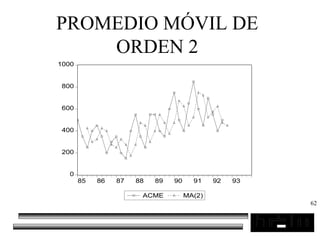
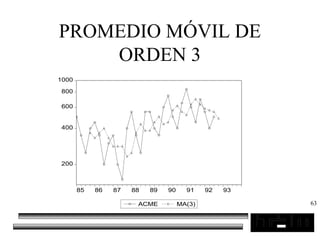
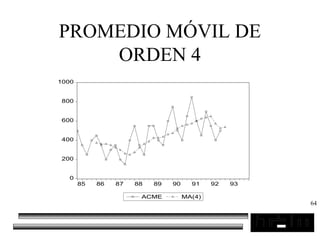
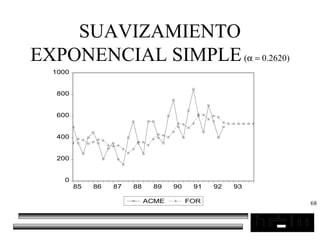
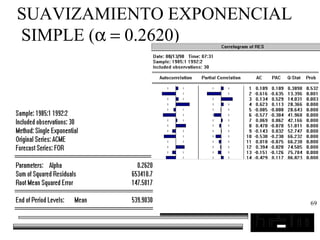
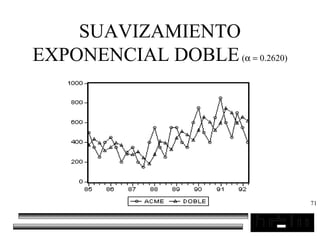
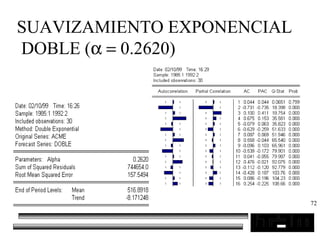
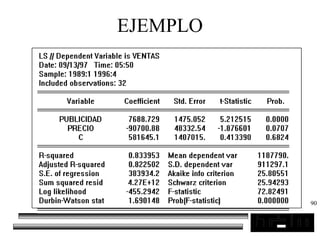
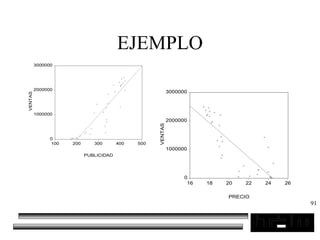
El documento trata sobre los pronósticos empresariales. Explica que un pronóstico es una estimación cuantitativa o cualitativa de factores futuros basada en información pasada o presente. Las empresas deben pronosticar factores incontrolables como la demanda para decidir sobre factores controlables como la producción. El objetivo del pronóstico es reducir la incertidumbre anticipando eventos probables para facilitar la toma de decisiones. Se clasifican los pronósticos por horizonte temporal, área empresarial y técnicas cualitativas versus