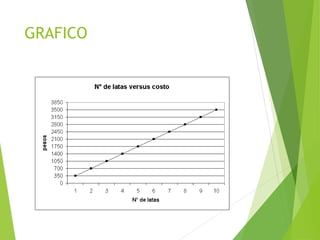
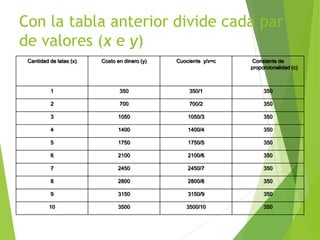
Este documento define la proporcionalidad directa y ofrece ejemplos para ilustrarla. Según la definición, dos variables x e y son directamente proporcionales si su razón y/x es constante. Esto significa que si una variable aumenta o disminuye, la otra hace lo mismo. Los ejemplos muestran cómo variables como kilómetros y horas, o latas de bebida y costo, varían de manera directamente proporcional. Finalmente, se presentan algunos ejercicios para practicar este concepto.

1. PROPORCIONALIDAD
DIRECTA

2. DEFINICIÓN
 Dos variables x e y son directamente
proporcionales si su razón y/x es
constante. En este caso se dice que las
variables x e y son directamente
proporcionales.
 Dicho de otra manera si una de las
variables aumenta (x), la otra también
aumenta (y); y si una de las variables
disminuye (x), la otra también
disminuye (y).

3. EJEMPLOS
Si un automóvil recorre 100 kilómetros en 3 horas ¿Cuántos kilómetros
recorre en 10 horas?
Solución:
Km
x
Hr
Hr
Km
x
Hr
Hr
xKm
Km
33
.
333
3
10
100
10
3
100







4. Una lata de bebida cuesta 350 pesos. Tienes que comprar 10; por lo tanto,
necesitas 3500 pesos.
Con estos datos tenemos siguiente tabla:
Cantidad de latas (X) Costo en dinero
(Y)
1 350
2 700
3 1050
4 1400
5 1750
6 2100
7 2450
8 2800
9 3150
10 3500
Como se aprecia, tenemos dos variables la
cantidad de latas y el costo en dinero, en
ambas los valores aumentan
y a cada valor le corresponde un valor y
sólo uno en la otra.
El gráfico que describe el comportamiento
de las variables es el siguiente:

5. GRAFICO

6. Con la tabla anterior divide cada par
de valores (x e y)
Cantidad de latas (x) Costo en dinero (y) Cuociente y/x=c Constante de
proporcionalidad (c)
1 350 350/1 350
2 700 700/2 350
3 1050 1050/3 350
4 1400 1400/4 350
5 1750 1750/5 350
6 2100 2100/6 350
7 2450 2450/7 350
8 2800 2800/8 350
9 3150 3150/9 350
10 3500 3500/10 350

7. ALGUNOS EJERCICIOS PARA
PRACTICAR
 Tres metros de género valen $ 800. ¿Cuánto valen
ocho metros del mismo género?
 Una moto recorre 120 metros en 4 segundos. ¿Qué
distancia recorre en 52 segundos, si mantiene su
rapidez constante?

8.  Seis operarios cavan en 1 día una zanja de 80 metros
de longitud. ¿Cuántos metros cavarán, en un día, 42
operarios trabajando las mismas condiciones?
 Teresa trabajó 3 horas y ganó $ 8.100. A esa razón,
¿cuánto tiempo le tomará ganar $ 27.000?