El documento describe un experimento sobre el movimiento parabólico de proyectiles, diseñado para verificar teóricamente las fórmulas aplicadas. Se realizaron dos experimentos que midieron la distancia máxima y el tiempo de vuelo de los proyectiles a diferentes ángulos, utilizando un lanzador de proyectiles y diversos materiales. Los resultados apoyan la aplicabilidad de las ecuaciones del movimiento parabólico en diversos contextos.

1. Movimiento Parab´lico
o
Lanzamiento de Proyectiles
R. Pardo, G. Vargas
Departamento de Ingenier´ıa
Universidad Privada Boliviana
1 de febrero de 2013
Resumen
Con el fin de poder observar con mayor exactitud el movimiento pa-
rab´lico sobre una superficie plana y poder comprobar que las f´rmulas
o o
utilizadas en el an´lisis te´rico eran correctas, se realiz´ un experimento
a o o
dividido en dos partes: El primero, donde se estudi´ la distancia m´xima
o a
y el tiempo de vuelo de un proyectil en diferentes ´ngulos; y en la segunda
a
donde tomamos en cuenta una altura base para primeramente observar las
variaciones en la distancia m´xima del proyectil y finalmente, junto con la
a
constante de la gravedad en nuestra ciudad, poder obtener una velocidad
inicial promedio del respectivo disparo.
1. Introducci´n
o
La composici´n de un movimiento uniforme y otro uniformemente acelerado
o
resulta un movimiento cuya trayectoria es una par´bola.
a
Un MRU horizontal de velocidad Vx constante.
Un MRUA vertical con velocidad inicial Vo hacia arriba.
Este movimiento est´ estudiado desde la antiguedad. Se recoge en los libros m´s
a a
antiguos de bal´ıstica para aumentar la precisi´n en el tiro de un proyectil.
o
Denominamos proyectil a todo cuerpo que una vez lanzado se mueve solo bajo
la aceleraci´n de la gravedad. [V´ase la Figura 1] [2]
o e
No se toma en cuenta:
La rotaci´n de la Tierra.
o
El cambio de gravedad.
La forma del proyectil.
La fricci´n del aire.
o
La curvatura de la Tierra.[3]
1

2. Figura 1: Movimiento Parab´lico
o
2. Marco Te´rico
o
Se denomina movimiento parab´lico al desplazamiento realizado por un ob-
o
jeto cuya trayectoria describe una p´rabola. Corresponde con la trayectoria ideal
a
de un proyectil que se mueve en un medio que no ofrece resistencia al avance y
que est´ sujeto a un campo gravitatorio uniforme.
a
Puede ser analizado como la composici´n de dos movimientos rectil´
o ıneos: un
movimiento rectil´ıneo uniforme horizontal y un movimiento rectil´ıneo uniforme-
mente acelerado vertical (gravedad). [1]
2.1. Ecuaciones
x
v= => x = v t (1)
t
Entonces:
x = V o cosα t (2)
1
y = V o sinα t − g t2 (3)
2
De la ecuaci´n (2)
o
x
t= (4)
V o cosα
Para hallar la m´xima distancia se reemplaza la ecuaci´n de tiempo (4) en la
a o
ecuaci´n(3)
o
x 1 x2
y = V o sin( ) − g( 2 2 ) (5)
V o cosα 2 V o cos α
2

3. si Y=0
1 x2
tgα x − g( 2 2 ) = 0 (6)
2 V o cos α
1xg
x(tgα − )=0 (7)
2V o2 cos2 α
1xg
tgα − =0 (8)
2V o2 cos2 α
tgα 2 V o2 cos2 α
=x (9)
g
2 V o2 sinα cosα
xmax = (10)
g
2 V o2 sin2α
xmax = (11)
g
Para hallar la f´rmula de la altura m´xima
o a
g x2
y = tgα x − (12)
2 V o2 cos2 α
Se remplaza la f´rmula de la distancia m´xima (11) en la ecuaci´n (13)
o a o
xmax g xmax 2
ymax = tgα ( )− 2 cos2 α
( ) (13)
2 2 Vo 2
sinα 2sinα cosα V o2 g 2sinα cosα V o2 2
ymax = ( )− ( ) (14)
cosα 2g 2 V o2 cos2 α 2g
Simplificando:
sin2 α V o2 sin2 α V o2
ymax = − (15)
g 2g
sin2 α V o2 1
ymax = (1 − ) (16)
g 2
sin2 α V o2
ymax = (17)
2g
Para el c´lculo del tiempo de vuelo, de la ecuaci´n (3)
a o
g t2
V o t sinα = (18)
2
gt
V o t sinα = (19)
2
2V o sinα
t= (20)
g
Para hallar la f´rmula de velocidad
o
x
t= (21)
v
3

4. 1 2
h= gt (22)
2
Sustituyendo (21) en (22)
1 x2
h= g (23)
2 V2
g x2
V = (24)
2h
3. Materiales
Los materiales utilizados en el experimento son:
1. Perdig´n
o
2. Transportador
3. Lanzador de proyectiles
4. Papel carb´nico
o
5. Papeles en blanco
6. Medidor de ´ngulos
a
7. Soporte universal
8. Cuerda
9. Plomada
10. Cron´metro
o
11. Flex´metro
o
El sistema para el lanzamiento de proyectiles consiste de un ca˜ on con un im´n
n a
para el soporte del proyectil, unido a un transportador de madera el cual se
encunentra pegado a un soporte armado por la combinaci´n de dos bases y tres
o
varas met´licas empleados para la aliaci´n de los mismos. [V´ase la Figura 2]
a o e
Para la obtenci´n de resultados mas precisos se hizo uso de un transportador
o
adicional en la parte inferior de dicho sistema de lanzamiento.
4. Procedimiento
4.1. Experimento 1
En este experimento se analiz´ el tiempo de vuelo y la distancia m´xima de
o a
los proyectiles a diferentes ´ngulos, utilizando el lanzador de proyectiles como
a
mecanismo fundamental, adem´s de papel carb´nico, hojas bond, flex´metro y
a o o
4

5. Figura 2: Lanzador de Proyectiles
Figura 3: Lanzador de Proyectiles
5

6. N. ´
Angulo Tiempo(s) Distancia(cm)
1 15 0.52 160
2 20 0.53 192
3 25 0.55 249
4 30 0.58 273.5
5 35 0.72 309.5
6 40 0.82 316.5
7 45 0.84 318.5
8 50 0.87 321.5
9 55 0.92 305.5
10 60 1.03 282.5
11 65 1.05 243
12 70 1.06 204.5
13 75 1.07 150.5
Cuadro 1: Datos Experimentales
un cron´metro como herramientas adicionales [V´ase la Figura 3]. El experi-
o e
mento consiste en expulsar el perdig´n con el objetivo de que este aterrice sobre
o
el papel carb´nico y de esta forma dejar una marca en la hoja bond la cual nos
o
ser´ util para su posterior medici´n; y paralelamente obtener el tiempo de vuelo
a´ o
haciendo uso del cron´metro.
o
4.1.1. Datos
Seg´n la descripci´n de dicho experimento se obtuvo los siguientes datos:
u o
[V´ase el Cuadro 1]
e
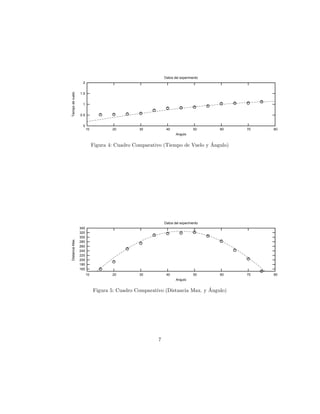
En la (Figura4) podemos comparar los datos obtenidos del experimento con los
datos te´ricos del tiempo de vuelo con respecto a los ´ngulos correspondientes.
o a
En la (Figura5) podemos comparar los datos obtenidos del experimento con
los datos te´ricos de la distancia m´xima con respecto a los ´ngulos correspon-
o a a
dientes.
4.2. Experimento 2
Usando el sistema de lanzamiento de proyectiles desde una superficie alta,
con el objetivo de hallar la velocidad inicial promedio, se desarroll´ cinco lan-
o
zamientos los cuales marcaron cinco diferentes distancias. El m´todo utilizado
e
para este experimento es similar al anterior. Con la ayuda de un flex´metro se
o
realiz´ la medici´n de los puntos marcados en el papel bond por los perdigones.
o o
6

7. Datos del experimento
2
Tiempo de vuelo
1.5
1
0.5
0
10 20 30 40 50 60 70 80
Angulo
´
Figura 4: Cuadro Comparativo (Tiempo de Vuelo y Angulo)
Datos del experimento
340
320
300
Distancia Max.
280
260
240
220
200
180
160
10 20 30 40 50 60 70 80
Angulo
´
Figura 5: Cuadro Comparativo (Distancia Max. y Angulo)
7

8. N. Distancia(cm)
1 260
2 259.8
3 261
4 258.5
5 257
Cuadro 2: Datos Experimentales 2
4.2.1. Datos
Seg´n la descripci´n de dicho procedimiento se obtuvo los siguientes datos:
u o
(Cuadro2)
m
g = 9,775 2 (25)
s
La gravedad en La Paz bolivia esta dada por la constante 9.775, dada por el
Instituto de Investigaciones F´
ısics de la Universidad Mayor de San Andr´s. [4]
e
h = 85,57cm (26)
4.3. C´lculo de Velocidad Inicial
a
Para el c´lculo de la Velocidad inicial promedio se utiliz´ la siguiente ecua-
a o
ci´n
o
g x2
V = (27)
2h
En la ecuaci´n (27) reemplazamos los valores del (Cuadro2)
o
977,5 cm · (260cm)2
s2
V = V = 566,38 (28)
2 · 103cm
977,5 cm · (259,8cm)2
s2
V = V = 565,93 (29)
2 · 103cm
977,5 cm · (261cm)2
s2
V = V = 568,56 (30)
2 · 103cm
977,5 cm · (258,5cm)2
s2
V = V = 563,10 (31)
2 · 103cm
977,5 cm · (257cm)2
s2
V = V = 559,83 (32)
2 · 103cm
566,38 m
s + 565,93 m + 568,56 m + 563,10 m + 559,83 m
s s s s
Vpromedio = ( ) (33)
5
m
Vpromedio = 564,03 (34)
s
8

9. 5. Resultados
Debido a la aproximaci´n de los datos experimentales a los datos te´ri-
o o
cos, se puede concluir que las ecuaciones del movimiento parab´lico son
o
aplicables en distintos medios para diferentes prop´sitos.
o
6. Conclusiones y Recomendaciones
Se debe manejar un buen procedimiento a la hora de tomar las l´ ıneas de
partida, como llegada del proyectil para evitar el margen de error en las
medidas.
Para el calculo de la velocidad promedio en la parte experimental, es
preciso obtener m´s de tres datos para llegar a un resultado mas exacto.
a
Referencias
[1] http://movimientoparabolicokrisia.blogspot.com/
[2] http://recursostic.educacion.es/descartes/web/materiales_
didacticos/comp_movimientos/parabolico.htm
[3] Serway, F´
ısica 1, 5ta Edici´n
o
[4] http://www.scielo.org.bo/scielo.php?pid=
S1562-38232010000100007&script=sci_arttext
A. R. TICONA BUSTILLOS y G. M. RAMIREZ AVILA
9