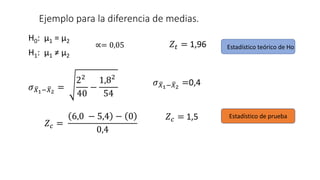
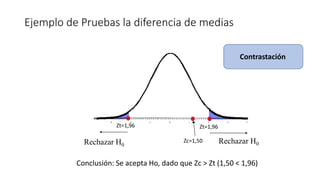
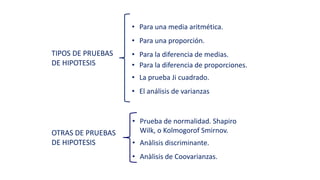
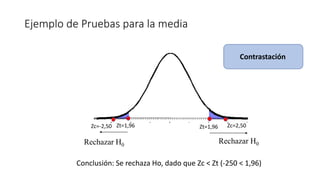
1) La prueba de hipótesis es un procedimiento estadístico para determinar si una hipótesis nula es razonable basado en evidencia de una muestra. Involucra establecer una hipótesis nula y alternativa, seleccionar un nivel de significancia, y decidir si se acepta o rechaza la hipótesis nula. 2) Existen diferentes estadísticos de prueba como z, t, y chi cuadrado que dependen del tipo de prueba y si la desviación estándar es conocida o no.

1. PRUEBA DE HIPOTESIS

2. Hipótesis
Prueba de
Hipótesis
Es una afirmación o conjetura acerca de un
parámetro de una o mas poblaciones y esta sujeta
a verificación.
Procedimiento basado en evidencia de la muestra y
la teoría de las probabilidades para poder
determinar si la hipótesis es una afirmación
razonable .
Prueba de Hipótesis

3. Prueba de Hipótesis
Hipótesis Nula
Es cualquier cosa que se desea probar.
Se denota H0 .
Hipótesis
Alternativa
Es la hipótesis que se acepta cuando la
hipótesis nula es rechazada.
Se denota H1.

4. Prueba de Hipótesis
La Hipótesis Nula se rechaza solo si los datos
ofrecen suficiente evidencia para no
considerarla verdadera.

5. Nivel de significancia
Es la probabilidad de rechazar la Hipótesis Nula cuando es
verdadera
Se denota por α.
Por lo que las muestras son al azar.
Este nivel de significancia permite establecer, con base en
probabilidades un criterio para determinar si se tiene suficiente
evidencia para descartar la Hipótesis Nula

6. Nivel de significancia aceptable
No se desea que la probabilidad de rechazar la Hipótesis Nula
cuando es verdadera sea demasiado alta.
Generalmente las pruebas de Hipótesis se realizan con niveles de
significancia de
5% o 1%

7. ERRORES
Error tipo I
Error tipo II
Se comete cuando se acepta
una hipótesis que es
incorrecta
La probabilidad de cometer
ese error se denota β.
Se comete cuando se rechaza
una hipótesis que es
correcta.
La probabilidad de cometer
ese error se denota α.

8. ERRORES
• Las hipótesis nula y alterna son aseveraciones sobre la
población que compiten entre sí.
• No siempre es posible que las conclusiones sean verdaderas o
correctas.

9. Estadístico de Prueba
Es necesario un valor que sea contrastado contra el valor
critico, o sea, el valor determinado por el nivel de significancia
en una distribución de probabilidad adecuada.
Esto permite establecer una regla para tomar la decisión de
aceptar o rechazar la hipótesis nula

10. 1. Se establece la Hipótesis Nula y la Hipótesis Alternativa.
2. Se selecciona un nivel de significancia para la prueba.
3. Se identifica el estadístico de prueba
4. Se formula una regla para tomar una decisión
5. Se toma la muestra y se llega a una decisión: Se acepta o se
rechaza la Hipótesis Nula.
Pasos para probar una Hipótesis

11. 1. Con n ≥ 30 y con 𝜎 conocida
𝑧 =
𝑥 − 𝜇
𝜎/√𝑛
2. Con n ≥ 30 y con 𝜎 desconocida
𝑧 =
𝑋 − 𝜇
𝑠 /√𝑛
Con n < 30 y con 𝜎 desconocida
𝑡 =
𝑋 − 𝜇
𝑠 /√𝑛
Estadísticos de Prueba

12. TIPOS DE PRUEBAS
DE HIPOTESIS
• Para una media aritmética.
• Para una proporción.
• Para la diferencia de medias.
• Para la diferencia de proporciones.
• La prueba Ji cuadrado.
• El análisis de varianzas
OTRAS DE PRUEBAS
DE HIPOTESIS
• Prueba de normalidad. Shapiro
Wilk, o Kolmogorof Smirnov.
• Anàlisis discriminante.
• Anàlisis de Coovarianzas.

13. Muestra Grande
• En este caso (n>30) se asume distribución normal
• Para pruebas de hipótesis acerca de la media de una
población se emplea el estadígrafo z
• Se determina si la desviación del valor numérico en estudio
es lo suficiente para justificar el rechazo de la hipótesis
nula
 
/
X
z
n




Prueba para la Media

14. 𝑡𝑛−1 =
𝑋 − 𝜇
𝑆
√𝑛
Muestra Pequeña n < 30
 En este caso (n<30) se asume distribución normal.
 Para pruebas de hipótesis acerca de la media de una población se
emplea el estadígrafo 𝑡𝑛−1
tt tabular
tc Calculado
Prueba para la Media pequeña muestra y
σ desconocida

15. Ejemplo de Pruebas para la media
0
-1.96 1,96
a=0.025 a=0.025
X
n

 
z
Rechazar H0 Rechazar H0
 
/
X
z
n




Ejemplo para la Media muestra grande y
σ conocida

16. Ejemplo de Pruebas para la media
𝑍𝑐 =
980 − 1000
8
𝑍𝑐 = -2,50 𝑍𝑡 = 1,96
Se sospecha que una máquina
envasadora de detergentes
necesita ajuste. Dicha máquina
envasa botellas con promedio de
1.000 c.c, y desviación estándar de
80 c.c.
Se tomó una muestra de 100
botellas, de las cuales se obtuvo un
promedio de 980 c.c. de detergente
envasado.
Pregunta: Es cierto que la máquina
continua envasando un promedio
de 1.000 c.c. por botella?
Estadístico de prueba Estadístico teórico de Ho
𝜎𝑋 =
80
100
𝜎𝑋 = 8

17. Ejemplo de Pruebas para la media
Rechazar H0
Rechazar H0
Zt=1,96
Zt=1,96 Zc=2,50
Zc=-2,50
Contrastación
Conclusión: Se rechaza Ho, dado que Zc < Zt (-250 < 1,96)

18. Prueba para la diferencia de Medias
muestras grandes y σ conocida
 En este caso (n>30) asumiendo distribución normal.
 Para pruebas de hipótesis acerca de la diferencia de medias de dos poblaciones
con distribución normal se emplea el estadígrafo z.
𝑍𝑐 =
𝑋1 − 𝑋2 − 𝜇1 − 𝜇2
𝜎𝑋1−𝑋2
𝜎𝑋1−𝑋2
=
𝜎1
2
𝑛1
+
𝜎2
2
𝑛2
Estadístico de prueba para la
diferencia de medias
Error típico para la diferencia de
medias

19. Ejemplo para la diferencia de medias.
Población Muestras Medias Desv. Standar
Población 1 n1= 40 S1 = 2,0
Población 2 n 2 = 54 S2 = 1,8
𝑋1 = 6,0
𝑋2 = 5,4
H0: µ1 = µ2
H1: µ1 ≠ µ2
H0: µ1 = µ2
H1: µ1 < µ2
H0: µ1 = µ2
H1: µ1 > µ2
∝= 0,05
∝= 0,025
En dos poblaciones se desea saber si existe una diferencia estadísticamente
significativa en los salarios de los trabajadores. Los datos correspondientes a
tamaños muestrales, promedios y desviación estándar se presentan en la siguiente
tabla:

20. Ejemplo para la diferencia de medias.
𝑍𝑐 =
6,0 − 5,4 − 0
0,4
𝜎𝑋1−𝑋2
=0,4
𝜎𝑋1−𝑋2
=
22
40
−
1,82
54
𝑍𝑐 = 1,5
H0: µ1 = µ2
H1: µ1 ≠ µ2
∝= 0,05 𝑍𝑡 = 1,96
Estadístico de prueba
Estadístico teórico de Ho

21. Ejemplo de Pruebas la diferencia de medias
Rechazar H0
Rechazar H0
Zt=1,96
Zt=1,96
Zc=1,50
Contrastación
Conclusión: Se acepta Ho, dado que Zc > Zt (1,50 < 1,96)

22. Prueba para la diferencia de proporciones
4. Cálculo de estadístico de prueba
H0: P1 = P2
H1: P1 ≠ P2
1. Plateo de hipótesis.
2. Nivel de significancia y estadístico teórico
3. Obtención de datos muestrales.
α = 0,05; Zt = 1,96
P1, P2, n1 et n2
4. a) Proporción
ponderada de éxito
4. b) Error típico de la
diferencia de
proporciones
𝒁𝒄 =
𝑷1 − 𝑷2 − 𝑷1𝑯0 − 𝑷2𝑯0
𝝈𝑷1−𝑷2
4. c) Estadístico de prueba para
la diferencia de proporciones
https://es.slideshare.net/williamleon20/prueba-de-hipotesis-
para-proporciones-est-ind-clase02

23. Ejemplo para la diferencia de proporciones.
Población Muestras Proporciones
(p)
Proporciones
(q)
Grupo 1 n1= 100
Grupo 2 n 2 = 80
H0: µ1 = µ2
H1: µ1 ≠ µ2
H0: µ1 = µ2
H1: µ1 < µ2
H0: µ1 = µ2
H1: µ1 > µ2
∝= 0,05
∝= 0,025
𝑝1 = 0,90
𝑝2 = 0,70
𝑞1 = 0,10
𝑞2 = 0,30
Con el fin de decidir si un programa de capacitación en técnicas de mercadeo mejora el desempeño
de los asesores comerciales, se estudiaron dos grupos: El grupo 1 que recibió la capacitación y el
grupo 2 que no la recibió. Las proporciones de éxito en los negocios realizados, así como los tamaños
muestrales se presentan en la siguiente tabla.

24. Ejemplo para la diferencia de proporciones.
4. Cálculo de estadístico de prueba
H0: P1 = P2
H1: P1 ≠ P2
1. Planteo de hipótesis.
2. Nivel de significancia y estadístico teórico
3. Obtención de datos muestrales.
α = 0,05; Zt = 1,96
P1 =0,9, P2 =0,7, n1 =100 et n2 = 80
4. a) Proporción
ponderada de éxito
4. b) Error típico de la
diferencia de
proporciones
𝒁𝒄 =
0,9−0,7 − 0
0,06
= 3,33
4. c) Estadístico de prueba para
la diferencia de proporciones
𝑃 =
100∗0,9+80∗0,7
100+80
= 0,81
𝝈𝑷1−𝑷2
=
0,81∗0,19
100
+
0,81∗0,19
80
=0,06

25. Ejemplo para la diferencia de proporciones
Rechazar H0
Rechazar H0
Zt=1,96
Zt=1,96
Zc=3,33
Contrastación
Conclusión: Se rechaza Ho, dado que Zc > Zt (3,33 > 1,96)

26. Bibliografía
• Kazmier L et Diaz A. 1991. Estadística aplicada a administración y economía. 2ª
Ed. McGraw-Hill Interamericana de México, SA.
• Dominick S et Derrick R. 2002. Theory and problems of statistics and
econometrics. 2ª Ed. McGraw-Hill. Serie Schaumʼs. New York.
• Anderson D, Sweeney D et Williams T. 2012. Estadística para negocios y
economía. Cengage learnig. 11ª ed. México.