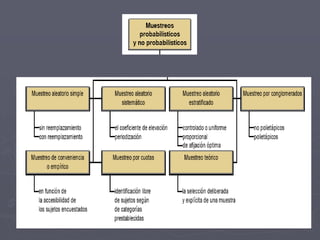
Este documento presenta conceptos básicos sobre cálculos muestrales como población, muestra, parámetro, estadístico, varianza poblacional, inferencia estadística, error muestral y nivel de confianza. Luego explica fórmulas para calcular el tamaño de muestra para estimar la media, proporción y correlación de una población, así como para estudios de casos y controles y cohortes. Finalmente incluye ejemplos numéricos de cálculos de tamaño muestral.

1. IGENC
TEL IA
IN
OFICINA DE
SA
NITARIA
RED ASISTENCIAL LAMBAYEQUE
ESSALUD
Cálculos muestrales
Dr. Cristian Díaz Vélez
Epidemiólogo Clínico
Auditor Médico
cristiandiazv@hotmail.com
cristian.diaz@essalud.gob.pe

2. Conceptos primarios
► Población
► Muestra
► Parámetro
► Estadístico
► Varianza poblacional
► Inferencia estadística
► Error muestral o Tolerancia de error
► Nivel de confianza.

3. Conceptos primarios
► Población: conjunto de individuos o
elementos que cumplen ciertas propiedades
comunes.
► Muestra: subconjunto representativo de
una población.

4. Conceptos primarios
► Parámetro : Son las medidas o datos que
se obtienen sobre la distribución de
probabilidades de la población, tales como
la media, la varianza, la proporción, etc.
► Estadístico. Los datos o medidas que se
obtienen sobre una muestra y por lo tanto
una estimación de los parámetros, es decir
es igual al parámetro pero de la muestra.

5. Conceptos primarios
► Varianza Poblacional. Cuando una
población es más homogénea la varianza es
menor. Generalmente es un valor
desconocido y hay que estimarlo a partir de
datos de estudios previos.
► Inferencia estadística. Inferencias acerca
de la población a partir de una muestra
extraída de la población.

6. Conceptos primarios
► Error Muestral o Tolerancia de error: de
estimación o standard. Es la diferencia entre un
estadístico y su parámetro correspondiente.
Generalmente 5%, en estudios con fármacos
1%.La tolerancia debe ir de la mano de la
prevalencia del estudio en cuestión.
► Nivel de Confianza. Probabilidad de que la
estimación efectuada se ajuste a la realidad.

7. Conceptos primarios
► Ejemplo:
Si por ejemplo estudiamos la prevalencia de
asma bronquial en un estudio donde se
cálculo la muestra con tolerancia de error
del 5% y nivel de significancia del 95% y se
encontró que la prevalencia es de 20%.
Interpretación: hay un 95% de probabilidad
que la prevalencia real este entre 15 y
25%.
Que ocurre si las prevalencias son muy bajas, por ejemplo 2%??

8. Factores que influyen
► Tipo de diseño.
► Tipo de muestreo utilizado.
► Comparación de muestras independientes o
pareadas.

9. Circulo vicioso del cálculo
Cálculo muestral
La frecuencia se Frecuencia del
obtendrá en el estudio Problema en estudio
x
p
r
OR

10. Muestra para la media de población
Población conocida Población no conocida
Las variables son numéricas
El nivel de confianza o seguridad (1-α). El nivel de confianza prefijado da lugar
a un coeficiente (Zα). Para una seguridad del 95% = 1.96; para una seguridad
del 99% = 2.58.
d : error máximo permisible o Tolerancia de error (mayormente 5%)
S2: varianza poblacional

11. Muestra para la media de población
Variables Nominales
siendo
es la varianza de la población.
es la varianza de la muestra, la cual podrá determinarse en
términos de probabilidad como
es error estándar que está dado por la diferencia entre () la media
poblacional y la media muestral.
es el error estándar al cuadrado, que nos servirá para determinar
, por lo que = es la varianza poblacional.

12. Muestra para la media de población
► Ejemplo:
En un área sanitaria, la distribución del peso al nacer de
niños que cumplen su período de gestación de 40 sem. es
aproxim. normal con una media de m=3500 g. y una
DS=430 g.
Un investigador planea llevar a cabo un estudio para
estimar el peso medio al nacer de los niños que llegan al
término del embarazo y cuyas madres fumaron durante
ese período, asumiendo que la DS es la misma. Si el
investigador desea que el error (precisión) sea de 50 g con
una confianza del 95%, ¿qué tamaño de muestra se
requiere en este estudio?

13. Muestra para la proporción de
población
Población conocida Población no conocida
Las variables son nominales
n: Tamaño muestral
N: Tamaño de la población, número total de historias.
Z: Valor correspondiente a la distribución de Gauss 1,96 para α =0,05
p: Prevalencia del fenómeno en estudio.
Q: 1-p
“i” o “d”: Tolerancia de error (mayormente 5%)*.
•Si las prevalencias son bajas, las tolerancias de error lo debe ser aun más.
Ejemplo de la tasa de prevalencia, se puede suponer que la proporción que
ha de estimarse se moverá probablemente entre un 5% y un 15%, y es razonable
aspirar a que no se incurra en un error mayor del 1%.

14. Muestra para la proporción de
población
• Si la seguridad Zα fuese del 90% el coeficiente sería 1.645
• Si la seguridad Zα fuese del 95% el coeficiente sería 1.96
• Si la seguridad Zα fuese del 97.5% el coeficiente sería 2.24
• Si la seguridad Zα fuese del 99% el coeficiente sería 2.576

15. Muestra para la proporción de
población
► Ejemplo: Se quiere calcular la prevalencia de
sujetos con reacciones positivas a la tuberculina
entre los < de 5 años de su circunscripción.
► Calcular cuántos niños han de figurar en una
muestra simple aleatoria para que pueda
estimarse dicha prevalencia con una precisión
absoluta, expresada en %, entre el 3 y el 5% y un
95% de confianza si se cree, por estudios previos,
que la tasa de prevalencia pudiera ser, aproxim.
del 20%.

16. Cálculo del tamaño muestral en
estudios de casos y controles
p2: probabilidad de exposición entre los controles
W: es el OR previsto
P1: la frecuencia de exposición entre los casos,
Así, el problema del cálculo del tamaño muestral podrá abordarse mediante
las fórmulas habituales empleadas en la comparación de dos proporciones,
asumiendo aquí que las proporciones esperadas son p1 y p2

17. Cálculo del tamaño muestral en
estudios de casos y controles
p1: La frecuencia de la exposición entre los casos.
p2: La frecuencia de la exposición entre los controles.
α : La seguridad con la que se desea trabajar, o riesgo de cometer un error de
tipo I. Generalmente se trabaja con una seguridad del 95% (α = 0,05).
1-β: El poder estadístico que se quiere para el estudio, o riesgo de cometer un
error de tipo II. Es habitual tomar β = 0,2, es decir, un poder del 80%.

18. Cálculo del tamaño muestral en
estudios de casos y controles
Donde:
son valores que se obtienen de la distribución normal estándar en función de
la seguridad y el poder elegidos para el estudio. En particular, para una
seguridad de un 95% y un poder estadístico del 80% se tiene que.

19. Cálculo del tamaño muestral en
estudios de casos y controles
n = número de sujetos sin pérdidas
R = proporción esperada de pérdidas

20. Cálculo del tamaño muestral en
estudios de casos y controles
► Ejemplo: Un estudio de casos y controles
emparejado sobre tabaquismo y cáncer de laringe
utilizando controles poblacionales.
► Suponiendo que la prevalencia del hábito
tabáquico en la población es del 45% y que el OR
esperado es aproxim 3
► ¿cuántos pares de casos y controles necesitará
para estimar el OR con una precisión relativa del
15% y un nivel de confianza del 95%?

21. Cálculo del tamaño muestral en
estudios de Cohortes
n : sujetos necesarios en cada una de las muestras
Zα : Valor Z correspondiente al riesgo deseado
Zβ : Valor Z correspondiente al riesgo deseado
S2 : Varianza de la variable cuantitativa que tiene el grupo control o de
referencia.
d : Valor mínimo de la diferencia que se desea detectar (datos cuantitativos).

22. Cálculo del tamaño muestral en
estudios de Cohortes
► Un epidemiólogo proyecta un estudio sobre la posibilidad
de que cierta enfermedad pulmonar esté favorecida por la
exposición a un contaminante atmosférico recién detectado
cuyo efecto no ha sido examinado previamente.
► ¿Qué tamaño tendrá que tener la muestra de cada grupo
(el de expuestos y el de no expuestos) si se desea estimar
el riesgo relativo con una precisión entre el 10% y el 20%
del valor real (el cual, verosímilmente, pudiera ascender a
2) con un 95% de confianza?
► La enfermedad se manifiesta en el 20% de las personas no
expuestas al contaminante atmosférico y los dos grupos
serán de igual tamaño.

23. Los valores Zα según la seguridad y Zβ
más utilizados

24. Tamaño muestral del coeficiente
correlación lineal
Siendo el error estándar de z aproximadamente igual a

25. Tamaño muestral del coeficiente
correlación lineal
A. Planteamiento bilateral B. Planteamiento Unilateral
r: magnitud de la correlación que se desea detectar. Esto se obtiene de
estudios anteriores entre las dos variables a estudio.
1−α: la seguridad con la que se desea trabajar o riesgo de cometer un error
de tipo I. Generalmente se trabaja con una seguridad del 95% (α = 0,05 ).
1−β: el poder estadístico que se quiere para el estudio, o riesgo de cometer
un error de tipo II. Es habitual tomar β = 0,2 o, equivalentemente, un poder
estadístico del 80%.

26. Tamaño muestral del coeficiente
correlación lineal
se obtienen de la distribución normal estándar en función de la seguridad
y el poder elegidos para el estudio. En particular, para una seguridad del
95% y un poder estadístico del 80% se tiene que
A
B

27. Tamaño muestral del coeficiente
correlación lineal
► Supóngase que la correlación entre el volumen
espiratorio forzado en un segundo y la capacidad
vital forzada en individuos sanos es
aproximadamente de 0,60.
► Supóngase, adicionalmente, que un grupo de
pacientes con una enfermedad de pulmón está
accesible en una clínica, e interesa contrastar si
hay correlación entre ambas medidas en esos
pacientes. Con un nivel de confianza del 95% y
una potencia del 90%, ¿cuántos sujetos se
necesitan en la muestra?

28. Ensayos Clínicos
► La formula dependerá del tipo de medida que se este
calculando en el ensayo clinico.
Ejemplo: un ensayo clínico sobre el uso de una droga en
embarazos gemelares, un tocólogo desea demostrar que
hay un aumento significativo en la duración del embarazo
al usar la droga frente a un placebo.
El tocólogo estima que la desviación estándar de la
duración de los embarazos es de 1,75 semanas. ¿Cuántos
embarazos debe observar como mínimo en cada grupo si
considera que una semana es un aumento clínicamente
importante en la duración del embarazo y quiere operar
con una confianza del 95% y una potencia del 80%?

29. Ejercicio 1
► Se desea hacer una encuesta para
determinar la proporción de familias que
carecen de medios económicos para atender
los problemas de salud. Existe la impresión
de que esta proporción está próxima a 0,35.
Se desea determinar un intervalo de
confianza del 95% con un error de
estimación de 0,05. ¿De qué tamaño debe
tomarse la muestra?

30. Ejemplo 2
► Sedesea conocer el peso promedio de
una determinada clase de pescado con
un error de estimación de 0,02 y con
un nivel de confianza del 99%. Por
datos anteriores se sabe que el peso
tiene DS. 4,5. ¿De qué tamaño debe
escoger la muestra? Suponga que los
pesos de estos pescados se distribuyen
normalmente.

31. Ejercicio 3
► Unproductor de semillas desea saber
con un error de estimación del 1% el
porcentaje de semillas que germinan
en la granja de su competidor. ¿Qué
tamaño de muestra debe tomarse para
obtener un nivel de confianza del
95%?

32. Ejercicio
► Enun ensayo clínico sobre el uso de una droga en
embarazos gemelares, un tocólogo desea
demostrar que hay un aumento significativo en la
duración del embarazo al usar la droga frente a un
placebo. El tocólogo estima que la desviación
estándar de la duración de los embarazos es de
1,75 semanas. ¿Cuántos embarazos debe observar
como mínimo en cada grupo si considera que una
semana es un aumento clínicamente importante
en la duración del embarazo y quiere operar con
una confianza del 95% y una potencia del 80%?

33. Ejercicio 4
► Se desea realizar una encuesta entre la
población juvenil de una determinada
localidad para determinar la proporción de
jóvenes que estaría a favor de una nueva
web. El número de jóvenes de dicha
población es N=2.000. Determinar el
tamaño de muestra necesario para estimar
la proporción de estudiantes que están a
favor con un error de estimación de 0.05 y
un nivel de confianza del 95%.

34. Ejercicio 4
► Se desea realizar un estudio de cohortes. Por la
literatura esperamos encontrar un RR en
Expuestos de 1.75, se desea estimar este RR con
su intervalo de confianza. Además sabemos que el
porcentaje de enfermos en población no expuesta
es del 10%.
► Calcular que número de Expuestos y No
Expuestos necesitamos estudiar para tener un
nivel de confianza del 90% asumiendo un error
máximo en el RR del 10%.
► Estudiar como varía este “n” si asumimos un error
máximo del RR del 25%.

35. Ejercicio 5
► Usted desea realizar un estudio de casos y
controles, con 3 controles por caso, para
analizar la influencia del consumo de alcohol
en la aparición de cáncer de esófago.
¿Cuántos sujetos debe estudiar si quiere
poder declarar como significativo un OR de
2,5 o mayor y sabe que la exposición entre
los controles es del 60%? (Suponga un nivel
de confianza del 95% y una potencia del
80%).

36. Ejemplo 5:
Suponiendo un 20% de enfermedad en el grupo de No Expuestos en un
estudio de cohortes, ¿Cuál es el tamaño mínimo que necesitamos en cada
grupo de Expuestos/No Expuestos para estimar el RR en expuestos con un
10% del valor real, pensando que es aproximadamente de 1,75, con un 95%
de confianza?
Con los datos observamos que
P2=0,2
Como RR=(a/n1)/(b/n2); a/n1=p1 y b/n2=p2
Entonces, P1=(RR)P2 = 0,2*1,75 = 0,35
1,962 [(0,65 / 0,35)  (0,8 / 0,2)]
Y N  2026,95
[ln(1  0,1)]2
Si quisiéramos tener un nivel de confianza del 99%
2,5762 [(0,65 / 0,35)  (0,8 / 0,2)]
N  3501,24
[ln(1  0,1)]2

37. Ejemplo 6:
Suponiendo un 15% de enfermedad en el grupo de No Expuestos y una
diferencia máxima del 30% con el grupo de expuestos en un estudio de
cohortes, ¿Cuál es el tamaño mínimo que necesitamos en cada grupo de
Expuesto/No Expuestos para estimar el RR sobre un 20% del valor real, con
un 95% de confianza?
Con los datos observamos que
P1=0,45 1,962 [(0,55 / 0,45)  (0,85 / 0,15)]
N  531,48
P2=0,15 [ln(1  0,2)]2
Si quisiéramos asumir solo un 10% de variabilidad sobre el valor real.
1,962 [(0,60 / 0,40)  (0,85 / 0,15)]
N  2383,99
[ln(1  0,1)]2

38. Ejemplo 8:
Se realiza un estudio multicéntrico para evaluar el efecto de un fármaco sobre
una patología concreta cardiovascular. Los pacientes serán randomizados en
dos Brazos (A y B). Calcular el número de pacientes que debe haber en cada
brazo para un poder del 90% y un nivel de confianza del 95%, con un diseño
de dos colas, asumiendo como peor prevalencia en Brazo B 0,35 y asumiendo
un RR=2.
Con los datos observamos que
P2=0,35 P1=(RR)P2=0.7 P=P1+P2/2=0.525
Sustituyendo en la fórmula
N
1,96 
[2(0,525)(0,475)  1.282 [(0,7)(0,3)  (0,35)(0,65)]
2
 40,67
(0,7  0,35) 2
Si quisiéramos tener un nivel de confianza del 99% y un poder del 80%:
N
2,576 [2(0,525)(0,475)  0,842 [(0,7)(0,3)  (0,35)(0,65)] 
2
 46,09
(0,7  0,35) 2

39. Ejemplo 9:
Aceptando un 15% de enfermedad en el grupo de No Expuestos y una
diferencia máxima del 30% con el grupo de expuestos en un estudio de
cohortes, ¿Cuál es el tamaño mínimo que necesitamos en cada grupo de
Expuesto/No Expuestos para estimar el RR con un error tipo II del 20% y con
un 95% de confianza?
Con los datos observamos que
P1=0,45
P2=0,15
N
1,96 
2
[2(0,525)(0,475)  0,842 [(0,7)(0,3)  (0,35)(0,65)]
 35,44
(0,7  0,35) 2
Si quisiéramos asumir un poder del 90%.
N
1,96 
[2(0,525)(0,475)  1.282 [(0,7)(0,3)  (0,35)(0,65)]
2
 46,94
(0,7  0,35) 2

40. Ejercicio 10
► Alrealizar un protocolo para un estudio de
cohortes, no se encuentra ningún dato sobre el RR
de la enfermedad en expuestos. Se sabe que el %
de enfermos en expuestos es del 20%. Al 95% de
confianza y con un poder del 80%, calcular el
tamaño muestral necesario para estimar el RR
asumiendo como peor:
► a) RR=1.25
► b) RR=2.00
► c) RR=3.00
► d) RR=3.5

41. TIPO DE MUESTREO

43. Muestreo aleatorio simple
► Es aquel en que cada elemento de la
población tiene la misma probabilidad de ser
seleccionado para integrar la muestra.
► Existen dos formas de extraer una muestra
de una población: con reposición y sin
reposición.

44. Muestreo aleatorio simple
► Muestreo con reemplazo: un elemento puede
ser seleccionado más de una vez en la muestra
para ello se extrae un elemento de la población se
observa y se devuelve a la población, por lo que
de esta forma se pueden hacer infinitas
extracciones de la población aun siendo esta finita.
► Muestreo sin reemplazo: No se devuelve los
elementos extraídos a la población hasta que no
se hallan extraídos todos los elementos de la
población que conforman la muestra.

45. Muestreo aleatorio simple
► Ejemplo:
Supóngase que se quiere obtener una MSA
de 120 estudiantes de un centro
universitario que tiene 966 alumnos
registrados.

46. Muestreo sistemático en fases
► También otorga igual probabilidad de
integrar la muestra a todas las unidades de
análisis de la población.
► Se usa para los casos en los que no se
cuenta con una base de datos con el caso
del muestreo aleatorio simple.
► Para su calculo se debe saber el tamaño de
la población y que porcentaje es la muestra
de la población.

47. Muestreo sistemático en fases
► Ejemplo:
Supóngase que se quiere obtener una
muestra sistemática que contenga
aproximadamente al 12% de los estudiantes
de un centro universitario que tiene 966
alumnos registrados.

48. Muestreo aleatorio estratificado
► Un muestreo aleatorio estratificado es aquel
en el que se divide la población de N
individuos, en k sub-poblaciones o estratos,
atendiendo a criterios que puedan ser
importantes en el estudio, de tamaños
respectivos.
N1, . . . , Nk,

49. Muestreo aleatorio estratificado
► Ejemplo:
Supóngase que se quiere obtener una muestra
de 120 estudiantes de un centro universitario
que tiene 966 alumnos registrados, distribuidos
en cuatro áreas académicas con los siguientes
tamaños:
Ingeniería: 264
Ciencias económicas: 284
Ciencias salud: 182
Letras: 236

50. Muestreo por conglomerados
monoetápico
► No se pueda disponer de un listado total de
las unidades de análisis, solo se sabe de
cuantas están conformadas cada unidades
de análisis y/o
► Dispersión geográfica de las unidades de
análisis a lo largo del territorio en que se
halla ubicada la población.

51. Muestreo por conglomerados
monoetápico
► Cuando solo se tienen identificados los
conglomerados y sus tamaños; en este caso
se debe conformar un archivo con tantos
registros como conglomerados, con un
campo que identifique el conglomerado y
otro campo que contenga su tamaño
(número de unidades de que consta).

52. Muestreo por conglomerados
monoetápico
► Ejemplo:
Supóngase que se quiere obtener una
muestra de aproximadamente 120
estudiantes de un centro universitario que
tiene 966 alumnos registrados y que los
alumnos están distribuidos en 52 grupos de
tamaños variables y conocidos.

53. Muestreo por conglomerados
bietápico
► Este procedimiento de selección muestral se
utiliza cuando hay gran variabilidad entre
los tamaños de los conglomerados.
► Se usa para escoger más conglomerados,
claro esta manteniéndose la misma cantidad
de la muestra.

54. Muestreo por conglomerados
bietápico
► Ejemplo:
Supóngase que se quiere obtener una muestra de
120 estudiantes de un centro universitario que
tiene 966 alumnos registrados. Supóngase además
que los alumnos están distribuidos en 52 grupos
de tamaños variables y conocidos y que se ha
decidido seleccionar 12 de esos grupos, o
equivalentemente, 10 alumnos por grupo.

55. Muestreo por conclomerados
bietápico estratificado
► Este procedimiento de selección muestral se
utiliza cuando se quiere aplicar un muestreo
bietápico pero habiendo separado antes las
Unidades de Primera Etapa según estratos.
► Se trata de un método cuyo uso está muy
extendido en la práctica.

56. Muestreo por conclomerados
bietápico estratificado
► Ejemplo:
Supóngase que se quiere obtener una muestra
de 120 estudiantes de un centro universitario
que tiene 966 alumnos registrados. Supóngase
además que hay cuatro áreas académicas y que
en cada una existe cierto número de grupos de
alumnos (14, 14, 11 y 13 grupos
respectivamente) de modo que los alumnos
están distribuidos en 52 grupos de tamaños
variables y conocidos. Considérese, finalmente,
que se ha decidido seleccionar 12 de esos
grupos y 10 alumnos por grupo.