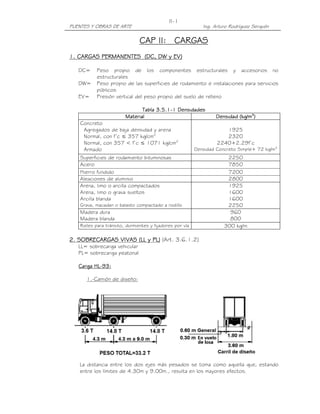
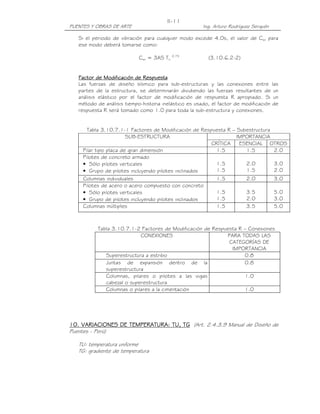
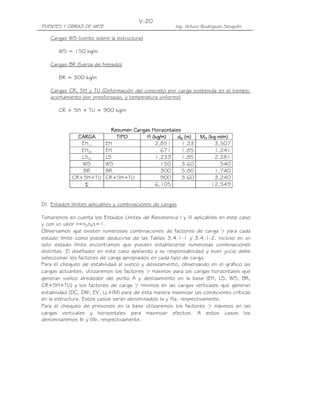
Este documento presenta una introducción a los puentes. Define un puente como una obra que da continuidad a una vía al salvar un obstáculo. Describe las partes principales de un puente, incluyendo la superestructura y la infraestructura. También clasifica los puentes según su función, materiales y tipo de estructura. Explica la importancia de considerar aspectos como la ubicación, estudios básicos e hidráulicos, y geometría al diseñar un puente. Finalmente, resume los elementos geométricos clave de un puente como






















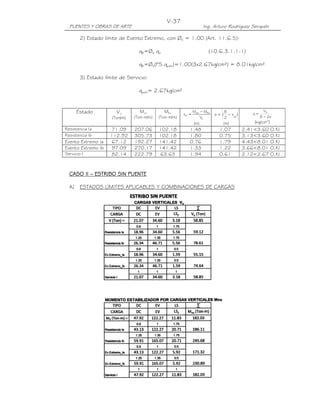
![II-17
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
II-
APÉNDICE II-A
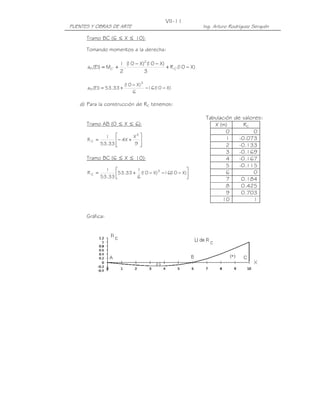
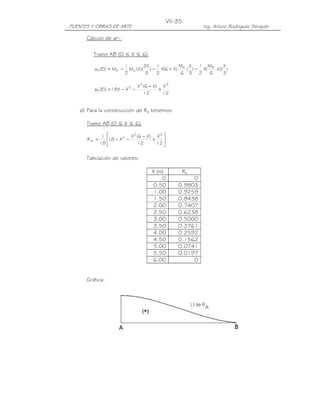
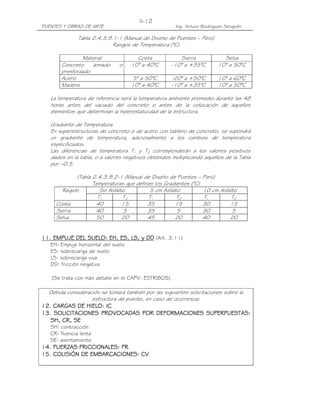
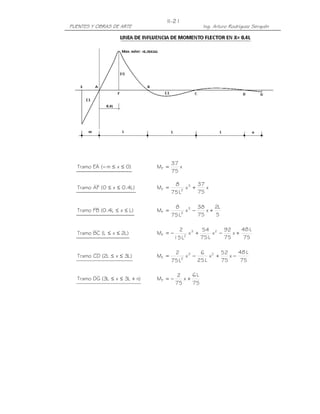
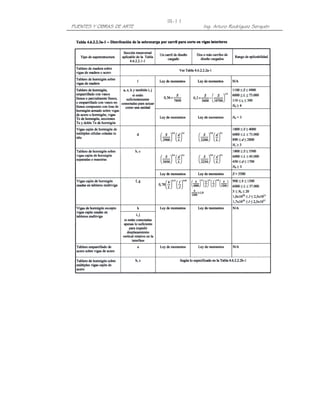
MÁXIMO MOMENTO DE FLEXIÓN EN UNA VIGA SIMPLEMENTE APOYADA PARA UN
TREN DE CARGAS (Teorema de Barré)
Bisecando la distancia entre la resultante de un tren de cargas y la carga más próxima a
ella, por un eje que pasa por el centro de luz, el máximo momento de flexión en una viga
simplemente apoyada se encuentra casi siempre bajo la carga más próxima a la
resultante. En caso de igualdad de distancias, se ubica bajo la carga más pesada.
En efecto, en el tren de cargas mostrado, tomando momentos en el punto donde
incide la carga P3 tenemos:
R= P
P P P P P
1 2 3 4 5
b b
1 2
A B
R R(L-x-e)
= x e (L-x-e)
A L
L
R (L x e)
MP 3 = x P (b1 + b2 )
1 P2b2
L
dMP 3
Para MP 3 = máx, =0
dx
R
[ 1 x) + (L
( x e )] = 0
L
L e
x=
2
Es decir:
L
P P P P P
1 2 3 4 5
b b
1 2
A B
Mmáx R= P
R R(L-x-e)
= x=(L-e)/2 e/2 x=(L-e)/2
A L
e/2
L/2 L/2](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-28-320.jpg)




















![II-45
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
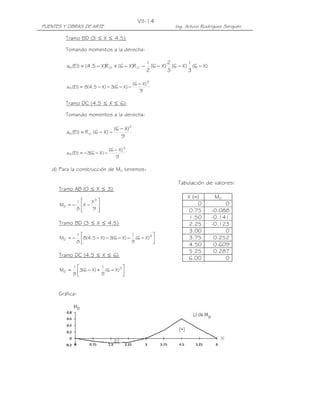
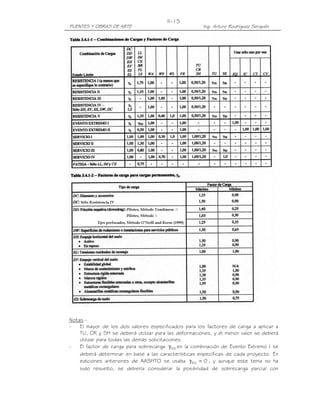
El momento por dos camiones de diseño es:
(-)M2 camiones = 3.6T(-0.880m) + 14.8T(-1.749m-2.048m) +3.6T(-1.593m) +
14.8T(-1.368m-0.709m)
= -95.838 T-m
El momento por la sobrecarga distribuida es:
(-)Ms/c distrib = 0.96 T/m (-46.2 m²) = -44.35 T-m
El momento máximo negativo por sobrecarga, considerando el incremento por
carga dinámica para el estado límite de Resistencia, IM=0.33, es:
(-)Ms/c+IM = 0.90 [(-95.838 T-m ) x 1.33 + (-44.35 T-m)] = -154.63 T-m
T-
NOTA.-
NOTA.
* La utilización del 90 por ciento de la solicitación de dos camiones y la carga de carril
se emplea en el caso de momentos negativos entre puntos de contraflexión debido a
una carga uniforme en todos los tramos (Artículo 3.6.1.3.1). En este caso como se
aprecia en el gráfico, el apoyo interior B se encuentra en el tramo de contraflexión de
9.53m, ámbito para el cual es aplicable lo indicado. Los puntos de contraflexión para
una viga contínua de tres tramos iguales quedan definidos por:
L1 = 0.8L = 16 m , L 2 = 0.4764L = 9.53 m , L 3 = 0.4472L = 8.94 m , con L = 20m.
c) Máximo momento positivo
El máximo momento positivo, después de realizar las combinaciones de carga viva
aplicables, se encuentra posicionando en la línea de influencia el camión de diseño
con un eje posterior en la ordenada máxima, tal como se muestra en la figura. La
sobrecarga distribuida la aplicamos únicamente en el área positiva.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-56-320.jpg)

![II-48
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
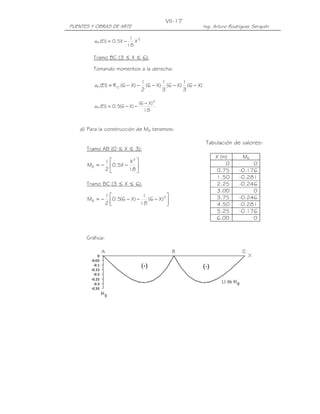
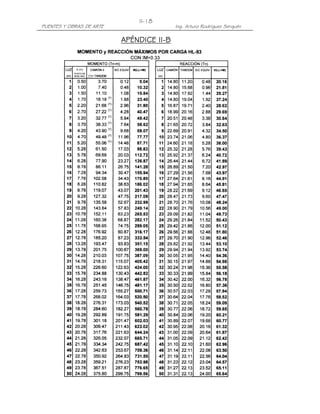
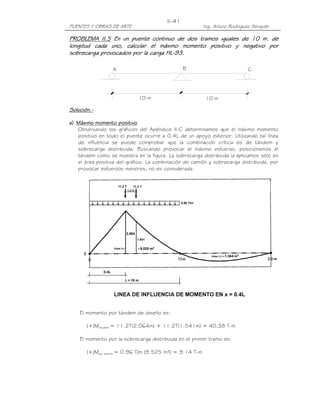
PROBLEMA II.7 Calcular la fuerza de frenado y la fuerza de viento que actúan
II.7
sobre el pilar central del puente mostrado, de dos vías. El viento incide
perpendicularmente al eje longitudinal del puente. Utilizar vehículo HL-93 y
HL-
Especificaciones AASHTO LRFD.
A B C
30 m 30 m
Solución.-
Solución.-
a) Fuerza de Frenado
De acuerdo con las Especificaciones, la fuerza de frenado será la mayor de:
- 25% de los pesos por eje de camión o tandem de diseño
- 5% del camión o tandem de diseño más la carga de carril
En este caso el peso del vehículo HL-93 es 33.2 T, peso del tandem: 22.4 T, carga
de carril: 0.96 T/m.
La fuerza de frenado se calcula con los carriles que transportan tráfico en la misma
dirección. Asumiendo que a futuro los dos carriles transportan tráfico en la misma
dirección y considerando el factor de presencia múltiple m=1.00, tendremos:
BR1 = 0.25 x 33.2 T x 2vías x 1.00 / 1 apoyo = 16.60 T
BR2 = 0.25 x 22.4 T x 2 x 1.00 = 11.20 T
BR3 = 0.05 [33.2 T+(30m + 30m) 0.96 T/m]x2x1.0 = 9.08 T
BR4 = 0.05 [22.4 T+(30m + 30m) 0.96 T/m]x2x1.0 = 8.00 T
Luego, la fuerza de frenado será: 16.60 T, aplicada a 1.80 m sobre la superficie de
calzada.
F = 16.6 T
BR
1.80 m
A B C
30 m 30 m
NOTA.-
NOTA.-
Un vehículo T3S3 circulando por dicho puente a una velocidad de 60 km/h, que al
frenar tarda en detenerse 10 segundos, provocará según las leyes de la física una
fuerza de frenado igual a:
F = m.a](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-59-320.jpg)









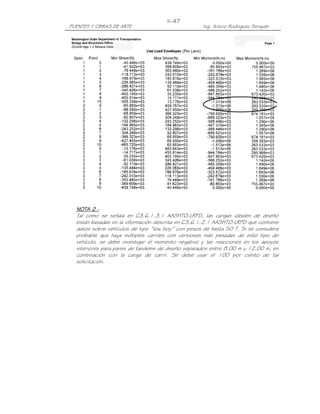
![III-15
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
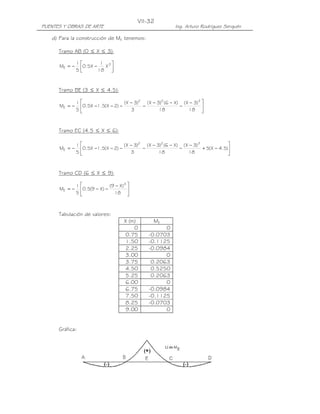
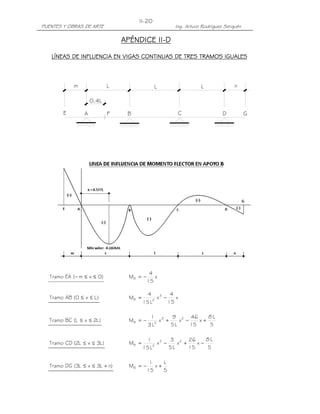
10.
10. LIMITACIÓN DE LA FISURACIÓN MEDIANTE DISTRIBUCIÓN DE LA
ARMADURA (Art. 5.7.3.4)
Todos los elementos de hormigón, excepto losas de tablero diseñadas de
acuerdo con el Art. 9.7.2, deben dimensionarse de manera que en estado límite
de servicio la tensión de tracción en las armaduras de acero no pretensado no sea
mayor que fsa:
Z
fsa = ≤ 0.6fy (5.7.3.4-1)
(d c A )1/ 3
Donde:
dc = altura de hormigón medida desde la fibra extrema comprimida hasta el
centro de la barra o alambre ubicado más próximo a la misma; el espesor
del recubrimiento libre para calcular dc no se deberá tomar mayor que 50
mm.
A = área de hormigón que tiene el mismo baricentro que la armadura principal
de tracción y limitada por las superficies de la sección transversal y una
recta paralela al eje neutro , dividida por el número de barras o alambres;
el espesor del recubrimiento libre para calcular A no se deberá tomar
mayor que 50 mm.
Z = parámetro relacionado con el ancho de fisura
≤ 30,000 N/mm para elementos en condiciones de exposición moderada
≤ 23,000 N/mm para elementos en condiciones de exposición severa
≤ 17,500 N/mm para estructuras enterradas
≤ 23,000 N/mm para el diseño transversal de las vigas cajón de hormigón
por segmentos para cualquier carga aplicada antes que el hormigón alcance
la totalidad de su resistencia nominal.
Para alcantarillas de sección rectangular voladas in situ, el valor de Z no
deberá satisfacer la condición Z ≤ 27000 / β , siendo β = [1+ dc / 0.7d]
d = distancia entre la cara comprimida y el baricentro de la armadura de tracción
Si en el estado límite de servicio las alas de las vigas Te o vigas cajón están
traccionadas, la armadura de tracción por flexión se deberá distribuir en una
distancia igual al menor de: el ancho de ala efectivo (Art. 4.6.2.6) o un ancho igual
a 1/10 del promedio de los tramos adyacentes entre apoyos.
Si el ancho de ala efectivo es mayor que 1/10 de la longitud del tramo, en las
porciones exteriores del ala se deberá disponer armadura longitudinal adicional con
un área no menor que 0.4% del área de losa en exceso.
Si la profundida efectiva de de un elemento de hormigón no pretensado o
parcialmente pretensado es mayor que 90 cm, se deberá distribuir uniformemente
armadura superficial en ambas caras del elemento en una distancia d/2 más próxima
de la armadura de tracción por flexión. En cada cara lateral el área de armadura
superficial Ask, en mm2/mm de altura, deberá satisfacer la siguiente condición:
Armadura de contracción y temperatura en caras laterales (Art. 5.10.8)
A s + A ps
A sk ≥ 0.001(d e − 760) ≤ (5.7.3.4-4)
1200](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-77-320.jpg)









![III-25
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
r
ff ≤ 1479 − 0.33fmin + 561( ) en kg/cm² (5.5.3.2-1)
h
Donde:
ff = rango de tensión
fmin = mínima tensión por sobrecarga resultante de la combinación de cargas
correspondiente a la fatiga, combinada con la tensión más severa debida ya
sea a las cargas permanentes o a las cargas permanentes más las cargas
externas inducidas por contracción y fluencia lenta; la tracción se considera
positiva, la compresión negativa
r/h = relación entre el radio de base y la altura de las deformaciones
transversales; si se desconoce el valor real se puede utilizar r/h = 0.3
En losas de tablero de hormigón en aplicaciones multiviga no es necesario
investigar la fatiga.
18. BARRERAS DE CONCRETO
El propósito de una barrera de concreto en el caso de una colisión vehicular es
redirigir el vehículo de una manera controlada. La barrera debe ser adecuada para
resistir el impacto inicial de la colisión y seguir siendo eficaz en la reorientación
del vehículo, debiendo por ello cumplir requisitos de resistencia y geometría.
Secciones de barreras junto a cuantías de acero que pueden controlar colisiones
se han desarrollado a lo largo de los años y se ha demostrado su eficacia por
pruebas de choque.
Los requisitos de resistencia dependen del volumen de camiones y la velocidad
del tráfico previsto. Las fuerzas de diseño y su ubicación en relación con la losa
de puente están dadas en seis niveles según la Tabla AASHTO A13.2-1.
Cabe destacar que un sistema de barreras y su conexión a la cubierta sólo se
autoriza después de demostrar que es satisfactorio a través de pruebas de
choque en barreras a escala natural para el nivel de prueba deseado [A13.7.3.1].
Si se realizan modificaciones menores a modelos ya probados, que no afectan su
resistencia, pueden utilizarse sin las pruebas de impacto requeridas. Así mismo es
importante detallar el acero que se extiende de la barrera a la losa y analizar la
resistencia del voladizo para la transferencia de la carga de choque.
Número de lados aptos para el impacto
En función de su número de lados, las barreras se clasifican en simples y
dobles. Las simples tienen una sección transversal que presenta un solo
lado apto para el impacto. Las dobles, en cambio, cuentan una sección
transversal con ambos lados aptos para el impacto.
La barrera simple es un elemento longitudinal y asimétrico que se utiliza
como barrera lateral, al lado derecho de la calzada o en pares opuestos
como separador central. Se ubica a los lados de una vía frente a
terraplenes, depresiones o estructuras que signifiquen posibilidad de
colisión. Sirven también como protección de los muros de contención,
revestimiento de túneles y barandas de puentes.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-87-320.jpg)






![III-33
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
donde:
Rw= resistencia del parapeto especificada en el Artículo A13.3.1 (N)
Lc = longitud crítica del patrón de falla por líneas de fluencia (mm)
H = altura del muro (mm)
T = fuerza de tracción por unidad de longitud del tablero (N/mm)
El diseño del vuelo del tablero para las fuerzas verticales especificadas en
el Caso de Diseño 2 se deberá basar en la porción del tablero en voladizo.
Transferencia de Corte en las Interfases − Corte por Fricción (Art. 5.8.4)
Se debe considerar la transferencia de corte en la interfase en un plano
dado por: una fisura existente o potencial, una interfase entre diferentes
materiales, o una interfase entre dos hormigones colados en diferentes
momentos.
La resistencia nominal al corte del plano de interfase se debe tomar como:
[
Vn = cA cv + µ A vf fy + Pc ] (5.8.4.1-1)
La resistencia nominal al corte utilizada en el diseño no deberá ser mayor
que el menor valor entre los siguientes:
'
Vn ≤ 0.2fc A cv (5.8.4.1-2)
ó bien
Vn ≤ 5.5A cv (5.8.4.1-3)
donde:
Vn = resistencia nominal al corte (N)
Acv = área del hormigón que participa de la transferencia de corte (mm2)
Avf = área de la armadura de corte que atraviesa el plano de corte (mm2)
fy = tensión de fluencia de la armadura (MPa)
c = factor de cohesión especificado en el Artículo 5.8.4.2 (MPa)
µ = coeficiente de fricción especificado en el Artículo 5.8.4.2
Pc = fuerza de compresión permanente neta normal al plano de corte; si la
fuerza es de tracción Pc = 0,0 (N)
f'c = resistencia especificada del hormigón más débil a 28 días (MPa)
La armadura para el corte en las interfases entre hormigones de losas y
vigas puede consistir en barras individuales, estribos de múltiples ramas o
las ramas verticales de una malla de alambre soldada. El área de la sección
transversal Avf de la armadura por unidad de longitud de viga debería
satisfacer ya sea el área requerida por la Ecuación 1 o bien:](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-95-320.jpg)




![III-38
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
B.2) Resumen de momentos flectores y criterios LRFD aplicables (Tabla 3.4.1-1)
MOMENTOS POSITIVOS POR CARGAS (FRANJA INTERIOR)
Carga M(+) T-m
T- γ
Resistencia I Servicio I Fatiga
DC 8.64 1.25 1.0 0
DW 0.90 1.50 1.0 0
LL+IM 19.03 1.75 1.0 0.75
Resistencia I: U = n[1.25DC+1.50DW+1.75(LL+IM)]
Servicio I: U = n[1.0DC+1.0DW+1.0(LL+IM)]
Fatiga: U = n[0.75(LL+IM)]
B.3) Cálculo del Acero
Para el Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(8.64) + 1.50(0.90) + 1.75(19.03) = 45.45 T-m
As principal paralelo al tráfico
Utilizando As ∅1” y recubrimiento r= 2.5cm (Tabla 5.12.3-1)
2.54
z = 2.5 + = 3.77 cm d
2 0.45 m
d= 45cm – 3.77cm = 41.23cm z
Mu 45.45x 5
10
As = = = 30.98 cm2
a a
0.9fy (d ) 0.9x4200(41.23 - )
2 2
Asx4200
a= = 0.157 As = 4.86 cm
0.85x315x
100
5.10
La separación será: s = = 0.16 m
30.98
USAR 1∅1” @ 0.16m
0.16
As máximo (Art. 5.7.3.3.1)
Una sección no sobre reforzada cumple con: c /de ≤ 0.42
f ' − 280
Como β1 = 0.85 − 0.05 c ' 2
70 para fc > 280 kg / cm , β1 = 0.825
c = a / β1 = 4.86 / 0.825 = 5.89 cm
de = 41.23 cm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-100-320.jpg)
![III-39
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
c /de = 0.14 ≤ 0.42 OK!
As mínimo (Art. 5.7.3.3.2)
La cantidad de acero proporcionado debe ser capaz de resistir el menor valor
de1.2Mcr y 1.33Mu:
a) 1.2Mcr = 1.2fr S = 1.2(35.67 kg/cm2)(33,750 cm3) = 14.45 T-m
Siendo:
fr = 0.63 fc MPa = 2.01 fc kg / cm2 = 2.01 315 = 35.67 kg / cm2
' '
S = bh2/6 = 100(45)2/6 = 33,750 cm3
b) 1.33 Mu= 1.33(45.45 T-m) = 60.45 T-m
El menor valor es 14.45 T-m y la cantidad de acero calculada (30.98 cm2)
resiste Mu=45.45 T-m > 14.45 T-m OK!
As de distribución
1750
%= ≤ 50% (Art. 9.7.3.2)
S
1750
%= =19.57%
8000
As repart = 0.1957(30.98 cm2) = 6.06 cm2
2
Utilizando varillas ∅5/8”, la separación será: s = = 0.33m
6.06
USAR 1∅5/8” @ 0.33 m
As de temperatura
Ag
A s temp = 0.756 [SI] (5.10.8.2-1)
Fy
A s temp = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ]
100) = 8.1cm2
A s temp = 0.0018(45x
A s temp = 8.1cm2 / 2 = 4.05 cm2 / capa
1.29
Utilizando varillas ∅1/2”, la separación será: s = = 0.32m
4.05
smáx = 3t = 3(0.45)= 1.35m (Art.5.10.8)
smáx = 0.45m OK! (Art.5.10.8)
USAR 1∅1/2” @ 0.32 m
0.32](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-101-320.jpg)



![III-43
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Carga viva (LL):
Para una línea de ruedas de tándem (crítico) y una porción tributaria de la carga
de vía de 3.00m de ancho, de la Tabla APÉNDICE II-B con la consideración de
carga dinámica (33%) en estado límite de Resistencia I:
0.30m + 0.77m
MLL +IM = 0.5 x 38.33Tm x1.33 + 7.64Tm /1.47m
3.00m
MLL+IM = 19.19 T-m
C.3) Resumen de momentos flectores y criterios LRFD aplicables (Tabla 3.4.1-1)
MOMENTOS POSITIVOS POR CARGAS (FRANJA DE BORDE)
Carga M(+) T-m
T- γ
Resistencia I Servicio I Fatiga
DC 11.92 1.25 1.0 0
DW 0.66 1.50 1.0 0
LL+IM 19.19 1.75 1.0 0.75
Resistencia I: U = n[1.25DC+1.50DW+1.75(LL+IM)]
Servicio I: U = n[1.0DC+1.0DW+1.0(LL+IM)]
Fatiga: U = n[0.75(LL+IM)]
C.4) Cálculo del Acero
Para el Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(11.92Tm) + 1.50(0.66Tm) + 1.75(19.19Tm) = 49.47 T-m
As principal paralelo al tráfico
Utilizando As ∅1” y recubrimiento r= 2.5cm (Tabla 5.12.3-1)
2.54
z = 2.5 + = 3.77 cm d
2 0.45 m
d= 45cm – 3.77cm = 41.23cm z
Mu 49.47x 5
10
As = = = 33.94cm2
a a
0.9fy (d ) 0.9x4200(41.23 - )
2 2
Asx4200
a= = 0.157As = 5.33cm
0.85x315x
100](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-105-320.jpg)







![III-51
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
• Aunque el acero principal es perpendicular al tráfico es posible tomar
como en versiones anteriores del AASHTO, la expresión:
S + 3000
t min = ≥ 165 mm (Tabla 2.5.2.6.3-1)
30
1800 + 3000
t min = = 160mm ≥ 165mm
30
tmín= 0.165m
Siendo:
S = luz libre de losa = 1800mm
• En voladizos de concreto que soportan barreras de concreto, el
espesor mínimo de losa es:
tmín= 0.20m (Art. 13.7.3.1.2)
• Teniendo en cuenta las disposiciones sobre el espesor de la losa
uniformizamos con t = 0.20m
0.20m.
B) Criterios LRFD aplicables (Tabla 3.4.1-1)
Resistencia I: U = n[(1.25 ó 0.9)DC+(1.50 ó 0.65)DW+1.75(LL+IM)]
Servicio I: U = n[1.0DC+1.0DW+1.0(LL+IM)]
Conforme al Art. 9.5.3, no es necesario investigar el estado de fatiga en tableros
de concreto en vigas múltiples.
C) Momentos de flexión por cargas
3.60 3.60
_ _
x=.13 x=.13
P S=2% S=2% P
barrera Asfalto 2" barrera
t
Cartelas 9"x6"
.15 Diafragma
.375 .15 b b=.25
.30 .15
0.825 L=2.10 2.10 2.10 0.825
0.4L
E A F B C D G](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-113-320.jpg)


![III-54
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
4
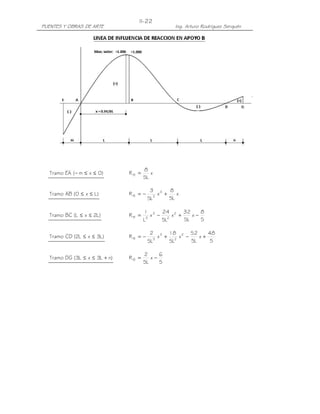
Tramo EA (−0.825 m ≤ x ≤ 0) MB = − x
15
80 3 4
Tramo AB (0 ≤ x ≤ 2.10 m) MB = x − x
1323 15
100 3 6 2 46 84
Tramo BC (2.10 m ≤ x ≤ 4.20 m) MB = − x + x − x+
1323 7 15 25
20 3 6 2 26 84
Tramo CD (4.20 m ≤ x ≤ 6.30 m) MB = x − x + x−
1323 21 15 25
x 21
Tramo DG (6.30 m ≤ x ≤ 7.125 m) MB = − +
15 50
Para un carril cargado, y afectado del factor de presencia múltiple m (Art.
3.6.1.1.2):
M(-) = [7.4T(-0.215m)+7.4T(-0.164m)]1.2= -2.80 Tm x 1.2 = -3.36T-m
Para dos carriles cargados:
M(-)=[7.4T(-0.215m)+7.4T(-0.164m)+7.4(+0.008m)+7.4(0.016m)]1.0
= -2.63 Tm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-116-320.jpg)



![III-58
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Resultados:
M(-
M(-)LL+IM en B, unidades: T-m
T-
COMPARACIÓN M( - )LL+IM, izq M( - )LL+IM, eje B M( - )LL+IM, der
MÉTODO A -1.75 -2.54 -1.86
MÉTODO B -2.00 -2.73 -2.00
MÉTODO C -2.19 -2.55 -2.19
Optaremos por la solución que ofrece el Método A, aunque es posible optar por
cualquiera de los otros métodos. Observar que los resultados del Método C son
una aproximación a lo encontrado con detalle por el Método A y que el Método B
siendo más conservador, simplifica considerablemente el proceso de diseño.
RESUMEN DE MOMENTOS NEGATIVOS POR CARGAS EN B
Carga Tipo M(-) izq M(-) eje M(-) der γ(Resistencia I)
T-m T-m T-m
Losa DC1 -0.12 -0.18 -0.12 1.25
Barrera DC2 +0.04 +0.07 +0.07 0.9
Asfalto DW -0.03 -0.04 -0.03 1.5
Carga viva LL+IM -1.75 -2.54 -1.86 1.75
Para el Diseño por Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[(1.25 ó 0.9)MDC+(1.50 ó 0.65)MDW+1.75M(LL+IM)] (Tabla 3.4.1-1)
En el eje B:
Mu = 1.25(-0.18)+0.9(0.07)+1.50(-0.05)+1.75(-2.54)= -4.68 T-m
En cara de viga izquierda:
Mu = 1.25(-0.12)+0.9(0.04)+1.50(-0.03)+1.75(-1.75)= -3.22 T-m
En cara de viga derecha:
Mu = 1.25(-0.12)+0.9(0.07)+1.50(-0.03)+1.75(-1.86)= -3.39 T-m
El acero negativo será diseñado con este último valor de momento que es el
mayor de las dos caras de viga.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-120-320.jpg)

![III-60
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
efecto
3. Carga Viva y efecto de Carga Dinámica (LL+IM):
MÉTODO A: Proceso analítico
Para un carril cargado, y con el factor de presencia múltiple m (Art. 3.6.1.1.2):
M(+)= [7.4T(0.429m)+7.4T(-0.061m)]1.2= 2.723T-m x 1.2=3.27 T-m
Para dos carriles cargados:
M(+)=[7.4T(0.429m)+7.4T(-0.061m)+7.4(0.007m)+7.4(0.004)]1.0
= 2.80 T-m
El ancho de franja en que se distribuye es:
E(+)= 660+0.55 S’ (Tabla 4.6.2.1.3-1)
= 660+0.55(2100)= 1815 mm = 1.82 m
Entonces, el momento positivo crítico considerando el efecto de carga
dinámica (33% para el Estado Límite de Resistencia) y el ancho de franja, es:
3.27
M(+)LL+IM= x1.33 = 2.39 Tm
1.82](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-122-320.jpg)
![III-61
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
A4-
MÉTODO B: Uso de la Tabla A4-1(AASHTO LRFD)
Para S= 2.10 m:
N mm T−m
M(+)LL+IM= 23380 = 2.38
mm m
III-
MÉTODO C: De momentos corregidos (Ver Apéndice III-A)
Para un carril cargado:
Usando la línea de influencia de momento flector en x=0.4L, y la Ecuación 1
del Apéndice III-A, se puede reducir el momento para el eje vehicular que
coincide con la ordenada máxima (en x = 0.4L) extendiendo la carga de
rueda en un ancho de 0.51m más el grosor de la losa (Art. 4.6.2.1.6) con:
PB P
ML = MOL − (Ecuación 1, Apéndice III-A)
8
Donde:
ML = momento positivo de diseño ajustado por carga viva para un eje
MOL= momento positivo usando cargas de rueda concentradas
= 7.4T(0.429) = 3.17 T-m
P = carga de rueda concentrada en el punto de interés
= 7.4T
BP = longitud de base de la carga de rueda extendida (0.51m más el
peralte de la losa)
= 0.51m + 0.20m = 0.71m
7.4T(0.71m)
ML = 3.17 Tm − =2.51T-m
8
Para el otro eje vehicular la modificación es despreciable, por lo que
incluyendo el factor de presencia múltiple m (Art. 3.6.1.1.2) se tendrá:
M(+)= [2.51Tm+7.4T(-0.061m)]1.2= 2.47T-m
Para dos carriles cargados:
M(+)= [2.51Tm+7.4T(-0.061m)+7.4T(0.007m)+7.4T(0.004)]1.0
= 2.14 T-m
Entonces el momento positivo crítico, afectado del efecto de carga dinámica
(33% para el Estado Límite de Resistencia) y el ancho de franja, es:
2.47
M(+)LL+IM= x1.33 = 1.81 T − m
1.82](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-123-320.jpg)
![III-62
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Resultados:
M(+
M(+)LL+IM en F, unidades: T-m
T-
COMPARACIÓN M(+)LL+IM
MÉTODO A +2.39
MÉTODO B +2.38
MÉTODO C +1.81
Optaremos en este caso conservadoramente por los resultados del Método A.
Notar que el Método C en este caso logra menores valores al tratar las cargas de
eje como cargas extendidas antes que puntuales, situación permitida por el
Reglamento AASHTO (Art. 4.6.2.1.6).
RESUMEN DE MOMENTOS POSITIVOS POR CARGAS EN F
Carga Tipo M(+) T-m γ(Resistencia I)
Losa DC1 0.08 1.25
Barrera DC2 -0.18 0.9
Asfalto DW 0.03 1.5
Carga viva LL+IM 2.39 1.75
Para el Diseño por Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[(1.25 ó 0.9)MDC+(1.50 ó 0.65)MDW+1.75M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(0.08)+0.9(-0.18)+1.50(0.03)+1.75(2.39)= +4.17 T-m
D) Cálculo del Acero
D.1) Acero Negativo (perpendicular al tráfico)
Mu =-3.39 T-m
Utilizando As ∅ ½” y recubrimiento r= 5.0 cm (Tabla 5.12.3-1)
1.27
z = 5.0 + = 5.64 cm
2 z
d 0.20 m
d= 20cm – 5.64cm = 14.36cm
3.39x 5
10
A s ( −) = = 6.50 cm2
a
0.9x4200( .36 − )
14
2
Asx4200
a= = 1.14 cm
0.85x280x
100
1.29
Utilizando varillas ∅1/2”, la separación será: s = = 0.20 m
6.50
USAR 1∅1/2” @ 0.20m
As máximo (Art. 5.7.3.3.1)
Una sección no sobre reforzada cumple con: c /de ≤ 0.42](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-124-320.jpg)

![III-64
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Como:
c = a / β1 = 1.19 / 0.85 = 1.40 cm
de = 16.86 cm
c /de = 0.08 ≤ 0.42 OK!
As mínimo (Art. 5.7.3.3.2)
La cantidad de acero proporcionado debe ser capaz de resistir el menor valor
de1.2Mcr y 1.33Mu:
a) 1.2Mcr = 1.2(fr S) = 1.2(33.63 kg/cm2)(6,667 cm3) = 2.69 T-m
Siendo:
fr = 0.63 fc MPa = 2.01 fc kg / cm2 = 2.01 280 = 33.63 kg / cm2
' '
S = bh /6 = 100(20) /6 = 6,667 cm3
2 2
b) 1.33 Mu= 1.33(4.17T-m) = 5.55T-m
El menor valor es 2.69T-m y la cantidad de acero calculada (6.78cm2)
resiste:
Mu=4.17T-m > 2.69T-m OK!
D.3) As de temperatura
Ag
A s temp = 0.756 [SI] (5.10.8.2-1)
Fy
A s temp = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ]
100 = 3.60 cm2
A s temp = 0.0018x20x
3.60 cm2
En dos capas se colocará: = 1.80 cm2 / capa
2
0.71
Utilizando varillas ∅3/8”, la separación será: s = = 0.39 m
1.80
smáx = 3t = 3(0.20)= 0.60m (Art.5.10.8)
smáx = 0.45m (Art.5.10.8)
USAR 1∅3/8” @ 0.39 m
Nota.- El acero de temperatura se colocará, por no contar con ningún tipo de
acero, en la parte superior de la losa, en el sentido del tráfico.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-126-320.jpg)

![III-66
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Ø 1Ø1/2"@0.20
d c = recubrimie4 +
14 24nto 2
4 3
≤ 5 cm ( Art.5.7.3.4 ) dc
dc
1.27
d c = 5 cm + cm 20 cm
2
dc = 5.64cm
b = espac. del acero = 20cm
20 cm
nv = número de varillas = 1
(2d c )b (2x5.64cm)(20cm)
A = = = 225.60 cm2 (Art. 5.7.3.4)
nv 1
Z = 30,000 N/mm (condición de exposición moderada) (Art. 5.7.3.4)
= 30,591 Kg/cm
Luego:
30,591kg / cm
fsa = = 2, 823 kg / cm2
(5.64cm x 225.60cm2 )1 / 3
fsa ≤ 0.6(4200kg / cm2 ) = 2,520 kg / cm2
fsa = 2,520 kg / cm2
Esfuerzo del acero bajo cargas de servicio
Ms c
fs = n
I
Para el Diseño por Estado Límite de Servicio I, con n= nDnRnI=1:
Ms = n ( .0 MDC +1.0 MDW +1.0 MLL +IM )
1 (Tabla 3.4.1-1)
Ms = 1.0[1.0x(-0.12+0.07)+1.0x(-0.03)+1.0x(-1.86)]
Ms = -1.94 T-m, para un metro de franja.
Luego:
Ms = (-1.94T-m/m) (0.20m) =-0.39T-m
Es =200,000 MPa = 2’039,400 kg/cm2 (5.4.3.2)
'
E c = 15,344 f c (5.4.2.4-1)
E c = 15,344 280 = 256, 754 kg / cm2
E s 2'039,400 kg / cm2
n= = =8
Ec 256,754 kg / cm2](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-128-320.jpg)

![III-68
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
b = espac. del acero = 19cm
nv = número de varillas = 1
(2d c )b (2x3.14cm)( cm)
19
A= = = 119.32 cm2 (Art. 5.7.3.4)
nv 1
Z = 30,000 N/mm (condición de exposición moderada) (Art. 5.7.3.4)
= 30,591 Kg/cm
30,591kg / cm
Luego: fsa = = 4, 243 kg / cm2
(3.14cm x 119.32cm2 )1/ 3
fsa ≤ 0.6(4200kg / cm2 ) = 2,520 kg / cm2
fsa = 2,520 kg / cm2
Esfuerzo del acero bajo cargas de servicio
Ms c
fs = n
I
Para el Diseño por Estado Límite de Servicio I, con n= nDnRnI=1:
Ms = n ( .0 MDC +1.0 MDW +1.0 MLL +IM )
1 (Tabla 3.4.1-1)
Ms = 1.0[1.0x(0.08-0.18)+1.0x(0.03)+1.0x(2.39)]
Ms = 2.32T-m, para un metro de franja.
Luego:
Ms = (2.32T-m/m) (0.19m) =0.44T-m
Es =200,000 MPa = 2’039,400 kg/cm2 (5.4.3.2)
E c = 15,344 fc' (5.4.2.4-1)
E c = 15,344 280 = 256, 754 kg / cm2
E s 2'039,400 kg / cm2
n= = =8
Ec 256,754 kg / cm2](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-130-320.jpg)


![III-71
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
El % de momento g que se distribuye a una viga interior es:
Caso de un carril cargado:
0.1
Kg
0.4 0.3
S S 3
g = 0.06 + Lt (Tabla 4.6.2.2.2b-1)
4300 L s
0.1
Kg
Cálculo de 3
Lt :
s 2.10 m
E viga
n= = 1.0 c .20
E losa
e=0.425
g
30(65) 3 .65 0.85
Iviga = = 686, 563 cm 4
12
A viga = 30(65) = 1950 cm2
e g = 42.5 cm 0.30
K g = n (Iviga + A viga e 2 ) = 1[686, 563 +1950(42.5)2 ] = 4'208, 751 cm 4
g
0.1 0.1
Kg 4'208, 75 cm 4
1
Luego: = = 0.921
Lt 3 1200cm ( 20 cm) 3
s
0.4 0.3
2100 2100
g = 0.06 + ( 0.921) = 0.470
4300 12000
Caso de dos carriles cargados:
0.1
Kg
0.6 0.2
S S 3
g = 0.075 + Lt (Tabla 4.6.2.2b-1)
2900 L s
0.6 0.2
2100 2100
g = 0.075 + (0.921) = 0.611 (CRÍTICO)
2900 12000
MLL+IM= 0.611(98.83 T-m) = 60.39 T-m
C) Resumen de momentos flectores y criterios LRFD aplicables (Tabla 3.4.1-1)
RESUMEN DE MOMENTOS POSITIVOS POR CARGAS
Carga M(+) T-m
T- γ
Resistencia I Servicio I Fatiga
DC 29.68 1.25 1.0 0
DW 4.25 1.50 1.0 0
LL+IM 60.39 1.75 1.0 0.75
Resistencia I: U = n[1.25DC+1.50DW+1.75(LL+IM)]
Servicio I: U = n[1.0DC+1.0DW+1.0(LL+IM)]
Fatiga: U = n[0.75(LL+IM)]](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-133-320.jpg)
![III-72
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
D) Cálculo del Acero Principal (Diseño como viga T, ver APÉNDICE III-A)
Para el Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(29.68) + 1.50(4.25) + 1.75(60.39) = 149.16 T-m
Según el procedimiento de diseño para vigas T señalado en el Apéndice III-B, se
tiene:
Ancho efectivo de viga T (Art. 4.6.2.6), el menor valor de:
L/4= 12/4 = 3.00m
12tf+ tw= 12(0.20)+0.30= 2.70m
S= 2.10m
b=2.10 m
c .20
Luego b= 2.10m
h= 0.85
Suponiendo c= t= 0.20m
z
a= 0.85c= 0.85(20)= 17cm b=0.30
Utilizando As=12∅1” con la distribución mostrada, estribos ∅ 1/2” y
recubrimiento r= 5.0 cm (2”) (Tabla 5.12.3-1)
0.5"
1.5" 3.5"
1.0"
z 1.0"
0.5" 3.5"
2"
2" 2"
0.30 m
Cálculo de “z” :
Tomando momentos en la base de la viga, siendo A=5.10 cm2:
(12A) z = (4A)(3.5”)+(4A)(7”)+(2A)(3”)+(2A)(6.5”)
z= 5.083” =12.91 cm
d= 85cm – 12.91cm = 72cm
Mu 149.16x 5
10
As = = = 62.14 cm2
a 0.9x4200(72 −
17
)
0.9fy (d ) 2
2
As 62.14
ρ= = = 0.00411
bd 210(72)](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-134-320.jpg)
![III-73
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
ρfy d 1.18x0.00411 4200x72
x
c = 1.18 = = 6.16 cm < 20cm
0.85fc' 0.85x280
∴ Se diseñará como viga rectangular
149.16x 5
10
As = = 56.68 cm2 (Con 12∅1” As=61.2cm2)
a
0.9x4200(72 − )
2
Asx4200
a= = 4.76 cm
0.85x280x210
As máximo (Art. 5.7.3.3.1)
Una sección no sobre reforzada cumple con: c /de ≤ 0.42
Como:
c = a / β1 = 4.76 / 0.85 = 5.60 cm
de = 72 cm
c /de = 0.08 < 0.42 OK!
As mínimo (Art. 5.7.3.3.2)
La cantidad de acero proporcionado debe ser capaz de resistir el menor valor
de1.2Mcr y 1.33Mu:
a) 1.2Mcr = 1.2fr S = 1.2(33.63 kg/cm2)(252,875cm3) = 102.05T-m
Siendo:
fr = 0.63 fc' MPa = 2.01 fc' kg / cm2 = 2.01 280 kg / cm2 = 33.63 kg / cm2
S = bh2/6 = 210(85)2/6 = 252,875cm3
b) 1.33 Mu= 1.33(149.16T-m) = 198.38T-m
El menor valor es 102.05T-m y la cantidad de acero calculada (56.68cm2)
resiste Mu=149.16T-m > 102.05T-m OK!
USAR 12∅1”
Armadura de contracción y temperatura en caras laterales (Art. 5.10.8)
En el alma de la viga T:
Ag
A s temp = 0.756 [SI] (5.10.8.2-1)
Fy
A s temp = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ]
A s temp = 0.0018x30 x( 85 − 20) = 3.51cm2](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-135-320.jpg)






![III-80
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Distribución en viga interior:
Caso de un carril cargado:
S
g = 0.36 + (Tabla 4.6.2.2.3a-1)
7600
2100
g = 0.36 + = 0.636
7600
Caso de dos carriles cargados:
2
S S
g = 0.2 + − (Tabla 4.6.2.2.3a-1)
3600 10700
2
2100 2100
g = 0.2 + − = 0.745 (CRÍTICO)
3600 10700
VLL+IM= 0.745(35.66T) = 26.57T= 26.570kg
Para el Diseño por Estado Límite de Resistencia I, con n= nDnRnI=1:
Vu = n[1.25 VDC + 1.50 VDW + 1.75 V(LL+IM)] (Tabla 3.4.1-1)
Vu = 1.25(8,346)+1.50(1,222)+1.75(26,570) = 58,763kg
Cortante actuante : Vu = 58,763kg
Cortante resistente : Vr = Ø Vn (5.8.2.1-2)
Ø = 0.9 (5.5.4.2)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdv + Vp (5.8.3.3-2)
Donde:
Cortante resistente concreto Vc = 0.083β fc' b v d v [N] (5.8.3.3-3)
'
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc b v d v [kg]
A v fy d v (cot θ + cot α )senα
Cortante resistente acero: Vs = (5.8.3.3-4)
s
con ᒕ = 45° (Art. 5.8.3.4) A v fy d v
α = 90° (ángulo de inclinación del estribo) Vs =
s
Cortante resistente concreto (Vc)
' '
Vc = 0.083β fc b v d v [N] = 0.53 fc b v d v [kg] = 0.53 280 (30 x69.62)
Vc = 18,523kg
siendo bv = ancho del alma= 30 cm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-142-320.jpg)
![III-81
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Cortante resistente del acero (Vs)
Se propone estribos Ø1/2” espaciados cada 15 cm. Luego:
A v fy d v (cot θ + cot α)senα A v fy d v 2.58(4200)(69.62)
Vs = = = = 50, 293 kg
s s 15.0
donde:
s = 15.0 cm (espaciamiento asumido de estribos)
Av = 2 x 1.29 cm² = 2.58 cm² (asumiendo 2 ramas Ø 1/2”)
Componente fuerza pretensado Vp=0
Cortante nominal resistente
El menor valor de Vn = 18,523kg + 50,293kg + 0 = 68,816kg
Vn = 0.25 x 280 x 30 x 69.62 + 0 = 146,202kg
Luego Vn = 68,816kg
Cortante resistente total
Vr = ØVn = 0.9(68,816 kg) = 61,934kg > 58,763Kg OK!
Refuerzo transversal mínimo
bv s
A v ≥ 0.083 fc' [SI] (5.8.2.5-1)
fy
' bv s
= A v ≥ 0.27 fc [MKS]
fy
30( )
15
A v ≥ 0.27 280 cm2
4200
A v mín = 0.48 cm² < 2.58 cm² OK !
Espaciamiento máximo del refuerzo transversal (Art. 5.8.2.7)
Vu − φVp
vu = (5.8.2.9-1)
φb v d v
Vu 58,763
vu = = = 31.26 kg / cm²
φb v d v 0.9(30)(69.62)
También:
si vu < 0.125f’c smáx= 0.8dv ≤ 60 cm (5.8.2.7-1)
si vu ≥ 0.125f’c smáx= 0.4dv ≤ 30 cm (5.8.2.7-2)](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-143-320.jpg)



![III-85
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
gint= 0.611 (ver diseño de viga interior)
Luego: 0.931(0.611
931(0.611) 0.569
g = 0.931(0.611) = 0.569
c) Art. 4.6.2.2.2d: Caso puentes de viga y losa con diafragmas rígidamente
conectados (ver también Apéndice III-C)
NL X Σe
R = + ext 2 (C4.6.2.2.2d-1)
Nb Σx
c.1) Un carril cargado:
P/2 P/2
0.60 1.80 .15
(Minimo)
R1
e=2.10
.375 .15 X =3.15
.30 ext
0.825 2.10 2.10 2.10 0.825
x=1.05
x=3.15
Con:
R = reacción sobre la viga exterior en términos de carril (ancho=3.60m)
NL = número de carriles cargados = 1
Nb = número de vigas = 4
e = excentricidad del camión de diseño o carga de carril respecto del
centro de gravedad del conjunto de vigas = 2.10m
Xext= distancia horizontal desde el centro de gravedad del conjunto de
vigas hasta la viga exterior = 3.15m
x = distancia horizontal desde el centro de gravedad del conjunto de
vigas hasta cada viga
1 3.15 m (2.1m)
R = + = 0.550
4 2[(3.15m)2 + ( .05 m)2 ]
1
Con el factor de presencia múltiple, m=1.2:
g = R = 1.2(0.550) = 0.660
0.660
c.2) Dos carriles cargados:
P/2 P/2
P/2 P/2
0.60 1.80 1.20 0.60 1.80
(Minimo)
R1 R2
e=2.10 e=1.50
1 2
.375 .15 X =3.15
.30 ext
0.825 2.10 2.10 2.10 0.825
x=1.05
x=3.15](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-147-320.jpg)
![III-86
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
2 3.15 m (2.10 m −1.50 m)
R = + = 0.586
4 2[(3.15 m)2 + ( .05 m)2 ]
1
Con el factor de presencia múltiple m=1.0:
g = R = 1.0(0.586) = 0.586
El factor de distribución crítico es, g= 0.660
0.660
d) De los casos a), b), y c), seleccionamos para el estado limite de resistencia el
factor de distribución de momento, g= 0.660
0.660
MLL+IM= 0.660(98.83 T-m) = 65.23T-m
B) Momento de Diseño, Estado Límite de Resistencia I
Con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(35.73) + 1.50(3.04) + 1.75(65.23) = 163.38T-m
Se sugiere al interesado y a manera de práctica, realizar el cálculo del acero
correspondiente.
C) Diseño por Corte
La sección crítica por corte por simplicidad la tomaremos al igual que en el
caso de la viga interior, a una distancia 0.82m del eje del apoyo.
Carga muerta (DC) C
L
270 kg 270 kg 270 kg
Con wDC=1,938kg/m
0.82
VDC = ( ,033 − 270)kg − 0.82m(
12 1938 kg / m) A B
= 10,174kg w = 1938 kg/m
DC
12 m
12,033 kg
Superficie de rodadura (DW)
0.82 w =169 kg/m
DW
Con wDW= 169kg/m A B
VDW = 1014 kg − 0.82m(
169kg / m)
= 875kg 12 m
1014 kg](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-148-320.jpg)

![III-89
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
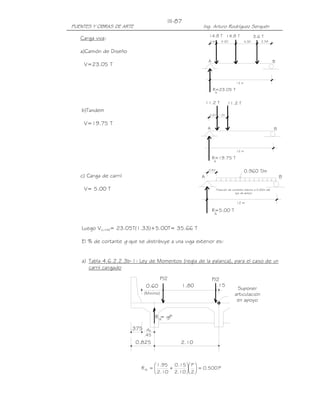
e = excentricidad del camión de diseño o carga de carril respecto del
centro de gravedad del conjunto de vigas = 2.10m
Xext= distancia horizontal desde el centro de gravedad del conjunto de
vigas hasta la viga exterior = 3.15m
x = distancia horizontal desde el centro de gravedad del conjunto de
vigas hasta cada viga
1 3.15 m (2.1m)
R = + = 0.550
4 2[(3.15m)2 + ( .05 m)2 ]
1
Con el factor de presencia múltiple, m=1.2:
g = R = 1.2(0.550) = 0.660
0.660
c.2) Dos carriles cargados:
P/2 P/2
P/2 P/2
0.60 1.80 1.20 0.60 1.80
(Minimo)
R1 R2
e=2.10 e=1.50
1 2
.375 .15 X =3.15
.30 ext
0.825 2.10 2.10 2.10 0.825
x=1.05
x=3.15
2 3.15 m (2.10 m −1.50 m)
R = + = 0.586
4 2[(3.15 m)2 + ( .05 m)2 ]
1
Con el factor de presencia múltiple m=1.0:
g = R = 1.0(0.586) = 0.586
El factor de distribución crítico es, g= 0.660
0.660
d) De los casos a), b), y c), seleccionamos para el estado limite de resistencia el
factor de distribución de cortante, g= 0.660
0.660
VLL+IM= 0.660(35.66T) = 23.54T](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-151-320.jpg)
![III-90
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
D) Cortante de Diseño, Estado Límite de Resistencia I
Con n= nDnRnI=1:
Vu = n[1.25 VDC + 1.50 VDW + 1.75 V(LL+IM)] (Tabla 3.4.1-1)
= 1.25(10.17) + 1.50(0.88) + 1.75(23.54) = 55.23T
Se sugiere al interesado y a manera de práctica, realizar el cálculo del acero por
corte correspondiente.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-152-320.jpg)
![III-91
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
IV)
IV) DISEÑO DE BARRERAS DE CONCRETO
Se propone en este caso un modelo de barrera de concreto con perfil basado en la
barrera de New Jersey. Cabe destacar que un sistema de barreras y su conexión a la
cubierta sólo se autoriza después de demostrar que es satisfactorio a través de
pruebas de choque en barreras a escala natural para el nivel de prueba deseado
[A13.7.3.1]. Si se realizan modificaciones menores a modelos ya probados, que no
afectan su resistencia, pueden utilizarse sin las pruebas de impacto requeridas.
0.375
.15 .175
.05
Ø12"@0.17
.47
7Ø3 8"
0.85
.25
Asfalto 2" .08
.05
Losa .20
A) Resistencia en flexión alrededor de un eje vertical a la barrera (Mw)
La resistencia a los momentos positivo y negativo que actúan alrededor de un eje
vertical se determina tomando como base el mecanismo de falla en este tipo de
barreras; se determina así el refuerzo horizontal en la cara vertical de la barrera (en
este caso 4Ø3/8”).
Para determinar el momento resistente se dividirá la sección de barrera en tres
partes: A1, A2 y A3, tal como se observa en el gráfico.
15 17.5
15 17.5 05
05 d1
7.50
17.9
19.75 z d2
A1 47 47
19.75
d3
A2 25cm 25
4Ø3 8" d4
A3 13 13](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-153-320.jpg)







![III-99
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
V) DISEÑO DE LOSA EN VOLADIZO
A) Criterios LRFD aplicables (Tabla 3.4.1-1)
Resistencia I: U = n[1.25DC+1.50DW+1.75(LL+IM)]
Evento Extremo II: U = n[1.0DC+1.0DW+1.0(LL+IM)]
B) Momentos de flexión por cargas (franja de 1.0m de ancho)
37.5
15 17.5
05
7.4T
0.30 x
(mínimo)
_
47 x=.13
A = 2028.75cm2 85 Asfalto 2"
barrera
_ 0.20 P = 487kg/m
barrera
x=13 25cm
0.375 0.30 .15 .15
Asfalto 2" 13
P = 487kg/m
barrera cara de viga
Considerando el momento flector en la cara de viga se tiene:
Carga muerta (DC):
wlosa = 0.20m x 1.0m x 2,400kg/m3 = 480kg/m
w losaL2 480(0.675)2
MDC, =
1 = = 109kg-m
2 2
El peso de la barrera es:
Pb = 0.202875m² x 1.0m x 2400kg/m³ = 487kg
MDC,2 = Pb (L − x) = 487kg (0.675m − 0.13m) = 265 kg − m
Luego: MDC = 109kg − m + 265kg − m = 374kg − m
Carga por superficie de rodadura (DW):
wasf 2” = 0.05m x 1.00m x 2250kg/m³ = 113 kg/m](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-161-320.jpg)
![III-100
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
113(0.30)2
MDW = = 5 kg − m
2
Carga viva (LL):
El ancho de franja en que se distribuye el eje de rueda es:
E= 1140+0.833X (Tabla 4.6.2.1.3-1)
Donde:
X = distancia entre la carga y el punto de apoyo (mm)
= 0.15m =150mm
Luego:
E= 1140+0.833(150) = 1265mm = 1.27m
El momento del eje de rueda vehicular distribuido en un ancho E=1.27m,
afectado por el factor de presencia múltiple (m=1.2), y el incremento por carga
dinámica (I=0.33) es:
7.4T( .2)( .33)
1 1
MLL +IM = .(0) = 0 kg − m
1.27m
Colisión vehicular (CT):
R =26.13T
w
H=0.85 L +2H= 2.22m+2x0.85m
C
= 3.92m
M
CT
Rw 26.13 T
MCT =
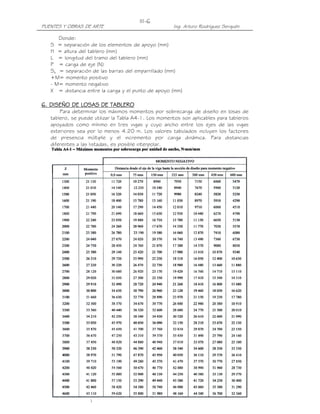
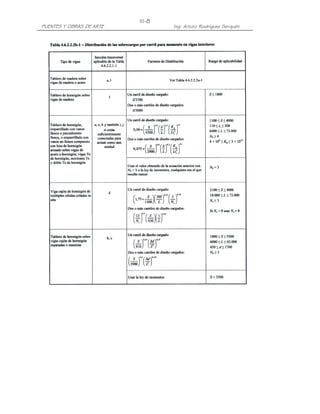
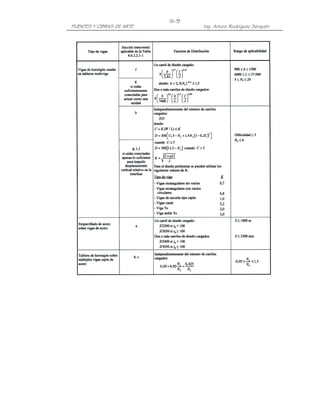
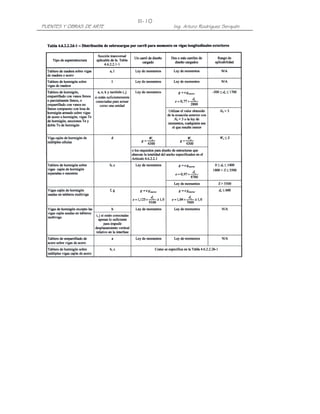
L + 2H (H) = 3.92m ( 0.85m) = 5.67 T − m
c
C) Cálculo del Acero
Para el Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(374) + 1.50(5) + 1.75(0) = 475kg-m = 0.48T-m](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-162-320.jpg)
![III-101
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Para el Estado Límite de Evento Extremo II, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.50 MDW + 1.00 MCT ] (Tabla 3.4.1-1)
= 1.25(374) + 1.50(5) + 1.00(5670) = 6145kg-m = 6.15T-m
2Ø1/2"@0.20
z
0.20 d
1Ø1/2"@0.19
Siendo este último momento el que rige, probaremos a usar 2∅ ½”@ 0.20m:
Mu= 6.15T-m
As(-)= 2.58cm² / 0.20m = 12.9 cm²/m
r = recubrimiento = 5.0cm (Tabla 5.12.3-1)
1.27
z = 5.0 + = 5.64 cm
2
d= 20cm – 5.64cm = 14.36cm
Ø = 1.0 (Caso de Eventos Extremos, AASHTO 1.3.2.1)
A s fy 12.90x4200
a= '
= = 2.28 cm
0.85fc b 0.85x280x
100
a 2.28
ØMn = ØA s fy (d − ) = 1.0( .90)(4200)( .36 −
12 14 ) = 7.16 T − m
2 2
Este momento debe reducirse por la fuerza de tensión axial ejercida por la
colisión en el volado, T = R w :
L c + 2H
T M
0.20 CT T](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-163-320.jpg)


![III-104
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
x B w =0.48 T /m C D G
E A losa
RD=0.89T
RA=0.89T R =1.02T RC=1.02T
B
0.825 2.10 2.10 2.10 0.825
CARGA DE LOSA Y REACCIONES EN APOYOS
P =0.487T P =0.487T
barrera barrera
0.13 x 0.13
A B C D
E G
RD=0.68T
RA=0.68T R =0.19T RC=0.19T
0.825 2.10 B 2.10 2.10 0.825
CARGA DE BARANDAS Y REACCIONES EN APOYOS
En el primer tramo interior de la losa se tienen las siguientes expresiones de
momento flector:
Carga Muerta (DC):
(0.825 + x)2
Losa : Mx = −0.48 + 0.89 x
2
Barrera: Mx = -0.487(0.695+x) + 0.68x
Carga por superficie de rodadura (DW):
Se despreciará por ser muy pequeña.
CT):
Carga por colisión vehicular (CT):
5.67
MCT = − ( .40 − x)
1
1.40
La distancia x se encuentra igualando Mu = 3.73T-m, con el momento
correspondiente al Evento Extremo II:
−3.73 = 1.0 [ .25MDC, x +1.0MCT, x ]
1
(0.825 + x)2 5.67
− 3.73 = 1.25− 0.48 + 0.89 x − 0.487(0.695 + x) + 0.68 x +1.0− ( .40 −
1 x)
2 1.40
Resolviendo, x = 0.54m.
Se agregará además (5.11.1.2) la longitud de 15db=15(1.27cm)=0.19m](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-166-320.jpg)


![III-107
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Carga distribuida por peso propio del diafragma:
wpp = 0.25m x 0.70m x 2400kg/m3 = 420 kg/m
Resolviendo la viga hiperestática tenemos:
Carga por superficie de rodadura (DW):
Se despreciará por ser muy pequeña.
Carga viva y efecto de carga dinámica (LL+IM):
Con el momento por carga viva encontrado en el cálculo de la losa (Método
A) y la consideración de los factores de presencia múltiple y carga dinámica
en estado límite de resistencia, considerando que la viga diafragma toma
toda la carga viva tenemos para la cara derecha de la viga en B:
MLL +IM = −2.04T − m x1.2 x1.33 = −3.26T − m
Combinación crítica:
Para el Estado Límite de Resistencia I, con n= nDnRnI=1, cara derecha de la viga
en B:
Mu = n[1.25 MDC + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(-0.106) + 1.75(-3.260) = -5.84 T-m
Cálculo del acero negativo:
Utilizando acero principal 2∅5/8” (As=4.0cm2) colocado debajo del acero de la
losa (Ø1/2”), estribos ∅ 3/8” y recubrimiento r= 5.0 cm (Tabla 5.12.3-1):](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-169-320.jpg)

![III-109
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Carga por superficie de rodadura (DW):
Se despreciará por ser muy pequeña.
Carga viva y efecto de carga dinámica (LL+IM):
Con el momento por carga viva encontrado en el cálculo de la losa (Método A) y la
consideración de los factores de presencia múltiple y carga dinámica en estado
límite de resistencia, considerando que la viga diafragma toma toda la carga viva
tenemos en F:
MLL +IM = 2.723T − m x1.2 x1.33 = 4.35T − m
Combinación crítica:
Para el Estado Límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.25 MDC + 1.75 M(LL+IM)] (Tabla 3.4.1-1)
= 1.25(0.083) + 1.75(4.350) = 7.72 T-m
Cálculo del acero positivo:
Habiendo utilizado para el acero negativo 2Ø5/8” con capacidad Mu =9.16 T-m,
utilizaremos la misma cantidad de acero principal para el acero positivo donde el
momento actuante: Mu =7.72 T-m es menor.
USAR 2∅5/8”
C) Armadura de contracción y temperatura en caras laterales (Art. 5.10.8)
En el alma de la viga diafragma:
As=2Ø5/8"
Ag .20
A s mín = 0.756 [SI] (5.10.8.2-1)
Fy
A s mín = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ] .70 2Ø1/2"
A s mín = 0.0018x[25(70 − 20)] = 2.25cm2 As=2Ø5/8"
.25
A s mín = 1.13 cm2 / cara
Usaremos por cara: 1 Ø 1/2” (1.29 cm2) , con la consideración:
s máx = 3t = 3 (25) = 75 cm y s máx = 45 cm OK!](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-171-320.jpg)


![III-112
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Con la posición del camión de diseño mostrada:
VLL=7.4T(-0.739)+7.4T(-0.075) = -6.02 T
Con el factor de carga dinámica IM=0.33 y el factor de presencia múltiple
m=1.2, considerando que la viga diafragma toma toda la carga viva:
VLL+IM= -6.02T(1.33)(1.2) = -9.61 T
Combinación crítica, Estado Límite de Resistencia I, con n= nDnRnI=1:
Vu = n[(1.25 ó 0.9)VDC + 1.75 V(LL+IM)] (Tabla 3.4.1-1)
Vu = 0.9(+138kg)+ 1.75(-9,610kg) = -16,693 kg
Diseño de estribos:
Cortante actuante : Vu = 16,693 kg
Cortante resistente : Vr = Ø Vn (5.8.2.1-2)
Ø = 0.9 (5.5.4.2)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdv + Vp (5.8.3.3-2)
Donde:
'
Cortante resistente concreto Vc = 0.083β fc b v d v [N] (5.8.3.3-3)
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc' b v d v [kg]
A v fy d v (cot θ + cot α )senα
Cortante resistente acero: Vs = (5.8.3.3-4)
s
con ᒕ = 45° (Art. 5.8.3.4) A v fy d v
α = 90° (ángulo de inclinación del estribo) Vs =
s
Cortante resistente concreto (Vc)
' '
Vc = 0.083β fc b v d v [N] = 0.53 fc b v d v [kg] = 0.53 280 (25 x60.59)
Vc = 13,434 kg
siendo bv = ancho del alma= 25 cm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-174-320.jpg)
![III-113
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Cortante resistente del acero (Vs)
Se propone estribos Ø3/8” espaciados cada 45 cm. Luego:
A v fy d v (cot θ + cot α)senα A v fy d v 1.42( 4200)(60.59)
Vs = = = = 8, 030 kg
s s 45
donde:
s = 45 cm (espaciamiento asumido de estribos)
Av = 2 x 0.71 cm² = 1.42 cm² (asumiendo 2 ramas Ø 3/8”)
Componente fuerza pretensado Vp=0
Cortante nominal resistente
El menor valor de Vn = 13,434 kg + 8,030 kg + 0 = 21,464 kg
Vn = 0.25 x 280 x 25 x 60.59 + 0 = 106,033 kg
Luego Vn = 21,464 kg
Cortante resistente total
Vr = ØVn = 0.9(21,464 kg) = 19,318 kg > 16,693 Kg OK!
Refuerzo transversal mínimo
bv s
A v ≥ 0.083 fc' [mm2 ] (5.8.2.5-1)
fy
bv s
A v ≥ 0.27 fc' [cm2 ]
fy
25(45)
A v ≥ 0.27 280 cm2
4200
A v mín = 1.21 cm² < 1.42 cm² OK !
Espaciamiento máximo del refuerzo transversal (Art. 5.8.2.7)
Vu − φVp
vu = (5.8.2.9-1)
φb v d v
Vu 16, 693
vu = = = 12.24 kg / cm²
φb v d v 0.9(25)(60.59)
También:
si vu < 0.125f’c smáx= 0.8dv ≤ 60 cm (5.8.2.7-1)
si vu ≥ 0.125f’c smáx= 0.4dv ≤ 30 cm (5.8.2.7-2)](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-175-320.jpg)



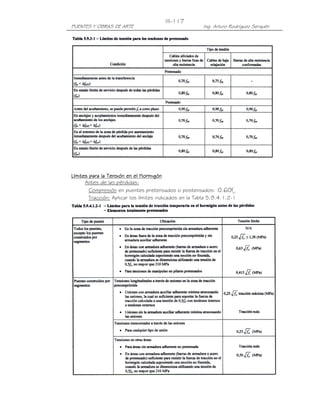








![III-126
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
[
k g = n I + Ae 2
g ] =1[8' 779, 520 + 4560(85) ] = 41' 725, 520 cm
2 4
0.1 0.1
kg 41725, 520
'
3
Lt = = 1.09
s 18 3
3000( )
2000 0.6 2000 0.2
g = 0.075 + ( ) ( ) ( .09) = 0.58
1
2900 30000
- Un carril cargado:
S 0.4 S 0.3 k g 0.1
g = 0.06 + ( ) ( ) ( 3) (Tabla 4.6.2.2.2b-1)
4300 L Lt s
2000 0.4 2000 0.3
g = 0.06 + ( ) ( ) ( .09) = 0.42
1
4300 30000
Luego: MLL+IM = 0.58 (387.09 T-m)= 224.51 T-m
Entonces: Md+ l = 25.31 + 224.51 = 249.82 T − m
Resumen:
Cargas iniciales: Mo = 243.61 T- m
Cargas de servicio: Md+ l = 249.82 T − m
Mt = 493.43 T- m
Esfuerzos Permisibles
Iniciales (transferencia)
Fibra superior:
'
fti = 0.25 fci ≤ 1.38 MPa [SI] (Tabla 5.9.4.1.2-1)
= 0.80 fci ≤ 14 kg / cm2
'
[MKS]
= 0.80 280 = 13.39 kg / cm2 ≤ 14 kg / cm2
Fibra inferior:
'
fci = −0.60 fci (Art. 5.9.4.1.1)
2
= −0.60 (280) = −168 kg / cm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-188-320.jpg)


![III-129
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Se tomará: emáx real = 114.86cm -15cm = 99.86cm
99.86cm
De la inecuación (3), en el centro de luz:
1
Con e = 99.86 cm, = 2.139x −6 kg −1,
10
Pi
467.36
Pi = 467.36 T
E) ESTADOS LÍMITES APLICABLES (Tabla 3.4.1-1)
Servicio I: U=n[1.00(DC+DW) + 1.00(LL+IM)]
Servicio III: U=n[1.00(DC+DW) + 0.80(LL+IM)]
Resistencia I: U=n[1.25(DC) + 1.50(DW) + 1.75(LL+IM)]
Se hará uso de n= nDnRnI=1
F) COMPROBACIÓN DE ESFUERZOS EN CENTRO DE LUZ
F.1) ESTADO DE SERVICIO I
En condiciones iniciales:
Fibra superior (ecuación 1)
Pi Pi e Mo 467,360 467,360(99.86) 243.61105
x
fti = − + − =− + −
A S1 S1 8505 431 421
, 431 421
,
fti = -3.24 kg/cm2 (comp) < admitido: fti = +13.39 kg/cm2 (tracción) OK!
Fibra inferior (ecuación 2)
Pi Pi e Mo 467,360 467,360(99.86) 243.61105
x
fci = − − + =− − +
A S2 S2 8505 207,109 207,109
fci = -162.67 kg/cm2 (comp) < admitido: fci = -168 kg/cm2 (comp) OK!
En condiciones finales:
Con P = R Pi = 0.85(467.360 T) = 397.256 T
Fibra superior (ecuación 4)
CASO I (carga total)
R Pi R Pi e Mt
fcs = − + −
A S1 S1](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-191-320.jpg)
![III-130
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
397, 256 397, 256(99.86) 243.61105 25.3110 5 224.5110 5
x x x
fcs = − + − + +
8505 431 421
, 431 421
, 431 421
, 431 421
,
fcs = −46.71+ 91.95 − 56.47 − 5.87 − 52.04
fcs = -69.13 kg/cm2 (comp) < admitido: fcs = -210 kg/cm2 (comp) OK!
CASO II (sobrecarga y semisuma de presforzado+cargas permanentes)
Ml 1 R Pi R Pi e Mpp + asf
fcs = − + − + −
S1 2 A S1 S1
224.5110 5 1 397, 256 397, 256(99.86) 243.6110 5 25.31105
x x x
fcs = − + − + − −
431 421
, 2 8505 431 421
, 431 421
, 431 421
,
1
fcs = −52.04 + [− 46.71+ 91.95 − 56.47 − 5.87]
2
fcs = -60.59 kg/cm2 (comp) < admitido: fcs = -140 kg/cm2 (comp) OK!
Fibra inferior (ecuación 3)
R Pi R Pi e Mt 397, 256 397, 256(99.86) 493.43x 5
10
fts = − − + =− − +
A S2 S2 8505 207,109 207,109
fts =0 kg/cm2 admitido: fts = 0 kg/cm2 (no tracciones) OK!
F.2) ESTADO DE SERVICIO III
En condiciones iniciales:
Fibra superior (ecuación 1)
Pi Pi e Mo 467,360 467,360(99.86) 243.61105
x
fti = − + − =− + −
A S1 S1 8505 431 421
, 431 421
,
fti = -3.24 kg/cm2 (comp) < admitido: fti = +13.39 kg/cm2 (tracción) OK!
Fibra inferior (ecuación 2)
Pi Pi e Mo 467,360 467,360(99.86) 243.61105
x
fci = − − + =− − +
A S2 S2 8505 207,109 207,109
fci = -162.67 kg/cm2 (comp) < admitido: fci = -168 kg/cm2 (comp) OK!](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-192-320.jpg)










![III-141
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
III-
APÉNDICE III-C
MÉTODO DE COURBON PARA DISTRIBUIR LA CARGA VIVA EN VIGAS DE UN
DISTRIBUIR
PUENTE VIGA-LOSA
VIGA-
Cuando una sección transversal de puente se deforma y gira como una sección
transversal rígida, esto es el caso de secciones de losa y vigas de concreto con vigas
diafragmas convenientemente distribuidas e interconectadas, es posible repartir la
carga transversalmente entre las vigas de soporte según la expresión de Courbon:
P Pe
R = ± X
n Ι
Es decir:
1 eX
R = P ±
n
X2
∑
donde X es la distancia de una viga al centroide de las vigas principales, ∑X 2
es la
suma de los cuadrados de las distancias de varias vigas principales desde el
mencionado centroide, n el número de vigas principales. El reglamento AASHTO LRFD
adopta esta fórmula según C4.6.2.2.2d-1, para calcular el porcentaje de distribución
de la carga viva “g” en vigas.
Veamos el siguiente caso, donde se quiere distribuir la carga de un carril de diseño
entre las cuatro vigas que se muestran en la figura.
P/2 P/2
0.60 1.80 .15
(Minimo)
e=2.10
1
R=P
R1 R2 R3 R4
X =3.15
ext
2.10m 2.10 2.10
X=1.05
X=3.15m
Se tiene: Ι= ∑X 2
[
= 2 3.152 + 1.052 = 22.05 ]
y también: n=4, e=2.10m](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-203-320.jpg)




















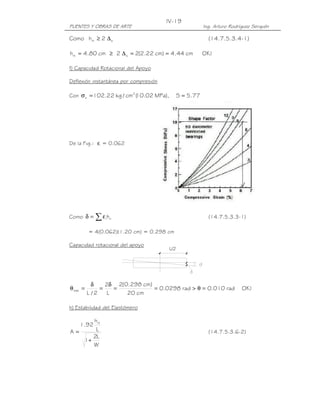





![V-4
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Coeficiente de Empuje Lateral en Reposo, ko
Para suelos normalmente consolidados, muro vertical y terreno nivelado, el
coeficiente de empuje lateral en reposo se puede tomar como:
ko = 1 - senφ'f
Para suelos sobreconsolidados:
ko = (1 - senφ'f) (OCR )senφ'f
donde:
φ'f = ángulo efectivo de fricción del suelo
ko = coeficiente de empuje lateral del suelo en reposo
OCR = relación de sobreconsolidación
Coeficiente de Empuje Lateral Activo, ka
sen 2 ( θ + φ' f ) (3.11.5.3-1)
ka =
[
Γ sen 2 θ.sen( θ − δ) ]
donde:
2
sen ( φ' f + δ ).sen ( φ' f −β )
Γ = +
1 (3.11.5.3-2)
sen ( θ − δ ).sen ( θ + β )
δ = ángulo de fricción entre relleno y muro (ver Tabla 3.11.5.3-1)
β = ángulo que forma la superficie del relleno respecto de la horizontal
θ = ángulo que forma el respaldo del muro respecto de la horizontal
φ'f = ángulo efectivo de fricción interna
Notar que para δ = β = 0, θ =90°, el valor ka de las expresiones anteriores
(teoría de de Coulumb) es:
Ø
k a = tg 2 ( 45 − ) (teoría de Rankine)
2](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-230-320.jpg)

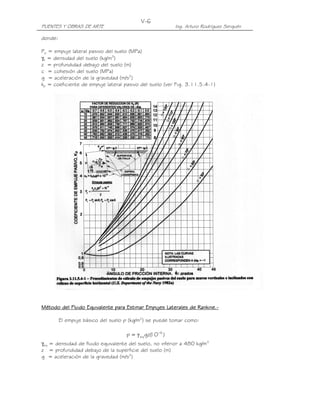





![V-12
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
• La cuña activa de suelo que define la superficie de falla y carga el muro, es
plana.
• Las aceleraciones son uniformes a través de la masa de suelo retenido.
La presión del terreno incluyendo la acción sísmica, se determina con:
1
E AE = k AE γ t (( − k v )H2
1 (A.11.1.1.1-1)
2
siendo el coeficiente de presión activa sísmica del terreno:
cos 2 ( φ − θ − β)
k AE = 2
(A.11.1.1.1-2)
.
2 sen(φ + δ)sen(φ − θ − I )
cos θ cos β cos(δ + β + θ) +
1 .
cos(δ + β + θ) cos( I − β)
donde:
γt = peso unitario del terreno
H = altura del terreno retenida por el muro
kv = coeficiente de aceleración vertical
kh = coeficiente de aceleración horizontal
φ = ángulo de fricción interna del suelo
Ө= arc tan [kh /(1- kv)]
β = ángulo de inclinación del muro con la vertical (sentido negativo como se ilustra)
δ = ángulo de fricción entre el suelo y el estribo
i = ángulo de inclinación del material de relleno con la horizontal](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-238-320.jpg)

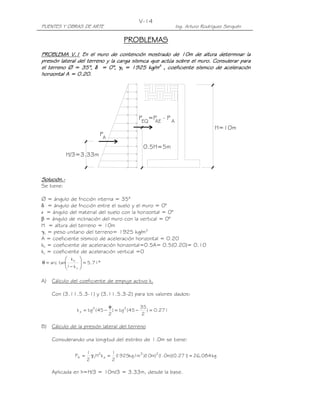


![V-17
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
BR = 300 kg/m
altura equivalente de suelo por S/C
P = 7,000 kg/m
DC
1.80 P = 800 kg/m
DW
P = 9,000 kg/m LS1 h' = 0.80 S/C por carga viva (LS)
LL+IM
.30
.80 .15
.40
DC
5
WS = 150 kg/m .25.25 0.50
LS2 = 3.70m x 365 kg/m² =1350 kg/m
CR+SH+TU = 900 kg/m
EH2 = 3.70m x 198 kg/m²= 734 kg/m
s=18.43°
H = 4.00 m DC
3
DC EH1= 0.5 x 3.7m x 1687 kg/m²
2 = 3121 kg/m
EV
1
.30 .17
DC1 õ = 24°
.30
0.50
0.90
EV
0.50 EV 3
2 DC
4
A ka x 3.70m x 1600 kg/m³ = 1687 kg/m²
B = 2.50 m ka x 0.30m x 2320 kg/m³ = 198 kg/m²
ka x 0.80m x 1600 kg/m³ = 365 kg/m²
ESTRIBO
CASO I – ESTRIBO CON PUENTE
A) Coeficiente de empuje activo Ka
∅ = ángulo de fricción interna = 31°
δ = ángulo de fricción entre el suelo y el muro = 24° (Tabla 3.11.5.3-1)
β = ángulo del material del suelo con la horizontal = 0°
ᒕ = ángulo de inclinación del muro del lado del terreno = 90°
Luego:
2
sen ( φ + δ) sen (φ − β)
Γ=+
1 (3.11.5.3-2)
sen ( θ − δ) sen ( θ + β)
Para β = 0° y ᒕ = 90° :
2
sen (φ + δ) senφ
Γ=+
1 = 2.821
cos δ
sen2 ( θ + φ)
ka = (3.11.5.3-1)
[
Γ sen2 θ sen (θ − δ) ]
cos2 φ
Para ᒕ = 90° : ka = = 0.285
Γ cos δ](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-243-320.jpg)













![V-41
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
CARGAS EN BASE DE PANTALLA
CARGA CARGA DISTRIBUIDA (Ton/m) Carga(Ton) YP(m) M(T-
M(T-m)
LS p”=0.333x0.60x1.925=0.385 0.385x5.90=2.27 2.95 6.70
EH p=0.333x5.90x1.925=3.786 0.5x5.90x3.786=11.17 1.97 21.96
EQterr p’=0.5(0.4330.333)5.9x1.925=0.566 0.566x5.90=3.34 2.95 9.84
PEQ - 4.97 5.15 25.59
EQestri - 6.20 2.80 17.33
BR - 1.99 7.70 15.32
Donde para EQestr :
W = peso estribo y terreno tributario sobre P =7.61 + 33.72= 41.33Ton/m
Kh=0.5A
EQestrib=Kh.W=0.15x41.33Ton/m = 6.20Ton/m
YP = C.G. del estribo y terreno tributario sobre P = 2.80m
a) Acero Por Flexión
Momento de diseño en la base de la pantalla:
Estado límite de Resistencia I, con n= nDnRnI=1:
Mu = n[1.75MLS + 1.50MEH + 1.75MBR] (Tabla 3.4.1-1)
= 1.00[1.75(6.70T-m)+1.50(21.96T-m)+1.75(15.32T-m)]
= 71.49T-m
Estado límite de Evento Extremo I, con n= nDnRnI=1:
Mu = n[0.50MLS + 1.50MEH + 1.00MEQ + 0.50MBR] (Tabla 3.4.1-1)
=1.00[0.50(6.70T-m)+1.50(21.96T-m)+1.00(9.84+25.59+17.33)T-m
+0.50(15.32T-m)] = 96.72T-m
Con Mu= 96.72T-m, As= 1∅1”, recubrimiento r= 7.5cm (Tabla 5.12.3-1)
2.54
z = 7.5 + = 8.77 cm
2
d= 90cm – 8.77cm =81.23cm
A s fy A s x4200 z d
a= '
= = 6.97cm
0.85fc b 0.85x210x 100
90cm
Mu 96.00x 5
10 5.10
As = = = 29.62cm², s Ø1" = = 0.17m
a a 29.62
Ø f fy (d − ) 1.0x4200(81.23 − )
2 2
(Øf=1.0, según Art. 11.6.5 para estado límite de Evento Extremo)](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-267-320.jpg)
![V-42
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
As máximo (Art. 5.7.3.3.1)
Una sección no sobre reforzada cumple con: c /de ≤ 0.42
c = a / β1 = 6.97cm / 0.85 = 8.20cm
de = 81.23cm
c /de = 0.10 ≤ 0.42 OK!
As mínimo (Art. 5.7.3.3.2)
La cantidad de acero proporcionado debe ser capaz de resistir el menor valor
de1.2Mcr y 1.33Mu:
a) 1.2Mcr = 1.2fr S = 1.2(29.13kg/cm2)(135,000cm3) = 47.19T-m
Siendo:
fr = 0.63 fc MPa = 2.01 fc kg / cm2 = 2.01 210 = 29.13 kg / cm2
' '
S = bh2/6 = 100(90)2/6 = 135,000cm3
b) 1.33 Mu= 1.33(96.72T-m) = 128.64T-m
El menor valor es 47.19T-m y la cantidad de acero calculada (29.62cm2)
resiste Mu=96.72T-m >47.19T-m OK!
0.1
USAR 1∅1” @ 0.17m
b) As de temperatura
Ag
A s temp = 0.756 [SI] (5.10.8.2-1)
Fy
A s temp = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ]
Siendo la pantalla de sección variable, tomamos conservadoramente un grosor
de 0.80m:
100) = 16.2 cm2
A s temp = 0.0018(90x
A s temp = 16.2 cm2 / 2 = 8.10 cm2 / capa
2.00
Utilizando varillas ∅5/8”, la separación será: s = = 0.24 m
8.10
smáx = 3t = 3(0.90)= 2.70m (Art.5.10.8)
smáx = 0.45m OK! (Art.5.10.8)
0.24
USAR 1∅5/8” @ 0.24 m
Nota.- El acero de temperatura se colocará por no contar con ningún tipo de
acero en el sentido perpendicular al acero principal de la pantalla y también en
la cara de la pantalla opuesta al relleno, en ambos sentidos.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-268-320.jpg)


![V-45
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
corte
d) Revisión por corte
Típicamente el corte no gobierna el diseño de un muro de contención; sin
embargo revisaremos el grosor de la pantalla para confirmar que no se
requiere armadura transversal.
El cortante actuante en la base de la pantalla para el estado límite de
Resistencia I, con n= nDnRnI=1, es:
Vu = n[1.75 VLS+1.50 VEH +1.75 VBR] (Tabla 3.4.1-1)
= 1.00[1.75(2.27T) + 1.50(11.17T)+1.75(1.99T)]
= 24.21T
El cortante actuante en la base de la pantalla para el estado límite de Evento
Extremo I, con n= nDnRnI=1, es:
Vu = n[0.5 VLS+1.50 VEH +1.00 VEQ +0.5 VBR] (Tabla 3.4.1-1)
=1.00[0.5(2.27T)+1.50(11.17T)+1.0(3.34+4.97+6.20)+0.5(1.99T)]
= 33.39T
Luego Vu = 33.39T
El cortante resistente del concreto es:
V r = Ø Vn (5.8.2.1-2)
Ø = 1.0 (Art. 11.6.5)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdv + Vp (5.8.3.3-2)
'
Vc = 0.083β fc b v d v [N] (5.8.3.3-3)
'
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc b v d v [kg]
'
Vc = 0.53 fc b v d v = 0.53 210 (
100 x77.75) = 59.71T
donde:
bv = ancho de diseño de pantalla= 100 cm
de = 81.23cm
a 6.97
d v = peralte de corte efectivo = d e − = 81.23 − = 77.75 cm (Art.
2 2
5.8.2.9)
no menor que el 0.90de= 0.90(81.23 cm) = 73.11cm OK!
mayor valor de 0.72h = 0.72(90 cm) = 64.80cm](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-271-320.jpg)
![V-46
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Con Vp=0 y Vs=0 Vn = 59.71T
el menor valor de Vn = 0.25 x 210 x 100 x 77.75 = 408.19T
es: Vn = 59.71T
La resistencia del concreto al corte es:
Vr = ØVn = 1.0(59.72T) = 59.71T > 33.39T OK!
9.71 3.39T
2) DISEÑO DE CIMENTACIÓN
a) Acero parte superior de zapata
Terreno equiv. por s/c
LS y=2.75mx0.60mx1.0mx1.925T/m3
h'=0.60
=3.18T
1.90
0.60
1.73
5.90 EV=33.73T
1.61
3.10
2.75 .35
3
DC =3.10mx1.0mx1.10mx2.4T/m =8.18T
As superior
1.10 Talón
q
B-2e
B
Momento de diseño en cara vertical de pantalla, estado límite de Resistencia
Ib, con n= nDnRnI=1, despreciando del lado conservador la reacción del suelo:
Mu = n[1.25 MDC +1.35 MEV +1.75 MLS] (Tabla 3.4.1-1)
= 1.00[1.25(8.18T x 1.55m) + 1.35(33.73T x 1.61m)
+ 1.75(3.18T x 1.73m)]
= 98.78T-m
Omitimos el estado de Evento Extremo I, pues no es crítico en este caso.](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-272-320.jpg)

![V-48
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Nota.- El acero de temperatura se colocará por no contar con ningún tipo de
acero, perpendicular al acero de flexión, tanto en el talón como en la punta del
cimiento.
c) Revisión del talón por corte
El cortante actuante en el talón para el estado límite de Resistencia I, con n=
nDnRnI=1, es:
Vu = n[1.25 VDC + 1.35 VEV +1.75 VLS] (Tabla 3.4.1-1)
= 1.00[1.25(8.18T) + 1.35(33.73T) +1.75(3.18T)]
= 61.32T
Se omite el estado de Evento Extremo I, pues no gobierna el diseño.
El cortante resistente del concreto es:
Vr = Ø Vn (5.8.2.1-2)
Ø = 0.9 (5.5.4.2)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdv +Vp (5.8.3.3-2)
'
Vc = 0.083β fc b v d v [N] (5.8.3.3-3)
'
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc b v d v [kg]
'
Vc = 0.53 fc b v d v = 0.53 210 (
100 x98.10) = 75.35T
donde:
bv = ancho de diseño de zapata = 100 cm
de = 101.23cm
a 6.27
d v = peralte de corte efectivo = d e − = 101.23 − = 98.10 cm (Art.
2 2
5.8.2.9)
no menor que el 0.90de= 0.90(101.23cm) = 91.11cm OK!
mayor valor de 0.72h = 0.72(110cm) = 79.20cm
Con Vp=0 y Vs=0 Vn = 75.35T
el menor valor de Vn = 0.25 x 210 x 100 x 98.10 =515.03T
es: Vn = 75.35T
La resistencia del concreto al corte es:
Vr = ØVn = 0.9(75.18T) = 67.81T > 61.32T OK!
67.81T
81 1.32T](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-274-320.jpg)

![V-50
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
As mínimo (Art. 5.7.3.3.2)
La cantidad de acero proporcionado debe ser capaz de resistir el menor valor
de1.2Mcr y 1.33Mu:
a) 1.2Mcr = 1.2fr S = 1.2(29.13kg/cm2)(201,667 cm3) = 70.49T-m
Siendo:
fr = 0.63 fc MPa = 2.01 fc kg / cm2 = 2.01 210 = 29.13 kg / cm2
' '
S = bh2/6 = 100(110)2/6 = 201,667cm3
b) 1.33 Mu= 1.33(26.98T-m) = 35.88T-m
El menor valor es 35.88T-m y la cantidad de acero propuesta (8.70cm2)
resiste Mu=36.79T-m >35.88T-m OK!
5/8” 0.23
23m
USAR 1∅5/8” @ 0.23m
e) Revisión de la punta por corte
corte
Cálculo de dv (Art. 5.8.2.9):
a 2.05
d v = peralte de corte efectivo = de − = 101.7 − = 100.68 cm
2 2
no menor que el 0.90de= 0.90(101.7cm) = 91.53cm OK!
mayor valor de 0.72h = 0.72(110cm) = 79.20cm
Debiendo tomar el cortante actuante a una distancia dv de la cara de la
pantalla, el cortante actuante es:
Vu = q u (L punta − d v ) = 44.3T / m2 ( .10m −1.01 ) = 4.11Ton / m
1 m
El cortante resistente del concreto es:
Vr = Ø Vn (5.8.2.1-2)
Ø = 1.0 (Art. 11.6.5)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdv + Vp (5.8.3.3-2)
'
Vc = 0.083β fc b v d v [N] (5.8.3.3-3)
'
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc b v d v [kg]
'
Vc = 0.53 fc b v d v = 0.53 210 ( 100.68) = 77.33T
100 x
Con Vp=0 y Vs=0 Vn = 77.33T
el menor valor de Vn = 0.25 x 210 x 100 x 100.68 =528.57T
es: Vn = 77.33T](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-276-320.jpg)



![VI-3
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
- Para elementos con armadura en espiral:
[
Pn = 0.85 0.85fc' (A g − A st ) + fy A st ] (5.7.4.4-2)
- Para elementos zunchados:
[
Pn = 0.80 0.85fc' (A g − A st ) + fy A st ] (5.7.4.4-3)
donde:
Pr = resistencia axial mayorada, con o sin flexión
Pn = resistencia axial nominal, con o sin flexión
f’c = resistencia especificada del hormigón a 28 días
Ag = área bruta de la sección
Ast = área total de la armadura longitudinal
fy = tensión de fluencia especificada de la armadura
Ø = factor de resistencia (Art. 5.5.4.2)
4. FLEXIÓN BIAXIAL (Art. 5.7.4.5)
En vez de realizar un análisis en base a condiciones de equilibrio y compatibilidad de
deformaciones para flexión biaxial, los elementos no circulares solicitados a flexión
biaxial y compresión se pueden dimensionar utilizando las siguientes expresiones
aproximadas:
- Si la carga axial mayorada es mayor o igual que 0.10 Ø f’cAg :
1 1 1 1
= + − (5.7.4.5-1)
Prsy Prx Pry Ø P0
siendo:
P0 = 0.85fc' ( A g − A st ) + A st fy (5.7.4.5-2)
- Si la carga axial mayorada es menor que 0.10 Ø f’cAg :
Mux Muy
+ ≤ 1.0 (5.7.4.5-3)
Mrx Mry
donde:
Ø = factor de resistencia para elementos solicitados a compresión axial
Prxy = resistencia axial mayorada en flexión biaxial
Prx = resistencia axial mayorada determinada sobre la base de que la excentricidad ey
es la única presente
Pry = resistencia axial mayorada determinada sobre la base de que la excentricidad ex
es la única presente
Pu = fuerza axial mayorada aplicada
Mux = momento mayorado aplicado respecto del eje X](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-280-320.jpg)









![VI-13
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
E s 2'039,400 kg / cm2
n= = =9
Ec 222,356 kg / cm2
Ast= n As = 413.10 cm²
(fs / n)
7.86 (+)
c=92.14 - y
92.14 100 cm E.N.
y
(-)
f 'c
100 cm
Área de acero transformada:
Ast = relación modular x área de acero
Ast = 9(45.90 cm2) = 413.10 cm2
Momentos respecto del eje neutro para determinar y:
100y (y/2) = 413.10 (92.14-y)
y = 23.77 cm
Inercia respecto del eje neutro de sección transformada:
by 3
I = A st (d s − y )2 +
3
100 (23.77) 3
= 413.10 (92.14 − y )2 +
3
= 2’378,697 cm4
c= 92.14 cm – 23.77 cm = 68.37 cm
Luego:
Ms c 95 x 105 x 68.37
fs = n= x 9 = 2,457 kg / cm2
I 2' 378, 697
fs = 2, 457 kg / cm2 < fsa = 2, 520 kg / cm2 OK !
A.5) Armadura de contracción y temperatura en caras laterales (Art. 5.10.8)
Ag
A s temp = 0.756 [SI] (5.10.8.2-1)
Fy
A s temp = 0.0018 A g [MKS, con fy = 4200 kg / cm2 ]](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-290-320.jpg)

![VI-15
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
A.7) Diseño por Corte
Cortante actuante : Vu = 200,000 kg
Cortante resistente : V r = Ø Vn (5.8.2.1-2)
Ø = 0.9 (5.5.4.2)
Vn = Vc+Vs+ Vp (5.8.3.3.-1)
siendo Vn el menor de:
Vn = 0.25f’cbvdb + Vp (5.8.3.3-2)
Donde:
'
Cortante resistente concreto Vc = 0.083β fc b v d v [N] (5.8.3.3-3)
para β=2 (Art. 5.8.3.4): Vc = 0.53 fc' b v d v [kg]
A v fy d v (cot θ + cot α)senα
Cortante resistente acero: Vs = (5.8.3.3-4)
s
con ᒕ = 45° (Art. 5.8.3.4) A v fy d v
α = 90° (ángulo de inclinación del estribo) Vs =
s
Cortante resistente concreto (Vc)
Vc = 0.083β fc b v d v [N] = 0.53 fc' b v d v [kg] = 0.53 210 (
'
100 x86.74)
Vc = 66,620 kg
siendo:
bv = ancho de la viga= 100 cm
a 10.80
d v = de − = 92.14 − = 86.74 cm
2 2
no menor que el mayor valor de 0.9de = 0.9(92.14 cm) = 82.93 cm OK!
0.72h = 0.72(100 cm) = 72 cm
Cortante resistente del acero
A v fy d v (cot θ + cot α)senα A v fy d v 8(4200)(86.74)
Vs = = = = 166, 541kg
s s 17.5
Estribos: 4 ramas Ø 5/8"](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-292-320.jpg)
![VI-16
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
donde:
Av = 4 x 2.00 cm² = 8 cm² (asumiendo 4 ramas Ø 5/8”)
s = 17.5 cm (espaciamiento asumido de estribos)
ᒕ = 45° (sección no presforzada) (5.8.3.4)
α = 90° (ángulo de inclinación del estribo)
Cortante nominal resistente
El menor valor de Vn = 66,620 kg + 166,541 kg + 0 = 233,161 kg
Vn = 0.25 x 210 x 100 x 86.74 + 0 = 455,385 kg
Luego Vn = 233,161 kg
Cortante resistente total
Vr = ØVn = 0.9(233,161 kg) = 209,845 kg > 200,000 Kg OK!
Refuerzo transversal mínimo
' bv s
A v ≥ 0.083 fc [mm2 ] (5.8.2.5-1)
fy
bvs
= A v ≥ 0.27 fc' [cm2 ]
fy
100( .5)
17
A v ≥ 0.27 210 cm2
4200
A v mín = 1.63 cm² < 8.00 cm² OK !
Espaciamiento máximo del refuerzo transversal (Art. 5.8.2.7)
Vu − φVp
vu = (5.8.2.9-1)
φb v d v
Vu 200,000
vu = = = 25.62 kg / cm²
φb v d v 0.9(
100)(86.74)
También:
si vu < 0.125f’c smáx= 0.8dv ≤ 60 cm (5.8.2.7-1)
si vu ≥ 0.125f’c smáx= 0.4dv ≤ 30 cm (5.8.2.7-2)
Como vu = 25.62 kg/cm² < 0.125(210 kg/cm²) = 26.25 kg/cm²
smáx= 0.8dv = 0.8(86.74 cm)= 69.39 cm
smáx= 60 cm
Luego s = 17.5 cm < smáx= 60 cm OK!](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-293-320.jpg)

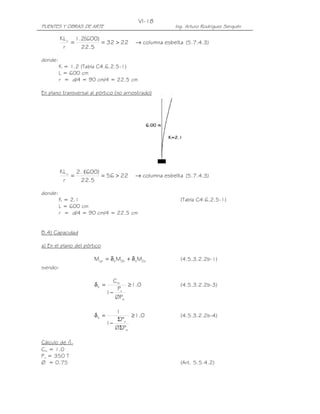



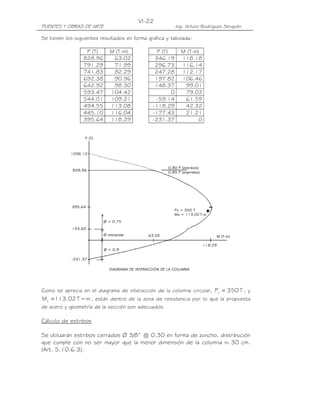




![VII-5
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
EJEMPLO VI1.1 En la viga mostrada determine el momento flector en E utilizando su
línea de influencia.
9T
2T/m
C E B D
A 4m 6m
3m 10m 2m
Solución.-
Solución.-
Después de construir la línea de influencia del momento flector en la sección E, para las
cargas dadas tenemos:
9T
2T/m
C E B D
A 4m 6m
3m 10m 2m
R
A
+4(6) =2.4m
10
+
C D
L.I. de M
E
A B
-4(2)
-3(6)=-1.8m =-0.8m
10
10
[ ]
ME = 2T / m Área + 9T(Ordenada)
ME = 2T / m[− ½ x1.8m x 3m] + 9T( +2.4m) = −16.20T − m](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-304-320.jpg)


![VII-8
PUENTES Y OBRAS DE ARTE Ing. Arturo Rodríguez Serquén
Cálculo de aP1:
Tramo AB (0 ≤ X ≤ 6):
1 X
aP1(EI) = R A ' X − X(0.4X)
2 3
0.2 3
aP1(EI) = 5.6X − X
3
Tramo BC (6 ≤ X ≤ 10):
Tomando momentos hacia la derecha:
1 ( − X)
10
aP1(EI) = R C ' ( − X) −
10 ( − X)( − X)0.6
10 10
2 3
aP1(EI) = 6.4( − X) − 0.1( − X) 3
10 10
d) Para la construcción de RB tenemos:
Tabulación de valores:
Tramo AB (0 ≤ X ≤ 6): X (m) RB
0 0
1 0.2 3
RB = (5.6X − X ) 1 0.289
19.2 3
2 0.556
3 0.781
Tramo BC (6 ≤ X ≤ 10):
4 0.944
1 5 1.024
RB =
19.2
[
6.4( − X) − 0.1 − X) 3
10 (
10 ] 6 1.000
7 0.859
8 0.625
9 0.328
10 0
Gráfica:](https://image.slidesharecdn.com/puenteslrfd-ingarturorodrguez-130321104945-phpapp01/85/Puentes-LRFD-Ing-Arturo-Rodriguez-307-320.jpg)