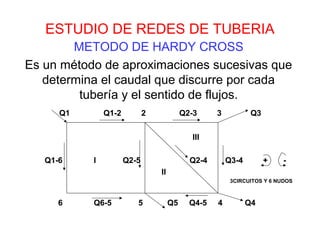
El método de Hardy Cross es un método de aproximaciones sucesivas para determinar los caudales en cada tubería y el sentido de flujo en una red de tuberías. Se basa en cumplir la ecuación de continuidad en cada nudo y que la suma algebraica de las pérdidas de carga sea cero en cada circuito. Comienza con una distribución inicial de caudales aproximada y calcula nuevos caudales iterativamente hasta que el cambio entre iteraciones sea menor al 1% del caudal.

1. ESTUDIO DE REDES DE TUBERIA
METODO DE HARDY CROSS
Es un método de aproximaciones sucesivas que
determina el caudal que discurre por cada
tubería y el sentido de flujos.
Q1 Q1-2 2 Q2-3 3 Q3
III
Q1-6 I Q2-5 Q2-4 Q3-4 + -
II
3CIRCUITOS Y 6 NUDOS
6 Q6-5 5 Q5 Q4-5 4 Q4

2. METODO DE HARDY CROSS
1.- La ecuación de la continuidad se debe cumplir en cada
momento.
Qingreso = Qsalida
Q = Q3 + Q4 + Q5
En el nudo 1 : Q = Q1-2 + Q1-6
2.- La suma algebraica de perdida de cargas de cada
circuito debe ser cero.
hf1-2 + hf2-5 + hf6-5 + hf1-6 = 0
Donde: hf = kQn
n=2 (si Darcy)
n = 1.85 (si Hazen y Williams)

3. METODO DE HARDY CROSS
PROCEDIMIENTO:
Como una aproximación se asume una
distribución de caudales iniciales en cada tramo.
Qo = Caudal inicial aprox. En un tramo (asumir)
hfo = kQon (perdida inicial aproximado)
Q = Qo + ΔQ = siguiente caudal aproximado
hf = k(Qo+ ΔQ)n = Siguiente perdida aprox.
Si : ΔQ < 1%Q Q será el caudal verdadero
de lo contrario se sigue los mismos pasos
tomando como nuevo Qo = Q hasta que
ΔQ < 1%Q y alrededor de cada circuito Σhf =0 y
Q en tramos comunes serán iguales.

4. METODO DE HARDY CROSS
Σhf = Σho + ΔQ Σ(nhfo/Qo)
Donde: ΔQ = - Σhfo/(nΣhfo/Qo)
hf = 1745155.28LQ1.85/(C1.85 D4.85) Hazen y
Williams
hf = 0.0826 fLQ2/D5 Darcy

5. Aplicación

6. Aplicación