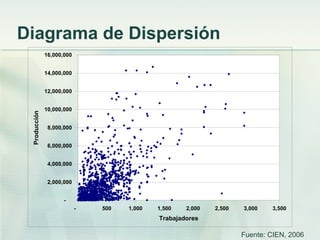
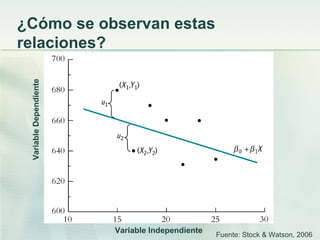
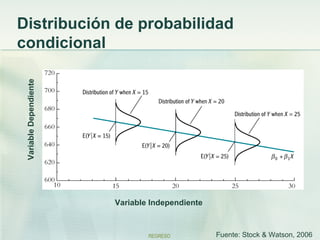
La econometría es la ciencia que prueba teorías económicas mediante el análisis de datos reales, predice valores de variables económicas y vincula modelos económicos con información del mundo real. Utiliza métodos estadísticos como la regresión lineal para estimar parámetros que miden las relaciones funcionales entre variables económicas, como la producción y el empleo. Estas estimaciones ayudan a responder preguntas sobre el impacto de políticas públicas.

1. ¿Qué es econometría?
Introducción a la Econometría
Sesión 1
10/Enero/2007

2. ¿Qué es Econometría?
 “Ciencia” que…
• ¿Prueba teorías económicas?
• ¿Predice o proyecta los valores de
variables económicas?
• ¿Es un proceso que acopla la
información real a los modelos
económicos?
• ¿Hace recomendaciones de política
pública?
Stock & Watson (2003)

3. Preguntas a responder
 ¿Cuál es la elasticidad - precio del
petróleo?
 ¿Reducir el tamaño de la clase puede
mejorar el rendimiento en las clases?
 ¿El impuesto al tabaco realmente
disminuye la cantidad de fumadores?
 ¿Cuál es el beneficio marginal en el
S.O.M. por cada quetzal invertido en
publicidad?

4. Necesidad por respuestas concretas
 ¿Cuál sería el cambio en los ingresos por
un incremento de X% en el precio?
 ¿Qué efecto tendría sobre la producción el
incremento del 5% del salario mínimo?
 ¿Qué impuesto recauda más: un 12% de
IVA a la vivienda o un 2% de impuesto
sobre las transacciones?
 ¿Realmente son nuestras exportaciones
competitivas a nivel Latinoamericano?

5. A la luz de la teoría económica
 La calidad del análisis dependerá de la
pregunta a resolver.
• Destacar las relaciones funcionales entre las
variables económicas de interés.
 Inicio de la investigación econométrica:
• Especificación del modelo
o Ejemplo: Producción = Y[L(+)]

6. Diagrama de Dispersión
16,000,000
14,000,000
12,000,000
10,000,000
Producción
8,000,000
6,000,000
4,000,000
2,000,000
-
- 500 1,000 1,500 2,000 2,500 3,000 3,500
Trabajadores
Fuente: CIEN, 2006

7. Especificación del Modelo
Yi = β 0 + β1 ⋅ x1 + u1
(Método de regresión lineal con un regresor)
 Esta relación define el interés del estudio.
 Variable Dependiente (Yi) .
o Está en función de otras variables.
 Variable Independiente (Xi).
o Explica los cambios observados en las variables
dependientes.

8. Especificación del Modelo
Yi = β 0 + β1 ⋅ x1 + u1
(Método de regresión lineal con un regresor)
 Interpretación de los parámetros (βi).
 β0: intercepto.
o ¿Cuál es el valor de Y cuando X es cero?
o E(Y|x=0)
 β1: pendiente.
o ¿Cuál es el cambio marginal en Y cuando cambia X?
o ¿Cuánto varía Y si X cambia en una unidad?
o Cambio en Y/ Cambio en X

9. Especificación del Modelo
Yi = β 0 + β1 ⋅ x1 + u1
(Método de regresión lineal con un regresor)
 Interpretación del error (u1)
 Diferencia entre una relación estocástica y una
determinista.
 Término de disturbios y se justifica por:
o Omisión de factores (al azar) que inciden sobre Y.
o Errores en la medición.
o La imposibilidad de relaciones humanas determinísticas.

10. ¿Cómo se observan estas
relaciones?
Variable Dependiente
Variable Independiente
Fuente: Stock & Watson, 2006

11. ¿Cómo estimar la función
especificada?
Función poblacional (teórica) a estimar:
Yi = β 0 + β1 ⋅ x1 + ui
Función estimada a partir de datos observados:
Yi = b0 + b1 ⋅ x1 + e1
Y =Y ˆ +e
i i i

12. Método de Mínimos Cuadrados
Ordinarios (OLS)
Estima los parámetros minimizando la sumatoria de
errores cuadrados
n n
∑ e =∑ (Yi − Yi ) 2
i =1
2
i
ˆ
i =1
Supuestos:
• E(u|xi)=0
• (Xi,Yi) están idéntica e independientemente
distribuidas.
• (Xi, ui) tienen un cuarto momento finito y distinto a
cero.

13. Fórmulas de parámetros estimados
por OLS
Intercepto:
b0 = Y − b1 ⋅ x
Pendiente:
n n n
∑ x ⋅ Y − Y ⋅ ∑ x ∑ ( x − x )(Y − Y )
i i i i i
S xy
b1 = i =1
n n
i =1
= i =1
n
=
S x2
∑ xi2 − x ⋅ ∑ xi
i =1 i =1
∑ ( xi − x ) 2
i =1
*La última fórmula se alcanza multiplicando el numerador y denominador por n-1.
REGRESO

14. Distribución de probabilidad
condicional
Variable Dependiente
Variable Independiente
REGRESO Fuente: Stock & Watson, 2006

15. Reflexión final
 Al realizar estimaciones utilizando OLS se
minimiza el error cuadrático, pero:
 No significa que los residuos sean pequeños.
 No da fianza de la bondad de ajuste de la
regresión.
 No garantiza una relación real entre la
variable dependiente y la variable
independiente.
 No asegura que se cumplan sus supuestos.