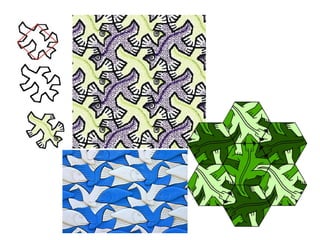
Este documento describe las redes modulares y cómo se pueden usar en el diseño. Las redes modulares organizan el espacio bidimensional y tridimensional a través de módulos repetidos y formas geométricas como triángulos, cuadrados y hexágonos. Artistas como M.C. Escher y Piet Mondrian han utilizado redes modulares en sus obras a través de transformaciones, superposiciones y deformaciones de las formas geométricas.