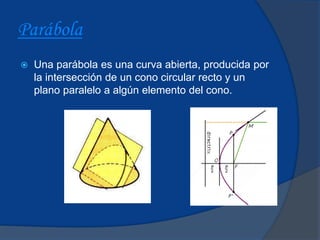
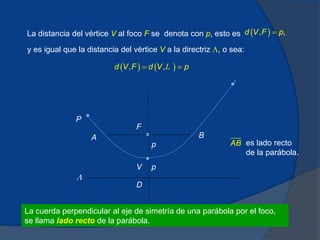
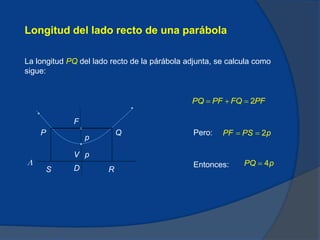
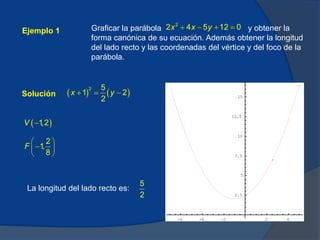
El documento presenta información sobre parábolas, incluyendo su definición como el lugar geométrico de puntos equidistantes de una recta y un punto fijo, y cómo se construye una parábola conociendo el foco y la directriz. También cubre fórmulas para calcular la longitud del lado recto y coordenadas del vértice y foco. Se incluyen ejemplos resueltos y breve historia sobre el descubrimiento de las secciones cónicas.

1. CONALEP
IZTAPALAPA V
(211)
Unidad de Operación Desconcentrada
para el Distrito Federal

2. La parábola

3. La parábola
Contenido
 Presentación
 Objetivo
 Un breve repaso
 La parábola
Clase Muestra

4. Presentación Academia de Matemáticas
Periodo 21213
Enrique Trejo
Rodriguez
Carmen
Rodriguez
Lemus
Jonathan
Zambrano Cruz
Manuel Rangel
Carrillo
Luis Eduardo
Santiago Chávez

5. Objetivo
Al finalizar seremos capaces de
definir que es una parábola,
cuales son sus principales
formulas y donde lo podemos
aplicar.

6. Un breve repaso

7. La línea recta
 Recordaras varias definiciones de la línea recta dadas en
sus estudios anteriores, siendo la más común la que se
expresa diciendo que una recta es la distancia más corta
entre dos puntos. Pero esta definición se apoya en el
significado del término distancia.
P1 P2

8. La línea recta
 También llamamos línea recta al lugar geométrico de los
puntos tales que tornados dos puntos diferentes
cualesquiera P1 (x1 , y1) y P2 (x2 , y2) del Iugar, el valor de la
pendiente por medio de la formula:
𝑚 =
𝑦1 − 𝑦2
𝑥1 − 𝑥2
, 𝑥1 ≠ 𝑥2

9. La línea recta
Forma general de la ecuación de una
recta.
En donde ya sea A o B debe ser diferente
de cero y C puede o no ser igual a cero.
La ecuación se llama la forma general de
la ecuación de una recta.

10. La circunferencia
 Definición. Circunferencia es el lugar geométrico
de un punto que se mueve en un plano de tal
manera que se conserva siempre a una distancia
constante de un punto fijo de ese plano.
 El punto fijo se llama centro de la circunferencia,
y la distancia constante se llama radio.
Radio
Punto Fijo
Circunferencia

11. La circunferencia
 Teorema 1. La circunferencia cuyo
centro es el punto (h, k) y cuyo radio es
la constante r, tiene por ecuación:
 Corolario . La circunferencia de centro
en el origen y radio r tiene por ecuación

12. La circunferencia
 Teorema 2: La ecuación x2 + y2 + Dx +
Ey + F una circunferencia de radio
diferente de cero, solamente si
D2 + E2 - 4 F > 0

13. La parábola

14. Parábola
 Una parábola es una curva abierta, producida por
la intersección de un cono circular recto y un
plano paralelo a algún elemento del cono.

15. Una parábola se define como el lugar geométrico de todos los puntos
equidistantes de una recta y un punto fijos. El punto fijo se llama foco y
la recta fija se llama directriz de la parábola.
X
B
V
L
P
F
directriz
Foco
q
p
Y
D
n
m
1. Trazar
2. Bisecar
3. Unir F con
cualquier X en L
4. Trazar la mediatriz
m de
5. Trazar por
X. Se obtiene P en
6. Para obtener más
puntos, se repite lo
hecho en 3, 4 y 5
con cualquier otro
punto de L.

FD L
FD
FX

n L
m n

Conocidos el foco y la directriz, la parábola se construye como sigue:

16. ¿Qué sucede con la parábola si la distancia del foco a la directriz crece?
¿Qué sucede con la parábola, si la distancia del foco a la directriz decrece?
¿Es la mediatriz m de tangente a la parábola?
FX
¿Cuál es el lugar geométrico de los puntos medios de los segmentos
determinados al unir el foco con los puntos de la directriz?
La parábola se abre
La parábola se cierra
Sí
Es la paralela a la directriz por el vértice de la parábola

17. La distancia del vértice V al foco F se denota con p, esto es    ,
,
d V F p
V
L
P
F
D
p
p
A B
y es igual que la distancia del vértice V a la directriz L, o sea:
   
 
, ,
d V F d V p
L
La cuerda perpendicular al eje de simetría de una parábola por el foco,
se llama lado recto de la parábola.
AB es lado recto
de la parábola.

18. Si el eje de simetría de la parábola es vertical y su vértice coincide con el
origen, las coordenadas del foco son la ecuación de la directriz
es Por lo que, si es cualquier punto de la parábola
entonces se satisfacen las siguientes relaciones:
 ,
0,
F p
 
,
P x y
.
y p
 
   

, ,
d P d P F
L
   
2 2
2 2
0
0 1
y p
x y p

   

 
2
2
x y p y p
   
   
2 2
2
x y p y p
   
2
4
x py

La parábola abre hacia arriba si
La parábola abre hacia abajo si
0
p 
0
p 
O
L
F(0,p)
Q
p
p
x
y
y = p
 
,
P x y

19. Si el eje de simetría de la parábola es vertical y su vértice es las
coordenadas del foco son y la ecuación de la directriz es
Por lo que, si es cualquier punto de la parábola,
entonces se satisfacen las siguientes relaciones:
 
, ,
F h k p

.
y k p
   
,
P x y
 
, ,
V h k
   
, ,
d P F d P
 L
   
2 2
2 2
0 1
y k p
x h y k p
 
    

   
2 2
x h y k p y k p
      
     
2 2 2
x h y k p y k p
      
   
2
4
x h p y k
  
La parábola abre hacia arriba si
La parábola abre hacia abajo si
0
p 
0
p 
0
Q
p
x
 
,
F h k p
  
,
P x y
p
y
h
k
y = k - p

20. Longitud del lado recto de una parábola
La longitud PQ del lado recto de la párábola adjunta, se calcula como
sigue:
V
L
F
D
p
p
S R
P Q
   2
PQ PF FQ PF
Pero:   2
PF PS p
Entonces:  4
PQ p

21. Ejemplo 1
Solución
Graficar la parábola y obtener la
forma canónica de su ecuación. Además obtener la longitud
del lado recto y las coordenadas del vértice y del foco de la
parábola.
   
2
2 4 5 12 0
x x y
   
  
2 5
1 2
2
x y
 
1
,2
V
 

 
 
2
1,
8
F
La longitud del lado recto es:
5
2
-6 -4 -2 2 4
2.5
5
7.5
10
12.5
15

22. La calzada de un puente parabólico está sobre el lado recto
de una parábola, cuyo vértice está a 20 m de altura por arriba
de la calzada. Tomando como eje x a la horizontal que define
a la calzada, y como eje y al eje de simetría de la parábola, y
si los extremos del lado recto están cada uno a 60 m del foco,
determinar la gráfica y la ecuación de la parábola, y las
coordenadas de los puntos de anclaje del puente en las orillas
de la Bahía .
Ejemplo 2
Solución  
2
80 20
x y
  
Los puntos de anclaje del
puente son:
 
60, 25
P  
 
60, 25
Q 
Q
P

23. Si el eje de simetría de la parábola es horizontal y su vértice coincide con
el origen, las coordenadas del foco son la ecuación de la directriz
es Por lo que, si es cualquier punto de la parábola
entonces se satisfacen las siguientes relaciones:
 
0 ,
,
F p
 
,
P x y
.
x p
 
   
, ,
d P F d P
 L
 
2 2
2 2
1 0
x p
x p y

  

 
2 2
x p y y p
   
   
2 2
2
x p y y p
   
2
4
y px

La parábola abre hacia la derecha si
La parábola abre hacia la izquierda si
0
p 
0
p 
O
L
F(p,0)
Q
p p
x
y
x
=

p
 
,
P x y

24. Si el eje de simetría de la parábola es horizontal y su vértice es las
coordenadas del foco son y la ecuación de la directriz es
Por lo que, si es cualquier punto de la parábola, entonces
se satisfacen las siguientes relaciones:
 ,
,
F h p k

.
x h p
   
,
P x y
 
, ,
V h k
   

, ,
d P d P F
L
   
2 2
2 2
1 0
x h p
x h p y k
 
    

   
2 2
x h p y k x p
     
     
2 2 2
x h p y k x h p
      
   
2
4
y k p x h
  
La parábola abre hacia la derecha si
La parábola abre hacia la izquierda si
0
p 
0
p 
0
Q
p p
x
 
,
F h p k

 
,
P x y
x = h  p
y
h
k
L

25. Ejemplo 3
Solución
Graficar la parábola y obtener la forma
canónica de su ecuación. Además obtener la longitud del lado
recto y las coordenadas del vértice y del foco de la parábola.
2
8 6 7 0
y x y
   
   
2
3 8 2
y x
   
 
2, 3
V 
 
0, 3
F 
La longitud del lado recto es: 8
-5 -4 -3 -2 -1 1 2
-10
-8
-6
-4
-2
2
4

26. y
x
0
La calzada de un puente parabólico está sobre el lado recto de una
parábola, cuyo vértice está a 20 m de altura por arriba de la calzada.
Tomando como eje x a la horizontal que define la calzada, y como eje y al
eje de simetría de la parábola, y si los extremos del lado recto están cada
uno a 60 m del foco, se puede determinar la ecuación de la parábola y las
coordenadas de los puntos de anclaje del puente en las orillas de la Bahía .

27. Curvas con Historia
 Se dice que Menaechmus fue el que descubrió las secciones
cónicas y que fue el primero en enseñar que las parábolas,
hipérbolas y elipses eran obtenidas al cortar un cono en un
plano no paralelo a su base.
 Apollonius describió las cónicas como las curvas formadas en un
plano.
 Apollonius de Perga fue otro matemático que estudio las cónicas,
su trabajo tuvo una gran influencia en el estudio de las
matemáticas, también descubrió que las cónicas se podían
clasificar en tres tipos a los que dio el nombre de: elipses,
hipérbolas y parábolas.
 Apolonio demostró que las curvas cónicas tienen muchas
propiedades interesantes: las llamadas propiedades de reflexión.

28.  En la actualidad esta propiedad se utiliza para los
radares, las antenas de televisión y espejos solares. La
propiedad análoga, que nos dice que un rayo que parte
del foco se refleja paralelamente al eje sirve para que los
faros de los automóviles concentren el haz en
la dirección de la carretera o para estufas.
Propiedades de Reflexión

29. Las aplicaciones principales de las parábolas
incluyen su como reflectores
de luz y ondas de radio.
Los rayos originados en el foco de la parábola se
reflejan hacia afuera de la parábola, en líneas
paralelas al eje de la parábola. Aun más
el tiempo que tarda en llegar cualquier rayo al
foco a una recta paralela a la directriz de la
parábola y por lo tanto estas propiedades se
utilizan en linternas, faros de automóviles,
en antenas de transmisión de microondas.
PROPIEDADES
REFLECTORAS

30. ASTRONOMIA
El físico italiano Galileo (1564-1642) descubrió la
ley que gobierna el movimiento de los cuerpos
sobre la superficie de la Tierra: La velocidad de
caída de los cuerpos no depende de su masa y es
directamente proporcional al tiempo. Esto implica
que si lanzamos un objeto con cierta inclinación
hacia arriba la trayectoria seguida es una parábola.
ORBITA
DE LOS
COMETAS
A cierta distancia del Sol, existe una velocidad umbral llamada velocidad
de escape, v. Cuando un cometa tiene una velocidad igual o mayor que v,
escapa del sistema solar . Si su velocidad es menor permanece dentro
del campo gravitacional del Sol.
Trayectoria del cometa: Elíptica si su velocidad es menos que v.
Hiperbólica si es mayor que v. Parabólica si es igual a v.
En los dos últimos casos, el cometa se acerca al Sol una sola vez y se
retira al espacio para nunca volver (solo se considera interacción entre
2 cuerpos, Sol-cometa)

31. Evaluación
 ¿Cual es el nombre que se da a las graficas de una ecuación
cuadrática?
 En una ecuación cuadrática, ¿cómo podemos determinar el
vértice de su grafica?
 Elabora tres funciones cuadráticas y explica por que las
funciones son cuadráticas. Grafícalas.
 Dadas las siguientes funciones, determinar las coordenadas
de su vértice y si la parábola abrirá hacia arriba o hacia abajo.
 .