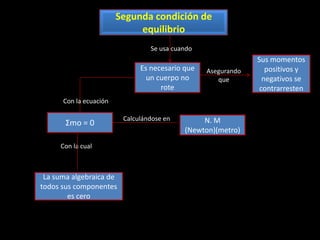
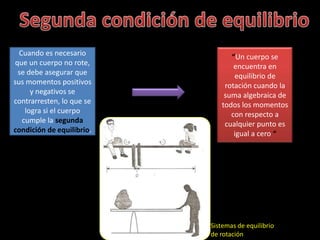
El documento presenta información sobre la segunda condición de equilibrio de rotación. Explica que un cuerpo está en equilibrio de rotación cuando la suma algebraica de todos los momentos con respecto a cualquier punto es igual a cero. Proporciona la ecuación ΣMo= 0 y ejemplos de su aplicación para calcular fuerzas desconocidas.

2. Centro de Estudios Tecnológicos
Industrial y de Servicios 109
Tema: Segunda condición de equilibrio
Integrantes:
González Rosales Luis Andrés
Mar Cruz Juan Carlos
Muñoz Fuentes Pedro Pablo
Ramírez Romero Orlando
Sandoval García Carlos
Grado: 6° Sem Grupo: “L”
Materia: Temas de Física
Profesor: Ing. Ernesto Yañez Rivera
Especialidad: Informática

3. Cuando es necesario “Un cuerpo se
que un cuerpo no rote, encuentra en
se debe asegurar que equilibrio de
sus momentos positivos rotación cuando la
y negativos se suma algebraica de
contrarresten, lo que se todos los momentos
logra si el cuerpo con respecto a
cumple la segunda cualquier punto es
condición de equilibrio. igual a cero “
Sistemas de equilibrio
de rotación

4. Ecuación de la segunda condición de equilibrio:
ΣMo= 0
Sumatoria de todos los momentos que actúan N. m
sobre el cuerpo (Newton)(metro)
-La suma vectorial de las fuerzas que -La suma vectorial de
actúan sobre un cuerpo debe ser cero. momentos en torsión
debe ser cero

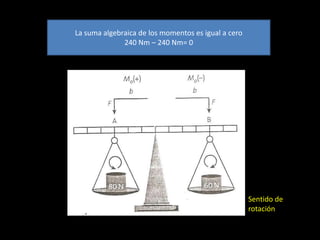
5. Ejemplo:
Para mantener en equilibrio de rotación una balanza que
soporta pesos diferentes en cada uno de sus platillos, se
colocan a diferentes distancias del eje de rotación.
1.-Para mantener el
equilibrio, los pesos
deberán A B
encontrarse a
distintas distancias
del centro, de tal
manera que se
anulen los efectos
de rotación que se
presenten en cada
extremo.
2.- Esto se consigue
colocándolos a 3 y 4
m. para comprobar , 3.- En el punto A, el 4.-El punto B tiene un
se cuantifican los momento positivo valor de momento
momentos alrededor tiene un valor de negativo de
del eje de rotación. [(80N)(3m)= +240Nm] [(60N)(4m)= -240 Nm]

6. La suma algebraica de los momentos es igual a cero
240 Nm – 240 Nm= 0
Sentido de
rotación

7. Se usa una polea de dos ejes para soportar pesos de 15 y 20
N, respectivamente. Si el diámetro interior es de 0.04 m y el
exterior de 0.08m, ¿qué valor tendrá el efecto de giro
resultante en el eje de la polea?
.

8. Consideraciones hechas:
•El primer momento es positivo al girar en sentido contrario
de las manecillas de reloj.
•El segundo momento es negativo, ya que el efecto de
rotación es en el mismo sentido del movimiento de las
manecillas del reloj.
.
•En los datos se proporciona el diámetro , así que el brazo de
la palanca es la mitad, o sea la distancia medida desde el
centro hasta donde se encuentra la fuerza.
•Se calcula la suma de todos los momentos, ya que se pide el
efecto neto de giro sobre el eje central de la polea.
•La suma de los momentos es algebraica, es decir,
considerando su signo.
•El resultado indica que el efecto neto es un giro con igual
sentido al de las manecillas del reloj.

9. Ante el peso que sostienen los soportes de una estructura de acero,
éstos reaccionan con determinanda fuerza. Utilizando la segunda
condición de equilibrio, calcula el valor de los pesos desconocidos.
2. Incógnita
F y F=?N
2 3
3. Ecuación
Σmo= 0
•Al ser un cuerpo extendido que se encuentra en equilibrio de rotación, se debe
cumplir que la sumatoria de los momentos respecto a cualquier punto de éste
sea cero.
•Es un sistema de fuerzas coplanar paralelo que presenta dos incógnitas y en el
cual el peso de la viga se considera despreciable.
•Se aplica la sumatoria de los momentos en unos de los sitios donde se
encuentra una de las incógnitas, así que al aplicarse al punto A, la ecuación que
se obtine comprende sólo la otra variable desconocida, F3 .

11. Segunda condición de
equilibrio
Se usa cuando
Sus momentos
Es necesario que Asegurando positivos y
un cuerpo no que negativos se
rote contrarresten
Con la ecuación
Calculándose en N. M
Σmo = 0
(Newton)(metro)
Con la cual
La suma algebraica de
todos sus componentes
es cero