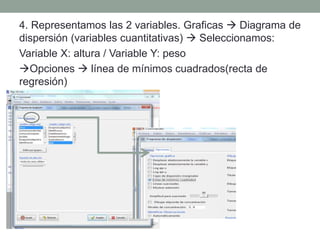
Este documento resume los pasos para analizar la relación entre las variables altura y peso utilizando datos reales. Muestra gráficas que indican que la altura y el peso no siguen una distribución normal, por lo que se usa la prueba no paramétrica de Spearman. La correlación de Spearman entre altura y peso es de 0.6224114, lo que sugiere una relación moderada entre las variables.

1. SEMINARIO 8
ANÁLISIS BIVARIADO
Carmen Vivas López
Estadística y TICs. Virgen del Rocío
Subgrupo16

2. Ejercicio Blog
• Determinar si existe relación y cómo de fuerte es entre
las variables altura y peso.
1. Cargamos conjunto de datos: activossalud

3. 2. Gráficas de comparación de cuantiles.
Seleccionamos la variable altura y observamos
En opciones  Normal
(para ver normalidad)
Vemos si sigue normalidad
la variable altura.
No sigue la normalidad
puesto que hay puntos que
no están dentro de los
intervalos de confianza la
distribución no sigue la
normalidad.

4. 3. Y ahora igual con el peso…
 Tampoco sigue la normalidad
 Por lo tanto usaremos test no paramétrico:
Rho de Spearman

5. 4. Representamos las 2 variables. Graficas  Diagrama de
dispersión (variables cuantitativas)  Seleccionamos:
Variable X: altura / Variable Y: peso
Opciones  línea de mínimos cuadrados(recta de
regresión)

6. 5. A simple vista podemos observar que las variables
parecen tener relación.

7. 6. Averiguamos si es así:
Resúmenes estadísticos matriz de correlaciones
aplicamos Spearman (cuantitativa)  obtenemos valor
del estadístico
La correlación altura-peso tiene un
valor de 0.6224114
En la práctica un valor por debajo
del 0.80 se considera que las
variables NO están correlacionadas