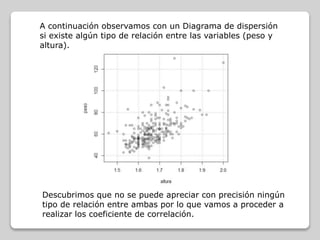
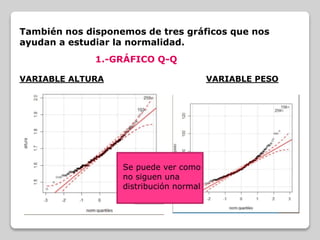
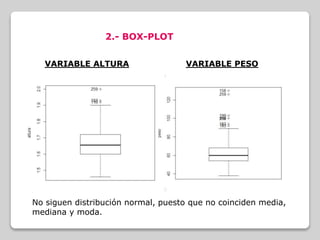
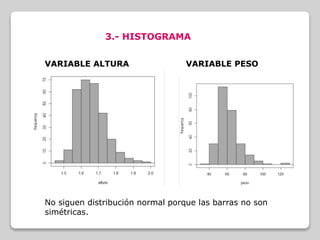
Este documento analiza la relación entre las variables de altura y peso en un conjunto de datos de salud. No siguen una distribución normal, por lo que se usa el coeficiente de correlación de Spearman. Los resultados muestran una correlación positiva moderada entre altura y peso.

1. Análisis bivariado con
variables cuantitativas.
Normalidad y linealidad. Diagrama de dispersión.
Coeficientes de correlación de Pearson y Rho de Spearman.
Ana Bautista Garrote
Grupo A, subgrupo 1
ENFERMERIA (Macarena)

2. EJERCICIO
Determina si existe relación
entre las variables altura y
peso del fichero de datos
“activos en salud” y si existe
determina cómo de fuerte es.

3. -En primer lugar, debemos cargar el
conjunto de datos de “Activos en
salud” en R Commander.
-En segundo lugar comprobamos si
las dos variables cuantitativas siguen
o no una distribución normal:
 Pearson: si sigue una distribución
normal.
 Rho de Spearman: si no sigue una
distribución normal.

4. A continuación observamos con un Diagrama de dispersión
si existe algún tipo de relación entre las variables (peso y
altura).
Descubrimos que no se puede apreciar con precisión ningún
tipo de relación entre ambas por lo que vamos a proceder a
realizar los coeficiente de correlación.

5. Primero vamos a estudiar si existe
distribución normal en las variables (peso y
altura)
Para ello, vamos a utilizar el Test de Shapiro
Wilk, y pasamos a formular las dos hipótesis
correspondientes:
 Hipótesis nula: la variable (peso o altura) sí
sigue una distribución normal.
 Hipótesis alternativa: la variable (peso o altura)
no sigue una distribución normal

6. Al realizar el Test de Shapiro Wilk obtenemos estos
resultados:
VARIABLE PESO
Observamos que el p-valor
es menor que 0,05, y
sabiendo que el error que
podíamos cometer es
menor del que en un
principio estábamos
dispuestos a asumir….
…aceptamos la
hipótesis
alternativa: la
variable no sigue una
distribución normal
VARIABLE ALTURA

7. También nos disponemos de tres gráficos que nos
ayudan a estudiar la normalidad.
1.-GRÁFICO Q-Q
VARIABLE PESOVARIABLE ALTURA
Se puede ver como
no siguen una
distribución normal

8. 2.- BOX-PLOT
VARIABLE PESOVARIABLE ALTURA
No siguen distribución normal, puesto que no coinciden media,
mediana y moda.

9. 3.- HISTOGRAMA
VARIABLE PESOVARIABLE ALTURA
No siguen distribución normal porque las barras no son
simétricas.

10. Para finalizar, al no seguir una
distribución normal las variables,
debemos utilizar el coeficiente de Test
de Spearman.
Para ello, antes establecemos las dos
hipótesis correspondientes:
 Hipótesis nula: Existe correlación entre
peso y altura (Rho entre -1 y 1)
 Hipótesis alternativa: No existe
correlación entre peso y altura (Rho=0)

11. RESULTADO:
Vemos que Rho es distinto de 0. por lo que podemos decir según
las hipótesis formuladas anteriormente, que aceptamos la
hipótesis nula (existe correlación entre peso y altura).
Se trata de una correlación positiva puesto que 0,622 está
alejado del 0 y más cerca del 1.