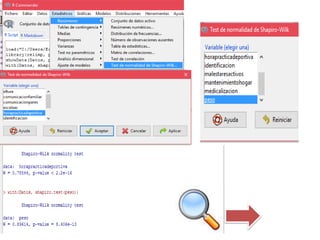
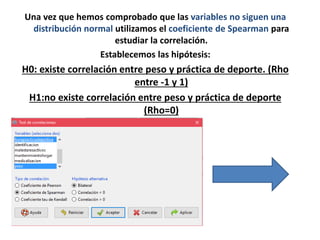
Este documento resume los pasos para calcular la correlación entre dos variables cuantitativas. Primero, se eligen las variables peso y horas de práctica deportiva. Luego, se usa la prueba de Shapiro-Wilk para determinar que ninguna variable sigue una distribución normal, por lo que se utiliza el coeficiente de Spearman. Los resultados muestran una correlación débil pero existente entre peso y horas de práctica deportiva.

1. EJERCICIO TEMA
•Elige dos variables de la matriz de datos.
La que queráis pero deberás justificarla.
Recuerda que tienes que hacer la prueba
de normalidad para decidir el estadístico
de correlación que tienes que utilizar.
• Comenta los resultados.
•Represéntalos gráficamente.

2. Correlación: grado o fuerza de la relación o asociación entre
dos variables cuantitativas. Dos variables se relacionan
cuando las mediciones de una variable cambian
simultáneamente o proporcionalmente con las medidas de
la otra.
Para su cálculo es necesario conocer si las variables siguen o no
una distribución normal, ya que dependiendo de esto
usaremos uno u otro coeficiente:
• R de Pearson (las dos siguen la distribución normal)
• Rho de Spearman (una de los dos no sigue una distribución
normal)

3. En primer lugar elegimos dos variables, teniendo en cuenta que para
poder calcular la correlación estas han de ser variables
cuantitativas. Escogemos la variable peso y horas de práctica
deportiva.
A través del test de normalidad de Shapiro Wilks comprobamos si las
variables siguen o no una distribución normal. Para ello,
establecemos las hipótesis:
H0: La variable sigue una distribución normal.
H1: La variable no sigue una distribución normal

5. El p-valor en ambos casos, que representa el error que cometeríamos si
aceptásemos la hipótesis alternativa, es inferior al que estamos dispuestos a
asumir (0.05) por lo tanto, se acepta la hipótesis alternativa en las dos
variables, es decir, ninguna de ellas sigue una distribución normal.

6. Una vez que hemos comprobado que las variables no siguen una
distribución normal utilizamos el coeficiente de Spearman para
estudiar la correlación.
Establecemos las hipótesis:
H0: existe correlación entre peso y práctica de deporte. (Rho
entre -1 y 1)
H1:no existe correlación entre peso y práctica de deporte
(Rho=0)

7. El valor de rho es distinto de 0, por lo tanto, podemos decir que existe
correlación entre las variables, sin embargo, esta es débil puesto que el valor
se encuentra muy próximo a 0

8. Lo representamos con una gráfica de dispersión para observarlo con
mayor exactitud: