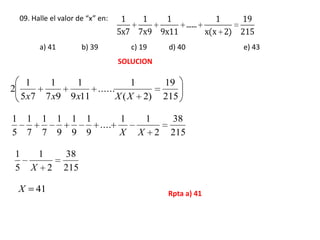
El documento contiene 16 problemas de matemáticas que involucran cálculos de sumas, progresiones aritméticas y geométricas, y términos enésimos. Se pide determinar valores, razones y sumas. La mayoría de los problemas se resuelven aplicando fórmulas matemáticas apropiadas a cada caso.

1. 01. Calcular la suma de los 100 primeros términos de la siguiente sucesión:
1, 2, 3, -4, 5, 6, 7, -8, 9, 10, 11, -12, ….
a) 4500 b) 9900 c) 3000 d) 2450 e) 8500
SOLUCION
Por lo tanto quedaría
Rpta d) 2450

2. SOLUCION
02. Calcular:
a) 45 b) 58 c) 77 d) 50 e) 85
1 8 27 64 1000
S ...
5 10 15 20 50
10
1000
....
4
64
3
27
2
8
1)(5 S
100....16941)(5 S
5S=
5S=385
S=77
Rpta c) 77

3. 03. Calcular:
a) 1/2 b) 6/125 c) 4/5 d) 1/8 e) 4/25
1 1 1 1 1
...
10x7 14x9 18x11 22x23 246x125
SOLUCION
125123
1
....
119
1
97
1
75
1
)(2
xxxx
S
125
1
123
1
....
11
1
9
1
9
1
7
1
7
1
5
1
)(4 S
125
1
5
1
)(4 S
125
24
)(4 S
125
6
S Rpta b) 6/125

4. 04. La suma de los 6 primeros términos de una progresión geométrica es igual a 9
veces la suma de los 3 primeros términos. Determine el valor de la razón.
a) 1 b) 2 c) 3 d) 4 e) 5
SOLUCION
.........:. 654321 TTTTTTGP
.........:. 5432
1 TxqTxqTxqTxqTxqTGP
1
11
q
qT
S
n
1
1
9
1
1 3
1
6
1
q
qT
x
q
qT
191 36
qq
33
98 qq
2q
Rpta b) 2

5. 05. Hallar la suma de los 20 primeros sumandos de: 5 + 9 + 15 + 23 +….
a) 3140 b) 3240 c) 3340 d) 3410 e) 3540
SOLUCION
32
nnTn
+ +
222
20......21 + 20......21 + 203x
6
412120 xx
2
2120x 60++
602102870
3140 Rpta a) 3140

6. 06. Si una sucesión está definida por:
Determine la suma de los 20 primeros términos de dicha progresión.
a) 89180 b) 75800 c) 88080 d) 80180 e) 73872
SOLUCION
742 3
nnTn
+ +
)20......21(2 333 + )20......21(4 + 207x
2
2
2120
2
x
2
2120
4
x
x 140++
14084088200
89180 Rpta a) 89180

7. 07. Determinar el valor de la suma de las cifras de:
a) 12 b) 13 c) 14 d) 15 e) 16
(5) (6) (7)
13sumandos
S 11 22 33 ...

SOLUCION
  
oster
S
min13
......3624146 nnTn 52
+
)13......21( 222
)13......21(5+
2
1413
5
6
271413 x
x
xx 1274
Rpta c) 14144721cifrasdesuma

8. 08. Calcular: S = 2x3 + 6x4 + 12x5 + …+272x18
a) 23356 b) 23756 c) 23256 d) 23852 e) 23842
181716.....654543432321 xxxxxxxxxxS
SOLUCION
4
321 nnnn
S
4
19181716
S
23256S
Rpta c) 23256
Recordar
Reemplazando

9. 09. Halle el valor de “x” en:
a) 41 b) 39 c) 19 d) 40 e) 43
1 1 1 1 19
......
5x7 7x9 9x11 x(x 2) 215
SOLUCION
215
19
)2(
1
......
119
1
97
1
75
1
2
XXxxx
215
38
2
11
....
9
1
9
1
9
1
7
1
7
1
5
1
XX
215
38
2
1
5
1
X
41X Rpta a) 41

10. 10. La suma de los 20 primeros números enteros consecutivos es 410. Calcular la suma de
los 20 números enteros consecutivos siguientes.
a) 930 b) 810 c) 1200 d) 900 e) 950
SOLUCION
Sea los 20 primeros números
consecutivos:
19...........21 aaaa
n
TT
S n
2
1
20
2
19
410
aa
19241 a
19241 a
11a
Suma de los 20numeros siguientes
n
TT
S n
2
1
20
2
39)20( aa
S
10)592( aS
810S
Rpta b) 810
39...........2120 aaa

11. 11. Calcular: S = 1x4 + 2x5 + 3x6 + …+20x23
a) 2400 b) 2880 c) 3480 d) 2650 e) 3500
SOLUCION
32020.........333322311S
32020.......333322311 2222
xxxxS
20...321320.......321 2222
S
2
2120
3
6
412120 xxx
S
6302870S
3500S
Rpta e) 3500

12. 12. Calcular:
a) 5 b) 4 c) 3 d) 3 e) 1
2 3
1 1 1
S 1 2 3 4 ....
2 2 2
SOLUCION
q
T
S
1
1
Recordar
..........
2
4
2
3
2
2
2
1
3210
S
..........
2
5
2
4
2
3
222 321
xS
-
........
2
1
2
1
2
1
12 321
S
Reemplazando
2
1
1
2
S 4S Rpta b) 4

13. 13. El primer término de una Progresión aritmética creciente de razón par menor que 4 es
igual a “a+b” y el ab-esimo término es 55. Hallar la suma de los ba primeros términos.
a) 3016 b) 3015 c) 3012 d) 3020 e) 3025
SOLUCION
Recordar rnTTn 11 rnTTn 0ó
2155 abba
222055 baba
232155 ba
ba 32157
52 ba
Reemplazando
  
ostermin52
................1197
252552T 10952T
n
TT
S n
2
1
52
2
1097
S
3016S
Rpta a) 3016
Suma de los primeros términosba

14. 14. Halle la suma de los 20 primeros términos de: -2; 0; 0; 0; 2; 8;…...
a) 7730 b) 7570 c) 7700 d) 7750 e) 7755
SOLUCION
;........8;2;0;0;0;2
2 0 0 2 6
-2 0 2 4
2 2 2
CCCC
nnnn
nT
1
3
1
2
1
1
1
0
2222
CCCC
nnnn
n
n
nT 4321
1
2222
!!1
!
kn
n
C
n
k
Recordar el termino enésimo:
Recordar la suma de términos:
Recordar :
Remplazando convenientemente:
CCCC
n
n
nT
20
4
20
3
20
2
20
1
20
1
2222
24
17181920
2
6
181920
2
2
1920
2
1
20
2
xxxxxx
xS
7750S
Rpta d) 7750

15. 15. Calcular:
a) 21/2 b) 23/2 c) 23/3 d) 13/3 e) 20/3
2
n
n 1
7n 2
E
3
SOLUCION
.....................
243
177
81
114
27
65
9
30
3
9
E
....................
81
63
27
49
9
35
3
21
92xE
.....................
81
177
27
114
9
65
3
30
93xE
-
....................
27
63
9
49
3
35
21276xE
-
....................
27
14
9
14
3
14
394xE
Recordar
q
T
S
1
1
3/11
3/14
394xE
2
23
E
Rpta d) 7750

16. 16. Calcular “S”, en la siguiente serie de 10 términos.
a) 23/2 b) 10/3 c) 20/3 d) 23/6 e) 1/3
2n n 2n 1
S ...
30 35 126 21
SOLUCION
21
1
...................
633515
nnn
S
2321
...................
977553 x
n
x
n
x
n
x
n
S 23n
)
2321
1
...................
97
1
75
1
53
1
(23
xxxx
S
23
1
3
1
232S
3
10
S Rpta b) 10/3