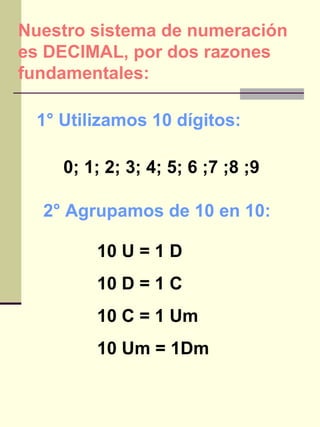
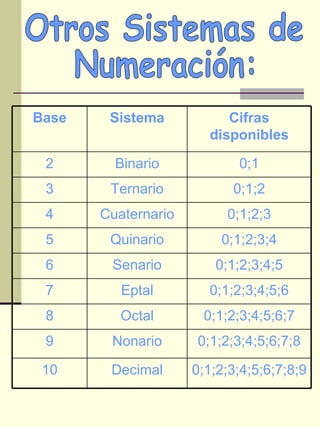
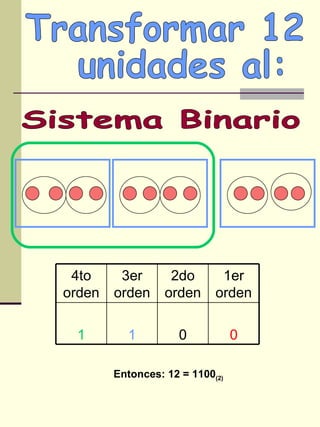
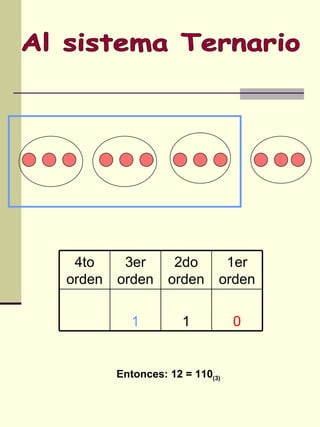
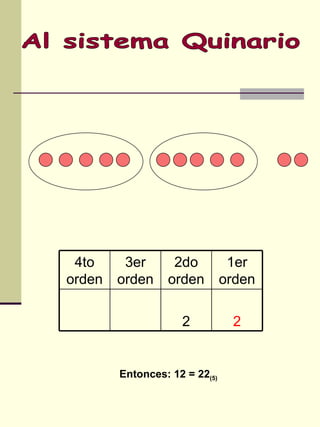
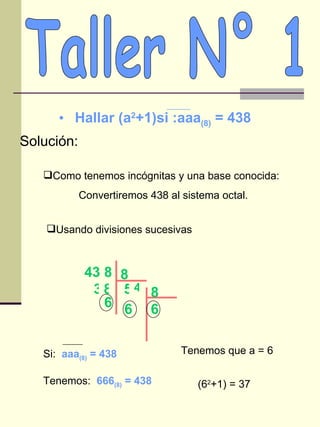
El documento explica los sistemas de numeración, incluyendo el sistema decimal que usamos y otros sistemas como el binario, ternario y octal. Describe cómo descomponer números en diferentes posiciones y bases y cómo convertir entre sistemas de numeración. Incluye ejemplos de resolución de problemas usando diferentes sistemas.

1. SISTEMAS DE NUMERACIÓN

2. Nuestro sistema de numeración es DECIMAL, por dos razones fundamentales: 1° Utilizamos 10 dígitos: 0; 1; 2; 3; 4; 5; 6 ;7 ;8 ;9 2° Agrupamos de 10 en 10: 10 U = 1 D 10 D = 1 C 10 C = 1 Um 10 Um = 1Dm

3. Descomposición de un número: 215085 Según el nombre de la posición: Según el valor de la posición: Según el valor por unidades: 215085= 2Cm + 1Dm + 5Um + 8D + 5U 215085= 200000 + 10000 + 5000 + 80+ 5 215085= 2x100000 + 1x10000 + 5x1000 + 8x10+ 5x1 Ahora como la vamos a descomponer:(Polinómicamente) 215085= 2x10 5 + 1x10 4 + 5x10 3 + 8x10 1 + 5x10 0

4. Otros Sistemas de Numeración: 0;1;2;3;4;5;6;7;8;9 Decimal 10 0;1;2;3;4;5;6;7;8 Nonario 9 0;1;2;3;4;5;6;7 Octal 8 0;1;2;3;4;5;6 Eptal 7 0;1;2;3;4;5 Senario 6 0;1;2;3;4 Quinario 5 0;1;2;3 Cuaternario 4 0;1;2 Ternario 3 0;1 Binario 2 Cifras disponibles Sistema Base

5. Transformar 12 unidades al: Sistema Binario Entonces: 12 = 1100 (2) 0 0 1 1 1er orden 2do orden 3er orden 4to orden

6. Al sistema Ternario Entonces: 12 = 110 (3) 0 1 1 1er orden 2do orden 3er orden 4to orden

7. Al sistema Quinario Entonces: 12 = 22 (5) 2 2 1er orden 2do orden 3er orden 4to orden

8. Descomponer: 35896 35896= 3x10 4 + 5x10 3 + 8x10 2 + 9x10 1 + 6x10 0 4 000 150 008 4 000 150 008= 4x10 9 + 1x10 5 + 5x10 4 + 8x10 0 20 054 869 20 054 869= 2x10 7 + 5x10 4 + 4x10 3 + 8x10 2 + 6x10 1 + 9x10 0 100 009 300 205 100 009 300 205= 1x10 11 + 9x10 6 + 3x10 5 + 2x10 2 + 5x10 0

9. Escribir en el cuaderno de práctica

10. Taller N° 1 Hallar x si: 64 (x) = 52 Expresarlo en el sistema más usado por nosotros: El sistema decimal, Solución: Usando la descomposición poli nómica 64 (x) = 52 6(x) + 4 = 52 6x =52-4 6x=48 x = 8

11. Taller N° 1 Hallar (a 2 +1)si :aaa (8) = 438 Como tenemos incógnitas y una base conocida: Convertiremos 438 al sistema octal. Solución: Usando divisiones sucesivas 43 8 8 5 3 6 8 6 6 8 4 Si: aaa (8) = 438 Tenemos: 666 (8) = 438 Tenemos que a = 6 (6 2 +1) = 37

12. Taller N° 1 Si: 2aa (4) = 37, hallar a Expresarlo en el sistema más usado por nosotros: El sistema decimal, Solución: Usando la descomposición poli nómica 2aa (4) = 37 2(4) 2 + a(4) + a = 37 32 + 5a = 37 5a =5 a = 1