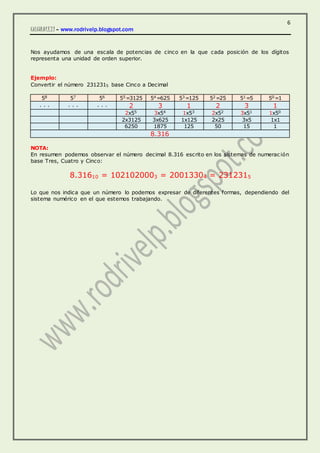
Este documento explica los sistemas de numeración base 3, 4 y 5. Describe cómo convertir números entre las bases decimal, binaria, ternaria, cuaternaria y quinternaria usando divisiones sucesivas y escalas de potencias. Como ejemplo, el número 8.316 se puede expresar como 1021020003 en base 3, 20013304 en base 4 y 2312315 en base 5.

1. Matemáticas
Grado Sexto
Sistemas de Numeración Base
3, 4 y 5
Docente
Rodrigo Velasco Palomino
www.rodrivelp.blogspot.com
Institución Educativa Técnico Industrial
I.E.T.I
Popayán Cauca
Colombia

2. 2
CALCULOI.E.T.I – www.rodrivelp.blogspot.com
TABLA DE CONTENIDO
SISTEMAS DE NUMERACIÓN
BASE 3, 4 y 5
1 Conceptos básicos de Sistemas de Numeración
2 Sistema de Numeración Base 3
3 Sistema de Numeración Base 4
4 Sistema de Numeración Base 5
5 Taller
10. Bibliografía
11. Webgrafía

3. 3
CALCULOI.E.T.I – www.rodrivelp.blogspot.com
SISTEMAS DE NUMERACIÓN
Los sistemas de numeración estudiados a continuación son de tipo posicional, e decir sistemas
en que se fundamentan en que cada dígito utilizado depende tanto del símbolo usado como de
la posición que ocupa dentro del número.
SISTEMA DE NUMERACIÓN BASE 3
Se denomina Base Tres porque se hacen agrupaciones de tres en tres para la construcción de
cualquier número y utiliza tres dígitos diferentes en su sistema: el cero, el uno y el dos:
{0, 1, 2}
DECIMAL A BASE TRES POR DIVISIONES SUCESIVAS
Este método consiste en dividir sucesivamente cada uno de los cocientes por tres en el que los
residuos representan al número en base tres.
Ejemplo:
Convertir el número 8.316 de base diez a base tres.
Solución:
Se divide el número dado por tres y cada uno de los resultados en el cociente se siguen dividiendo
sucesivamente por tres hasta que el último cociente sea menor de tres; los residuos obtenidos
hacen parte de la solución pedida los cuales se deben escribir de derecha a izquierda como lo
indica la flecha del ejemplo.
|
BASE TRES A DECIMAL USANDO POTENCIAS DE TRES
Nos ayudamos de una escala de potencias de tres en la que cada posición de los dígitos
representa una unidad de orden superior.
Ejemplo:
Convertir el número 1021020003 base Tres a Decimal
Solución:

4. 4
CALCULOI.E.T.I – www.rodrivelp.blogspot.com
En la escala desarrollamos cada una de las potencias y las multiplicamos por su respectivo dígito
y al final sumamos todos los valores para obtener así el número decimal pedido.
38=6561 37=2187 36=729 35=243 34=81 33=27 32=9 31=3 30=1
1 0 2 1 0 2 0 0 0
1x38 0x37 2x36 1x35 0x34 2x33 0x32 0x31 0x30
1x6561 0x2187 2x729 1x243 0x81 2x27 0x9 0x3 0x1
6561 0 1458 243 0 54 0 0 0
8.316
SISTEMA DE NUMERACIÓN BASE 4
Se denomina Base Cuatro porque se hacen agrupaciones de cuatro en cuatro para la construcción
de cualquier número y utiliza cuatro dígitos diferentes en su sistema: el cero, el uno, el dos y el
tres:
{0, 1, 2, 3}
DECIMAL A BASE CUATRO POR DIVISIONES SUCESIVAS
Este método consiste en dividir sucesivamente cada uno de los cocientes por cuatro en el que
los residuos representan al número en base cuatro.
Ejemplo:
Convertir el número 8.316 de base diez a base cuatro.
Solución:
Se divide el número dado por cuatro y cada uno de los resultados en el cociente se siguen
dividiendo sucesivamente por cuatro hasta que el último cociente sea menor de cuatro; los
residuos obtenidos hacen parte de la solución pedida los cuales se deben escribir de derecha a
izquierda como lo indica la flecha del ejemplo.

5. 5
CALCULOI.E.T.I – www.rodrivelp.blogspot.com
BASE CUATRO A DECIMAL USANDO POTENCIAS DE CUATRO
Nos ayudamos de una escala de potencias de cuatro en la que cada posición de los dígitos
representa una unidad de orden superior.
Ejemplo:
Convertir el número 20013304 base Cuatro a Decimal
48 47 46=4096 45=1024 44=256 43=64 42=16 41=4 40=1
. . . . . . 2 0 0 1 3 3 0
2x46 0x45 0x44 1x43 3x42 3x41 0x40
2x4096 0x1024 0x256 1x64 3x16 3x4 0
8192 0 0 64 48 12 0
8.316
SISTEMA DE NUMERACIÓN BASE 5
Se denomina Base Cuatro porque se hacen agrupaciones de cinco en cinco para la construcción
de cualquier número y utiliza cinco dígitos diferentes en su sistema: el cero, el uno, el dos, el
tres y el cuatro:
{0, 1, 2, 3, 4}
DECIMAL A BASE CINCO POR DIVISIONES SUCESIVAS
Este método consiste en dividir sucesivamente cada uno de los cocientes por cinco en el que los
residuos representan al número en base cuatro.
Ejemplo:
Convertir el número 8.316 de base diez a base cinco.
Solución:
Se divide el número dado por cinco y cada uno de los resultados en el cociente se siguen
dividiendo sucesivamente por cinco hasta que el último cociente sea menor de cinco; los residuos
obtenidos hacen parte de la solución pedida los cuales se deben escribir de derecha a izquierda
como lo indica la flecha del siguiente ejemplo.
BASE CINCO A DECIMAL USANDO POTENCIAS DE CINCO

6. 6
CALCULOI.E.T.I – www.rodrivelp.blogspot.com
Nos ayudamos de una escala de potencias de cinco en la que cada posición de los dígitos
representa una unidad de orden superior.
Ejemplo:
Convertir el número 2312315 base Cinco a Decimal
58 57 56 55=3125 54=625 53=125 52=25 51=5 50=1
. . . . . . . . . 2 3 1 2 3 1
2x55 3x54 1x53 2x52 3x51 1x50
2x3125 3x625 1x125 2x25 3x5 1x1
6250 1875 125 50 15 1
8.316
NOTA:
En resumen podemos observar el número decimal 8.316 escrito en los sistemas de numerac ión
base Tres, Cuatro y Cinco:
8.31610 = 1021020003 = 20013304 = 2312315
Lo que nos indica que un número lo podemos expresar de diferentes formas, dependiendo del
sistema numérico en el que estemos trabajando.