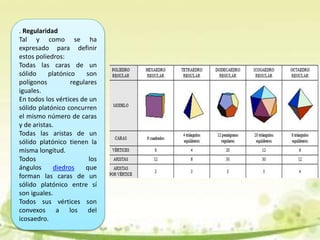
Este documento describe los sólidos platónicos, incluyendo su historia, propiedades y características. Platón asoció cada uno de los cuatro elementos con un poliedro regular: fuego al tetraedro, aire al octaedro, agua al icosaedro y tierra al cubo. El quinto poliedro regular, el dodecaedro, lo asoció al Universo. Los sólidos platónicos tienen caras regulares iguales, el mismo número de caras en cada vértice, y exhiben varias simetrías como simetría puntual

1. SÓLIDOS PLATÓNICOS
Santiago Juanías
Juliana Tamayo
Gustavo Novoa

2. HISTORIA
•
Dentro de las infinitas formas
poliédricas que existen hay unas que,
por sus simetrías, han ejercido siempre
una gran atracción sobre los hombres.
Se trata de los poliedros regulares,
cuyas caras son polígonos regulares
iguales entre sí y en cuyos vértices
concurren el mismo número de
caras. Platón, en su obra Timaeus,
asoció cada uno de los cuatro
elementos que según los griegos
formaban el Universo Fuego, aire, agua
y tierra a un poliedro: fuego al tetraedro,
aire al octaedro, agua al icosaedro y
tierra al hexaedro o cubo. Finalmente
asoció el último poliedro regular, el
dodecaedro, al Universo. Por este
motivo estos poliedros reciben el
nombre de sólidos platónicos.

3. PRE-CONCEPTOS
En geometría, una arista
son las líneas que
conforman una figura
geométria y los vértices
son los puntos que unen
las aristas

4. . Regularidad
Tal y como se ha
expresado para definir
estos poliedros:
Todas las caras de un
sólido platónico son
polígonos regulares
iguales.
En todos los vértices de un
sólido platónico concurren
el mismo número de caras
y de aristas.
Todas las aristas de un
sólido platónico tienen la
misma longitud.
Todos los
ángulos diedros que
forman las caras de un
sólido platónico entre sí
son iguales.
Todos sus vértices son
convexos a los del
icosaedro.

5. •
Conjugación
Si se traza un poliedro empleando como
vértices los centros de las caras de un sólido
platónico se obtiene otro sólido platónico,
llamado conjugado del primero, con tantos
vértices como caras tenía el sólido inicial, y
el mismo número de aristas. El poliedro
conjugado de un dodecaedro es un
icosaedro, y viceversa; el de un cubo es un
octaedro; y poliedro conjugado de un
tetraedro es otro tetraedro.
Ecuación intrínseca
El Teorema de poliedros de Euler expresa
una cualidad topológica de los poliedros
convexos, al margen de sus medidas y
formas, y de modo especial de los poliedros
regulares.7 Enuncia que el número de caras
de un poliedro platónico más el número de
sus vértices es igual al número de sus aristas
más dos, mediante la siguiente ecuación:

6. Algunas propiedades son:
Convexidad
Regularidad: Todas las caras, los
ángulos y los lados del mismo sean
iguales, en todos los vértices
concurren el mismo número de caras
y vértices.
Estos sólidos tiene muchas simetrías a
las cuales podríamos reducir en:
Simetría Puntual: Que para cada
sólido platónico existe un punto
central (que equidista de todas
las caras) del poliedro, este será
el centro de simetría.
Simetría Axial: Tienen además
varios ejes de simetría, pero todo
de ellos pasan por el centro de
simetría.
Simetría de plano: Presentan
simetrías respecto a los planos.
Contienen el centro de simetría y
a combinaciones de los ejes.

7. https://es.wikipedia.org/wiki/S%C3%B3lidos_plat%C3
%B3nicos
https://es.wikipedia.org/wiki/S%C3%B3lidos_plat%C3
%B3nicos
http://mcnenipopo.blogspot.com.co/