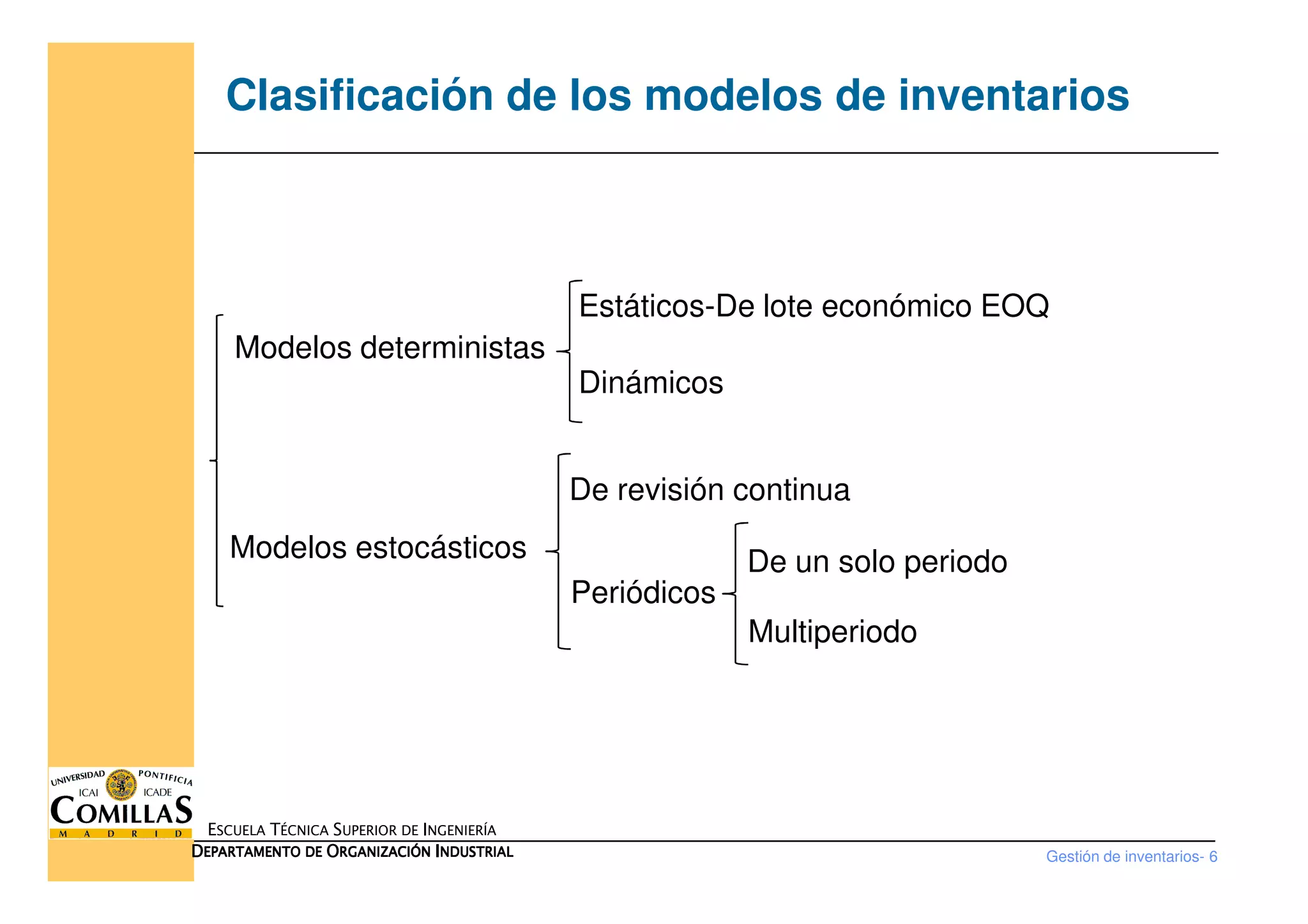
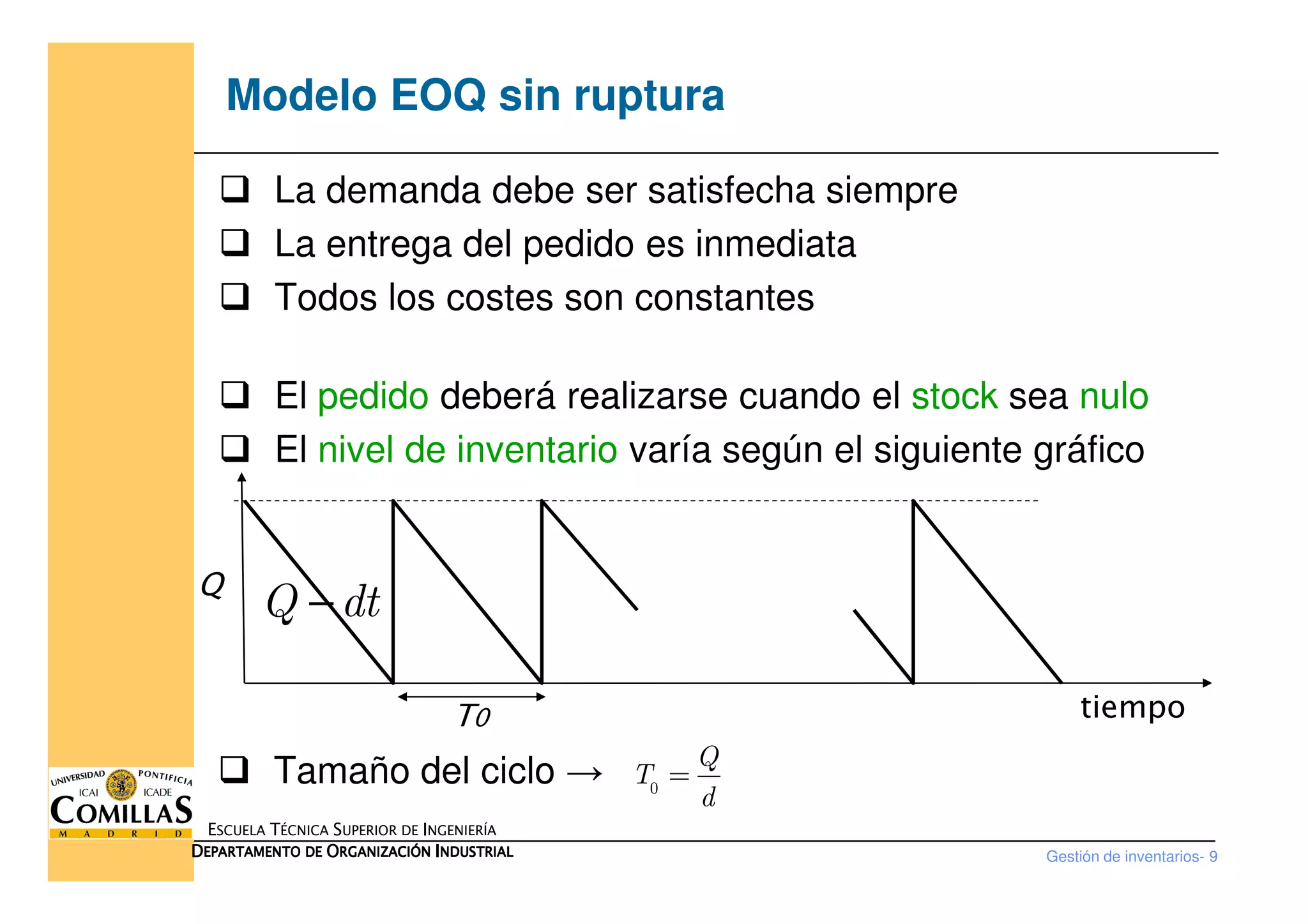
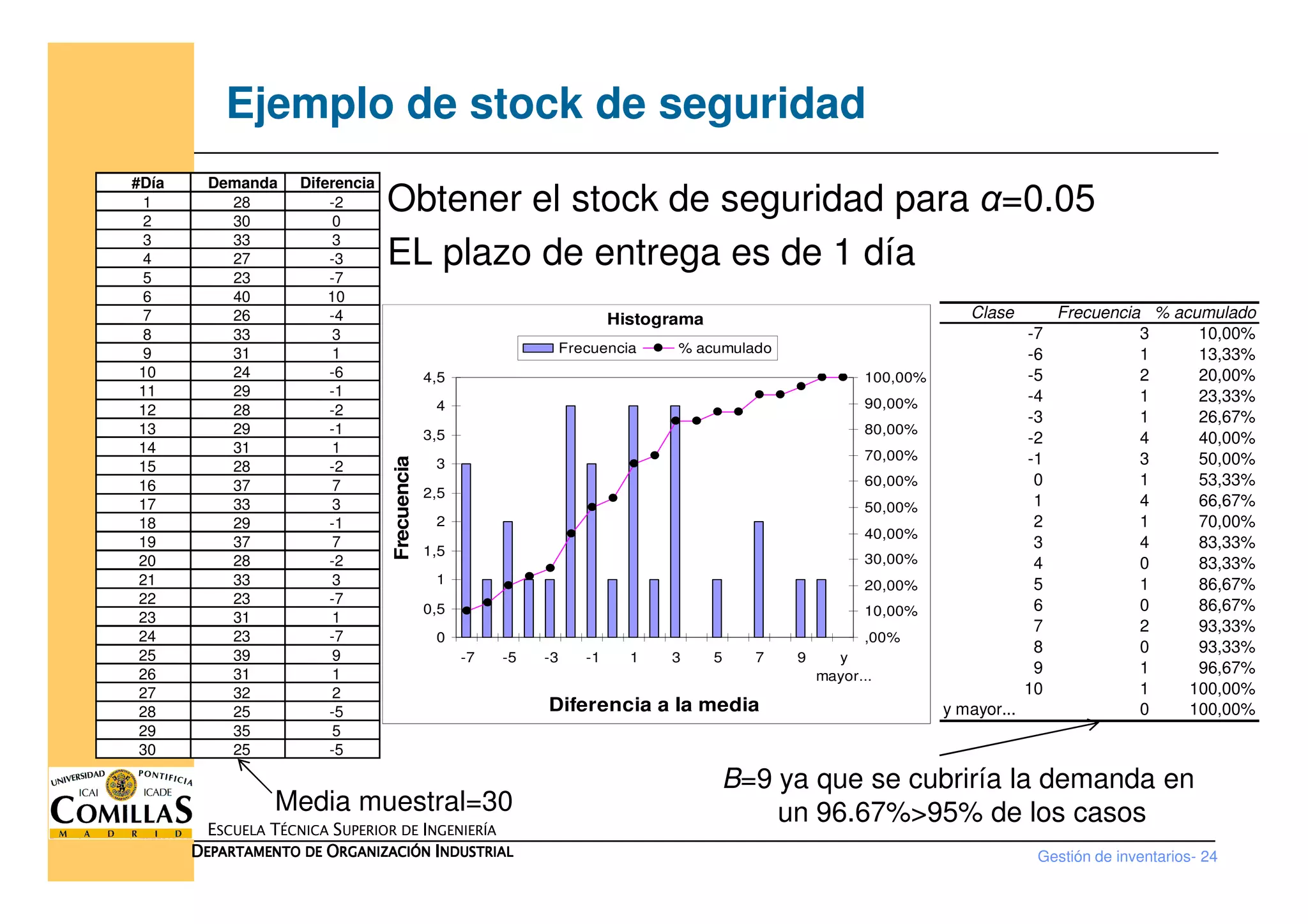
Este documento trata sobre la gestión de inventarios. Explica los diferentes tipos de costes asociados a los inventarios, como el coste de compra, orden, almacenamiento y ruptura. También describe los diferentes modelos de inventarios, como el modelo de lote económico (EOQ), que minimiza los costes totales fijando el tamaño óptimo de pedido. El documento proporciona las fórmulas para calcular el tamaño óptimo de pedido en los diferentes modelos, como el modelo EOQ básico, con ruptura y con ent